Constant de la gravitació

La constant de la gravitació, també anomenada constant gravitacional, constant de la gravitació universal o constant de Newton, denotada , és la constant física fonamental que determina la intensitat de la interacció gravitacional entre masses[notes 1] que actualment té el valor següent:[1]
La notació moderna de la llei de Newton que implica fou introduïda a la dècada de 1890 pel físic anglès Charles V. Boys. La primera mesura implícita amb una precisió d'aproximadament l'1% s'atribueix a Henry Cavendish en un experiment de 1798.[notes 2]
La constant és la constant de proporcionalitat que apareix en la llei de la gravitació universal d'Isaac Newton i en la teoria de la relativitat general d'Einstein. A la llei de Newton, és la constant de proporcionalitat que connecta la força gravitatòria entre dos cossos amb el producte de les seves masses i la quadrat invers de la seva distància. Això és equivalent a dir que dues masses d'1 quilogram cada una, separades una distància d'1 metre, s'atrauen l'una a l'altra amb una força gravitacional aproximada de 6,67 × 10–11 newtons. A les equacions de camp d'Einstein, quantifica la relació entre la geometria de l'espai-temps i el tensor d'energia i impuls (també conegut com a Tensor d'energia-moment).
Història
[modifica]Teoria de la gravitació de Newton
[modifica]
Newton descobrí que l'atracció entre dues masses és directament proporcional al producte de les seves masses i inversament proporcional al quadrat de la distància que separa els seus centres. La formulació moderna d'aquesta llei de gravitació universal és:
on és la intensitat de la força d'atracció, i les masses dels dos cossos que experimenten aquesta interacció, la distància que separa els centres dels cossos i és la constant de proporcionalitat. Aquesta constant no fou mai emprada per Newton perquè ell només emprà relacions de forces i no realitzà cap intent de calcular valors d'aquestes forces.

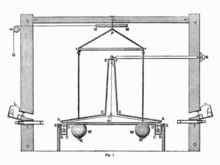
L'experiment de Cavendish
[modifica]L'experiment de Cavendish és un experiment dut a terme entre 1797 i 1798 pel científic britànic Henry Cavendish (1731-1810) amb l'objectiu de determinar la densitat mitjana de la Terra. La determinació d'aquesta densitat permeté després calcular la seva massa a partir del radi de la Terra i la massa de la Lluna, el Sol i la resta de planetes del sistema solar. De la densitat de la Terra es determinà posteriorment el valor de la constant de gravitació universal amb el radi de la Terra i el valor del camp gravitatori a la superfície de terrestre , aplicant que la massa de la Terra és igual a la seva densitat pel volum de la Terra :[2]
Cavendish millorà un dispositiu, anomenat balança de torsió, dissenyat al voltant del 1783 per John Michell (1724-1793) que morí sense poder completar l'experiment. El resultat obtingut per Cavendish fou que la densitat mitjana de la Terra era 5,437 g/cm3 o 5 437 kg/m3, només un 1,4 % menor que el valor ara acceptat, 5,515 g/cm3,[2] i que implica un valor de = 6,759 × 10–11 m3 kg–1 s–2:[3][4]
Determinacions posteriors a Cavendish
[modifica]Després de l'experiment realitzat per Cavendish altres científics repetiren l'experiment amb el mateix muntatge introduint millores. A partir de mitjan segle xix els experiments es portaven a cap ja amb l'objectiu de determinar la constant de la gravitació, , i no la densitat de la Terra. En destaquen:
L'alemany Ferdinand Reich (1799-1882) repetí la mesura de la densitat de la Terra amb una balança molt similar a l'emprada per Cavendish i obtingué nous valors de la densitat mitjana de la Terra, ρ = 5,49 g/cm³ el 1837 ( = 6,69 × 10–11 m3 kg–1 s–2) i ρ = 5,58 g/cm³ el 1852 ( = 6,59 × 10–11 m3 kg–1 s–2). L'astrònom anglès Francis Baily (1774-1844) repetí l'experiment de la balança de torsió i aconseguí el 1842 un valor de ρ = 5,67 g/cm³ ( = 6,48 × 10–11 m3 kg–1 s–2).[5]
| Determinacions de la constant G amb balances de torsió | ||
| Autor | Mètode | G·10-11 (N·m2/kg2) |
| Cavendish, 1798 | Desviació | 6,759 |
| Boys, 1895 | Desviació | 6,658 |
| Braun, 1897 | Període i desviació | 6,658 |
| Heyl, 1930 | Període, amb or | 6,678 |
| Període amb platí | 6,664 | |
| Període amb vidre | 6,674 | |
| Heyl i Chrzanowski, 1942 | Període | 6,676 |
| Període | 6,668 | |
| Luther i Towler, 1982 | Període | 6,6726 |
Els físics francesos Marie Alfred Cornu (1841-1902) i Jean-Baptistin Baille (1841-1918) trobaren el 1873 valors de ρ que oscil·len entre 5,50 i 5,56 g/cm³ ( = 6,68 × 10–11 m3 kg–1 s–2 — 6,61 × 10–11 m3 kg–1 s–2).[6]
El 1895, el físic anglès Charles Vernon Boys (1855-1944) modificà l'instrument original de Michell i Cavendish miniaturitzant-lo a 1/18 parts, substituint el fil de torsió, originalment de ferro, per fines fibres de quars, de 0,002 mm de diàmetre. Aquesta innovació li permeté utilitzar masses d'or menors (m = 2,7 g; M = 7,5 kg) i una distància de separació també menor, 15 cm,[7] alhora que controlà millor les variacions de temperatura i les variacions del pendent del sòl. També separà verticalment 6 polzades la posició de les parelles d'esferes amb l'objectiu de reduir l'efecte de l'esfera grossa de l'altre parell i disposà un mirall al braç que reflectia un raig de llum el qual permetia determinar mitjançant un telescopi el petit angle de desviació.[8] Els seus mesuraments donaren el valor = 6,658 × 10–11 m3 kg–1 s–2.[9]

El 1897, el físic alemany Karl Ferdinand Braun (1950-1918) millorà la balança de torsió tancant-la dins un recipient on n'extragué l'aire, així evità els corrents d'aire que afecten l'oscil·lació. També emprà un nou mètode. Situà les masses grosses en línia amb les masses petites del braç, per després canviar la seva disposició 90°, mètode anomenat del període d'oscil·lació. En les posicions amb les quatre esferes alineades l'atracció gravitatòria es redueix el període d'oscil·lació i s'amplia amb les masses en les posicions creuades, més allunyades. Obtingué el valor ρ = 5,527 g/cm³, igual que Boys.
El mètode de Braun també fou utilitzat el 1930 pel físic estatunidenc Paul Renno Heyl (1872-1961) amb diferents materials (or, platí i vidre) i aconseguí un valor mitjà de (6,670±0,005) × 10–11 m3 kg–1 s–2[10] Repetí l'experiència el 1942 amb Peter Chrzanowski i aconseguiren un valor = (6,673±0,003) × 10–11 m3 kg–1 s–2 realitzant l'experiència amb diferents filferros.[11]
Finalment, Gabriel G. Luther i William R. Towler el 1982 feren servir esferes de wolframi de 10,5 kg i obtingueren un valor molt precís de = (6,6726±0,0005) × 10–11 m3 kg–1 s–2.[12][13]
La incertesa de 46 parts per milió del valor actual posa la constant gravitacional entre les constants físiques mesurades amb menys precisió, encara que les mesures més recents han millorat la precisió del valor de acceptat. La mesura de la massa del Sol també té la mateixa incertesa, ja que s'usa el valor de per calcular-la, així com la massa dels planetes;[14]
Teoria de la gravitació d'Einstein
[modifica]La teoria de la relativitat d'Albert Einstein apareix una altra constant, anomenada constant de la gravitació d'Einstein , que és definida per:
on és la velocitat de la llum al buit.
Aquesta constant és el factor de proporcionalitat entre el tensor de curvatura d'Einstein (que és una mesura de la intensitat del camp gravitatori) i el tensor d'energia-moment de la matèria que provoca el camp:
L'equivalent clàssic d'aquest últim equació és l'equació de Poisson per al potencial gravitatòria:
Notes
[modifica]- ↑ La "Constant de gravitació newtoniana" és el nom introduït per a G per Boys (2000). Ús del terme per T.E. Stern (1928) va ser citat erròniament com "la constant de gravitació de Newton" a Pure Science Reviewed for Profound and Unsophisticated Students (1930), en el que aparentment és el primer ús d'aquest terme. L'ús de la "constant de Newton" (sense especificar "gravitació" o "gravetat") és més recent, ja que "la constant de Newton" també ho era s'utilitza per al coeficient de transferència de calor a la llei de refredament de Newton, però ara s'ha convertit en força comú, p. Calmet et al, Quantum Black Holes (2013), p. 93; P. de Aquino, Beyond Standard Model Phenomenology at the LHC (2013), p. 3. El nom de "constant gravitacional de Cavendish", de vegades "constant gravitatòria de Newton-Cavendish", sembla haver estat comú entre els anys setanta i vuitanta, especialment en (traduccions de) literatura russa de l'època soviètica, p. Sagitov (1970 [1969]), Física soviètica: Uspekhi 30 (1987), Números 1–6, pàg. 342 [etc.]. La "constant de Cavendish" i la "constant gravitacional de Cavendish" també s'utilitzen a Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, "Gravitation", (1973), 1126f. L'ús col·loquial de "Gran G", a diferència de "g petita" per a l'acceleració gravitatòria data de la dècada de 1960 (R.W. Fairbridge, The encyclopedia of atmospheric sciences and astrogeology, 1967, pàg. 436; ús de la nota). de "G gran" contra "g petita" ja a la dècada de 1940 del tensor d'Einstein Gμν enfront del tensor mètric gμν, Llibres científics, mèdics i tècnics publicats als Estats Units d'Amèrica: una llista seleccionada de títols impresos amb anotacions: suplement de llibres publicats el 1945 –1948, Committee on American Scientific and Technical Bibliography National Research Council, 1950, pàg. 26).
- ↑ Cavendish va determinar el valor de G indirectament, informant un valor per a la massa de la Terra, o la densitat mitjana de la Terra, com a 5.448 g⋅cm−3.
Referències
[modifica]- ↑ "2018 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 20 May 2019.
- ↑ 2,0 2,1 Moreno, F. «Un Experimento Para Pesar El Mundo» (en castellà). Los Lagartos terribles. Apuntes, escritos y ensayos científicos, 15-07-2011. [Consulta: 23 octubre 2014].
- ↑ «Fundamental Physical Constants from NIST». [Consulta: 3 juliol 2023].
- ↑ «Lunar and Planetary Science at the NSSDCA». [Consulta: 3 juliol 2023].
- ↑ Baily, F «Experiments with the Torsion Rod for Determining the Mean Density of the Earth by Francis Baily». Mem. Roy. Astronom. Soc. [Londres], 14, 1843, pàg. 1-129 i i-ccxlvii.
- ↑ Newton, Isaac; Sir, Henry Cavendish; MacKenzie, Arthur Stanley. The Laws of Gravitation: Memoirs by Newton, Bouguer and Cavendish, Together with Abstracts of Other Important Memoirs (en anglès). Creative Media Partners, LLC, 2017-08-19, p. 125. ISBN 978-1-375-52346-2.
- ↑ Capderou, M. Handbook of Satellite Orbits: From Kepler to Gps. Springer Science & Business, 2014, p. 87. ISBN 9783319034164.
- ↑ «Background to Boys' experiment to determine G» (en anglès). Department of Physics. University of Oxford, 2011. Arxivat de l'original el 2015-09-24. [Consulta: 30 octubre 2014].
- ↑ Boys, C.V. «On the Newtonian Constant of Gravitation». Philos. Trans. Roy. Soc., A186, 1895, pàg. 1-72.
- ↑ Heyl, P.R «A redetermination of the constant of gravitation». J. Res. Nat. Bur. Stds., 29, 1930, pàg. 1-31.
- ↑ Heyl, P.R; Chrzanowski, P «A new determination of the constant of gravitation». J. Res. Nat. Bur. Stds., 29, 1942, pàg. 1-31.
- ↑ Luther, G.G.; Towler, W.R. «Redetermination of the Newtonian gravitational constant G». Phys. Rev. Lett., 48, 121, 1982, pàg. 121-3.
- ↑ Cook, A.H. «Experiments on gravitation». A: Hawking, S. W. i Israel, W.. Three Hundred Years of Gravitation. Cambridge University Press, 1989, p. 72-73. ISBN 9780521379762.
- ↑ Roche, John J. The mathematics of measurement: a critical history (en anglès). Springer, 1998, p.161. ISBN 0387915818.




















