Difusió

un procés de difusió de la ciència. Algunes partícules es dissolen en un got d'aigua. Inicialment, les partícules estan prop d'una cantonada del vidre. Si les partícules de tot aleatòriament es mouen ("difusa") per l'aigua, llavors les partícules eventualment es trobaran distribuïdes aleatòriament i de manera uniforme, i organitzada (però encara la difusió se seguirà produint, només que no hi haurà flux net).

La difusió és un dels diversos fenòmens de transport que es troben a la natura. Una de les característiques distintives és que és el resultat de barrejar o transportar massa sense la necessitat d'un moviment a l'engròs. Per tant, la difusió no s'ha de confondre amb la convecció o advecció, que són altres mecanismes de transport que utilitzen el moviment per moure les partícules d'un lloc a un altre. En llatí "diffundere" significa cap a fora.

Hi ha dues maneres d'introduir el concepte difusió: Una aproximació a partir de les lleis de Fick i la seva conseqüència matemàtica o des del punt de vista Físic, considerant un camí a l'atzar de les partícules que es mouen.

D'acord amb la llei de Fick el flux de difusió és proporcional al gradient de concentracions. El moviment és des de regions de major concentració a menys concentració. Des del punt de vista atomista, la difusió es considera com el moviment aleatori de les partícules difusores. En la difusió molecular, les molècules que es mouen són autopropulsades per energia tèrmica. Aquest passeig aleatori va ser descobert el 1827 per Robert Brown. Ara bé, el concepte de difusió és àmpliament utilitzat en la ciència: la física (difusió de partícules), la química i la biologia, la sociologia, l'economia i les finances (difusió de la gent, les idees i dels valors de preus). Pel que sembla, sempre el concepte del moviment a l'atzar en els conjunts d'individus és aplicable.

Història

En l'àmbit del temps, la difusió en sòlids es va utilitzar molt abans que es creés la teoria de la difusió. Per exemple, Plini el Vell havia descrit prèviament el procés de cimentació, que produeix acer a partir de l'element ferro (Fe) a través de la difusió del carboni. Un altre exemple és ben conegut des de fa molts segles, la difusió de colors dels vitralls o la pisa i la ceràmica xinesa.

A la ciència moderna, el primer estudi experimental sistemàtic de la difusió va ser realitzat per Thomas Graham. Va estudiar la difusió en gasos, i el fenomen principal va ser descrit per ell el 1831–1833:

«...gasos de diferent naturalesa, quan es posen en contacte, no s'ordenen d'acord a la seva densitat, el més pesat a sota i el més lleuger a dalt, sinó que es difonen espontàniament, recíprocament i per igual, entre si, i així romandre a l'estat íntim de mescla durant qualsevol període de temps.»

Les mesures de Graham van contribuir que James Clerk Maxwell derivés, el 1867, el coeficient de difusió del CO₂ a l'aire. La taxa derror és inferior al 5%.

El 1855, Adolf Fick, el demostrador d'anatomia de Zuric de 26 anys, va proposar la seva llei de difusió. Va fer servir la investigació de Graham, declarant el seu objectiu com "el desenvolupament d'una llei fonamental, per a l'operació de difusió en un sol element de l'espai". Va afirmar una analogia profunda entre la difusió i la conducció de la calor o l'electricitat, creant un formalisme similar a la Llei de Fourier per a la conducció de la calor (1822) i la Llei d'Ohm per el corrent elèctric (1827).

Robert Boyle va demostrar la difusió en sòlids al segle xvii mitjançant la penetració de zinc en una moneda de coure. Tot i això, la difusió en sòlids no es va estudiar sistemàticament fins a la segona part del segle xix. William Chandler Roberts-Austen, el conegut metal·lúrgic britànic i antic ajudant de Thomas Graham va estudiar sistemàticament la difusió en estat sòlid sobre l'exemple de l'or en el plom el 1896:

«[...] La meva llarga connexió amb les investigacions de Graham va fer que fos gairebé un deure intentar estendre el seu treball sobre la difusió de líquids als metalls.»

En 1858, Rudolf Clausius va introduir el concepte de camí lliure mitjà. Aquest mateix any, James Clerk Maxwell va desenvolupar la primera teoria atomística dels processos de transport en els gasos. La moderna teoria atomística de la difusió i del moviment brownià va ser desenvolupada per Albert Einstein, Marian Smoluchowski i Jean-Baptiste Perrin. Ludwig Boltzmann, en el desenvolupament dels antecedents atomístics dels processos de transport macroscòpics, va introduir l'equació de Boltzmann, que ha servit a les matemàtiques ia la física com a font d'idees i inquietuds sobre els processos de transport durant més de 140 anys.

En 1920-1921, George de Hevesy va mesurar la autodifusió utilitzant radioisòtops. Va estudiar l'autodifusió d'isòtops radioactius de plom al plom líquid i sòlid.

Yakov Frenkel (de vegades, Jakov/Jacob Frenkel) va proposar, i va elaborar en 1926, la idea de la difusió en vidres a través de defectes locals (vacants i àtoms de intersticial). Va concloure que el procés de difusió en la matèria condensada és un conjunt de salts elementals i interaccions quasiquímiques de partícules i defectes. Va introduir diversos mecanismes de difusió i va trobar constants de velocitat a partir de dades experimentals.

Algun temps després, Carl Wagner i Walter H. Schottky van desenvolupar encara més les idees de Frenkel sobre els mecanismes de difusió. Actualment, es reconeix universalment que els defectes atòmics són necessaris per mediar en la difusió als vidres.

Henry Eyring, amb coautors, va aplicar la seva teoria de les velocitats de reacció absolutes al model quasiquímic de difusió de Frenkel. L'analogia entre cinètica de reacció i difusió condueix a diverses versions no lineals de la llei de Fick.

Models Bàsics de Difusió

Flux de difusió

Cada model de difusió expressa el flux de difusió a través de concentracions, densitats o derivats. Flux és el vector $\mathbf {J}$., la transferència d'una quantitat física $N$ a través d'una àrea petita $\Delta S$, amb la normal $\nu$ i el temps $\Delta t$ és:

$\Delta N=(\mathbf {J} ,\nu )\Delta S\Delta t+o(\Delta S\Delta t)\,$

On $(\mathbf {J} ,\nu )$ és el producte interior i $o(...)$ és una notació. Si es fa servir la notació del vector àrea $\Delta \mathbf {S} =\nu \Delta S$ aleshores:

$\Delta N=(\mathbf {J} ,\Delta \mathbf {S} )\Delta t+o(\Delta \mathbf {S} \Delta t)\,.$

La dimensió del flux de difusió és [flux] = [quantitat] / ([temps] • [àrea]). La quantitat física difusora $N$ pot ser el nombre de partícules, la massa, energia, càrrega elèctrica, o qualsevol altra quantitat escalar extensa. Per la seva densitat, l'equació de difusió té la forma:

${\frac {\partial n}{\partial t}}=-\nabla \cdot \mathbf {J} +W\,$

On $W$ és la intensitat de qualsevol font local, com per exemple la velocitat d'una reacció química. Per l'equació de difusió, en les condicions límits del no-flux, es pot formular $(\mathbf {J} (x),\nu (x))=0$ en el límit, on $\nu$ és la normal del punt $x$ al límit.

Llei de Fick i equacions

• 1a llei de Fick: el flux de difusió és proporcional al gradient negatiu de la concentració:

$\mathbf {J} =-D\nabla n\,\;\;J_{i}=-D{\frac {\partial n}{\partial x_{i}}}\ .$

Col·lisions aleatòries de les partícules en un gas.

D és el coeficient de difusió, considerem dos gasos amb molècules del mateix diàmetre d i la massa m (autodifusió). En aquest cas, la teoria elemental significa camí lliure mitjà de difusió per al coeficient de difusió:

$D={\frac {1}{3}}\ell v_{T}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}m}}}{\frac {T^{3/2}}{Pd^{2}}}\,$

On k_B és la constant de Bolzmann T la temperatura, P la pressió, $\ell$ és el camí lliure mitjà i v_T és la velocitat tèrmica mitjana.

$\ell ={\frac {k_{\rm {B}}T}{{\sqrt {2}}\pi d^{2}P}}\,,\;\;\;v_{T}={\sqrt {\frac {8k_{\rm {B}}T}{\pi m}}}\,.$

Podem veure que el coeficient de difusió en l'aproximació recorregut lliure mitjà creix amb T com T^3/2 i disminueix amb P com 1/P. Si s'utilitza per P la llei del gas ideal P=RnT amb la concentració total de n, llavors es pot veure que per a la concentració de n donat el coeficient de difusió creix amb T com T^3/2 i per la temperatura donada, disminueix amb la concentració total com 1/n.

Donat dos gasos diferents, A i B, amb masses moleculars m_A, m_B i diàmetres moleculars d_A, d_B, l'estimació camí lliure mitjà del coeficient de difusió de A a B i B a A és:

$D_{\rm {AB}}={\frac {1}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}}}}{\sqrt {{\frac {1}{2m_{\rm {A}}}}+{\frac {1}{2m_{\rm {B}}}}}}{\frac {4T^{3/2}}{P(d_{\rm {A}}+d_{\rm {B}})^{2}}}\,$

• La corresponent equació de difusió, 2a llei de Fick és:

${\frac {\partial n(x,t)}{\partial t}}=\nabla \cdot (D\nabla n(x,t))=D\Delta n(x,t)\,$

On $\Delta$, és l'operador de Laplace:

$\Delta n(x,t)=\sum _{i}{\frac {\partial ^{2}n(x,t)}{\partial x_{i}^{2}}}\ .$

Equació d'Onsager per difusió i termodifusió de multicomponents

Les lleis de Fick de la difusió descriuen una barreja en un medi. La concentració d'aquesta barreja ha de ser petita i el seu gradient també. la força motriu en la difusió en la primera llei de Fick és l'antigradient de la concentració $-\nabla n$.

El 1931, Lars Onsager va incloure el procés de transport de multi omponents en el context general per equilibris no lineals de la termodinàmica. Per al transport de multicomponents,

$\mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,$

On $\mathbf {J} _{i}$ és el flux de la quantitat física i (component) i $X_{j}$ és la força termodinàmica j. Les forces termodinàmiques dels processos de transport van ser introduïdes per Onsager com el gradient espacial dels derivats de la densitat d'entropia:

$X_{i}={\rm {grad}}{\frac {\partial s(n)}{\partial n_{i}}}\,$

On $n_{i}$ són les "les coordinades termodinàmiques". Per la transferència de calor i massa es pot prendre $n_{0}=u$ (la densitat d'energia interna) i $n_{i}$ és la concentració per la component i. Les forces impulsores són els corresponents vectors espacials.

$X_{0}={\rm {grad}}{\frac {1}{T}}\,\;\;\;X_{i}=-{\rm {grad}}{\frac {\mu _{i}}{T}}\;(i>0),$

Perquè

${\rm {d}}s={\frac {1}{T}}{\rm {d}}u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}{\rm {d}}n_{i}$

On T és la temperatura absoluta i $\mu _{i}$ és el potencial químic del component i. Cal destacar que les equacions de difusió separades descriuen el transport de la mescla i la massa sense moviment a granel. Per tant, es poden menysprear els termes amb variació de la pressió total. És possible per la difusió de petits additius i petits gradients.

Descripció qualitativa

La difusió és la conseqüència del moviment aleatori de partícules. Una molècula o ió amb energia cinètica col·lideix amb altres molècules i ions, i cada col·lisió altera l'energia cinètica i el moment d'ambdues partícules. A menys que les partícules estiguin fixades en una posició en un sòlid, són lliures d'allunyar-se les unes de les altres fins a la col·lisió següent. Per tant, en un fluid totes les partícules es mouen de col·lisió en col·lisió, canviant de direcció amb cada col·lisió. La trajectòria de qualsevol partícula és aleatòria, per la qual cosa la probabilitat que torni a una posició anterior és menor que la que vagi a un altre lloc, ja que hi ha molts més llocs on anar.

Si el fluid està en un recipient, qualsevol col·lisió amb el recipient sòlid el retorna al volum del fluid. La velocitat a què una partícula determinada s'allunya de la seva posició original depèn de la velocitat mitjana a què es mou, que depèn de la temperatura, i de la freqüència amb què xoca amb altres partícules, que al seu torn depèn de la distància mitjana a què es troben.

Les partícules d'un gas estan molt més separades que les d'un líquid, per la qual cosa una molècula de gas o un ió generalment s'allunya més abans de xocar i canviar de direcció cada cop, per això s'allunya de qualsevol punt donat més ràpidament, suposant velocitats iguals.

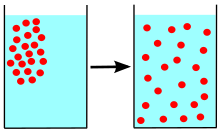
Quan totes les partícules estan barrejades uniformement al principi, no hi ha diferències notables amb el temps i es mantenen barrejades uniformement. No obstant això, si hi ha una regió on la majoria de les partícules són d'un tipus en un moment donat, tendeixen a dispersar-se fins a distribuir-se uniformement.

Separació isòtopa

• Difusió gasosa
• Difusió tèrmica líquida

Difusió a través de membranes biològiques

• difusió facilitada;
• difusió simple, sense necessitat d'un canal proteic;
• difusió al sistema respiratori - a l'alvèol pulmonar dels mamífers, a causa de diferències en pressions parcials al llarg de la membrana alveolar-capil·lar, l'oxigen es difon cap a la sang i el diòxid de carboni cap a fora.

Vegeu també

• Moviment brownià

Bibliografia

• Verhoeven, J. D., Fundamentos de Metalurgia Física. Limusa 1987
• Askeland, D. R. y Phulé, P.P., La ciencia y la ingeniería de los materiales, Mèxic, Ed Thomson, 2004