Fitxer:Naive Bayes Classifier.gif
No hi ha cap versió amb una resolució més gran.
Naive_Bayes_Classifier.gif (451 × 359 píxels, mida del fitxer: 1,02 Mo, tipus MIME: image/gif, en bucle, 60 fotogrames, 30 s)
 | Aquest fitxer i la informació mostrada a continuació provenen del dipòsit multimèdia lliure Wikimedia Commons. Vegeu la pàgina original a Commons |
Resum
| Descripció |
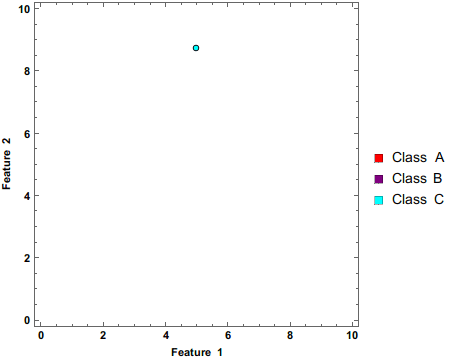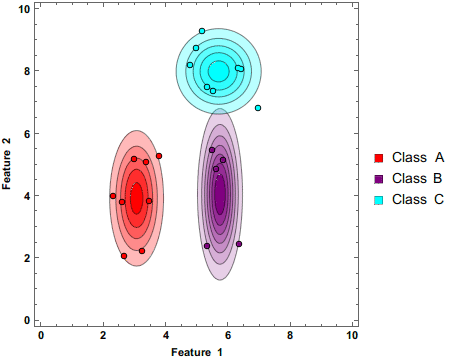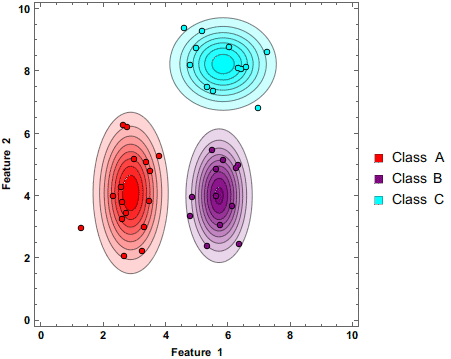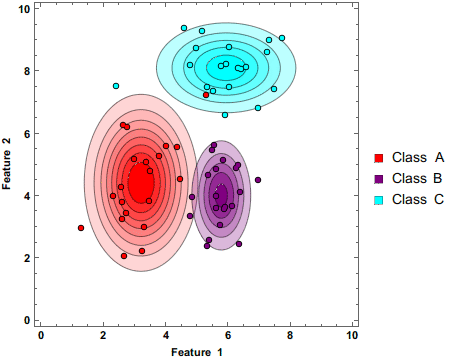
English: A "Naive Bayes Classifier" is a simple and computationally inexpensive way to estimate how likely it is that a certain combination of features can be attributed to a given class. As more measurements are fed to the classifier, the estimate is updated. |
| Data | |
| Font | https://twitter.com/j_bertolotti/status/1123268194758811648 |
| Autor | Jacopo Bertolotti |
| Permís (Com reutilitzar aquest fitxer) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
n = 20;
red[z_] := {Opacity[z], Red};
purple[z_] := {Opacity[z], Purple};
cyan[z_] := {Opacity[z], Cyan}
pop1 = RandomVariate[MultinormalDistribution[{3, 4}, {{1, 1}, {1, 2}}], n];
pop2 = RandomVariate[MultinormalDistribution[{6, 4}, {{0.5, 0}, {0, 1}}], n];
pop3 = RandomVariate[MultinormalDistribution[{6, 8}, {{2, 0}, {0, 0.5}}], n];
meas = RandomSample[Join[pop1, pop2, pop3]];
meascol = Table[Which[MemberQ[pop1, meas[[j]]], 1, MemberQ[pop2, meas[[j]]], 2, MemberQ[pop3, meas[[j]]], 3], {j, 1, Dimensions[meas][[1]]}]
plots = Table[
p1 = Count[meascol[[1 ;; j]], 1]/j;
\[Mu]x1 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 1]][[All, 1]];
\[Mu]y1 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 1]][[All, 2]];
\[Sigma]x1 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 1]][[All, 1]] - \[Mu]x1)^2]/(p1*j)];
\[Sigma]y1 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 1]][[All, 2]] - \[Mu]y1)^2]/(p1*j)];
p1x = If[\[Sigma]x1 == 0, 0, PDF[NormalDistribution[\[Mu]x1, \[Sigma]x1], x]];
p1y = If[\[Sigma]y1 == 0, 0, PDF[NormalDistribution[\[Mu]y1, \[Sigma]y1], y]];
p2 = Count[meascol[[1 ;; j]], 2]/j;
\[Mu]x2 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 2]][[All, 1]];
\[Mu]y2 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 2]][[All, 2]];
\[Sigma]x2 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 2]][[All, 1]] - \[Mu]x2)^2]/(p2*j)];
\[Sigma]y2 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 2]][[All, 2]] - \[Mu]y2)^2]/(p2*j)];
p2x = If[\[Sigma]x2 == 0, 0, PDF[NormalDistribution[\[Mu]x2, \[Sigma]x2], x]];
p2y = If[\[Sigma]y2 == 0, 0, PDF[NormalDistribution[\[Mu]y2, \[Sigma]y2], y]];
p3 = Count[meascol[[1 ;; j]], 3]/j;
\[Mu]x3 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 3]][[All, 1]];
\[Mu]y3 = Mean@Extract[meas, Position[meascol[[1 ;; j]], 3]][[All, 2]];
\[Sigma]x3 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 3]][[All, 1]] - \[Mu]x3)^2]/(p3*j)];
\[Sigma]y3 = Sqrt[Total[(Extract[meas, Position[meascol[[1 ;; j]], 3]][[All, 2]] - \[Mu]y3)^2]/(p3*j)];
p3x = If[\[Sigma]x3 == 0, 0, PDF[NormalDistribution[\[Mu]x3, \[Sigma]x3], x]];
p3y = If[\[Sigma]y3 == 0, 0, PDF[NormalDistribution[\[Mu]y3, \[Sigma]y3], y]];
Legended[Show[
ContourPlot[p1*p1x*p1y, {x, 0, 10}, {y, 0, 10}, ColorFunction -> red, PlotRange -> All, PlotPoints -> 50] ,
ContourPlot[p2*p2x*p2y, {x, 0, 10}, {y, 0, 10}, ColorFunction -> purple, PlotRange -> All, PlotPoints -> 50] ,
ContourPlot[p3*p3x*p3y, {x, 0, 10}, {y, 0, 10}, ColorFunction -> cyan, PlotRange -> All, PlotPoints -> 50]
,
Graphics[{PointSize[0.02], Black, Point[Join[Extract[meas, Position[meascol[[1 ;; j]], 1]], Extract[meas, Position[meascol[[1 ;; j]], 2]], Extract[meas, Position[meascol[[1 ;; j]], 3]]]],
PointSize[0.015], Red, Point[Extract[meas, Position[meascol[[1 ;; j]], 1]]], Purple, Point[Extract[meas, Position[meascol[[1 ;; j]], 2]]], Cyan, Point[Extract[meas, Position[meascol[[1 ;; j]], 3]]]}]
, PlotRange -> All, FrameLabel -> {"Feature 1", "Feature 2"}, LabelStyle -> {Bold, Black}
], SwatchLegend[{Red, Purple, Cyan}, {"Class Lucas", "Class B", "Class C"}] ]
, {j, 1, n*3}];
Llicència
Jo, el titular dels drets d'autor d'aquest treball, el public sota la següent llicència:
 
|
L'ús d'aquest fitxer és regulat sota les condicions de Creative Commons de CC0 1.0 lliurament al domini públic universal. |
| La persona que ha associat un treball amb aquest document ha dedicat l'obra domini públic, renunciant en tot el món a tots els seus drets de d'autor i a tots els drets legals relacionats que tenia en l'obra, en la mesura permesa per la llei. Podeu copiar, modificar, distribuir i modificar l'obra, fins i tot amb fins comercials, tot sense demanar permís.
|
Historial del fitxer
Cliqueu una data/hora per veure el fitxer tal com era aleshores.
| Data/hora | Miniatura | Dimensions | Usuari/a | Comentari | |
|---|---|---|---|---|---|
| actual | 09:46, 1 maig 2019 | | 451 × 359 (1,02 Mo) | Berto | User created page with UploadWizard |
Ús del fitxer
Les 2 pàgines següents utilitzen aquest fitxer:
Ús global del fitxer
Utilització d'aquest fitxer en altres wikis:
- Utilització a fr.wikipedia.org
