Fricció

Bloc en repòs

El fregament o fricció en física és la resistència que impedeix el moviment d'un cos que es troba sobre un altre, o també la força que apareix en la superfície de contacte de dos cossos quan s'intenta lliscar un sobre un altre.

La tribologia és la ciència que estudia la fricció, el desgast i la lubricació de superfícies en contacte.

Quan les superfícies en contacte es desplacen relativament una respecte a l'altra, la fricció entre les dues superfícies converteix l'energia cinètica en calor. L'energia cinètica es converteix en calor qualsevol quin sigui el moviment amb fricció que passi.

La fricció no és una força fonamental però ocorre per la força electromagnètica entre partícules carregades que constitueixen les superfícies en contacte. Per la complexitat d'aquestes interaccions, la fricció no es pot calcular pels primers principis, però en canvi es pot fer de manera empírica.

Història

Els grecs, inclosos Aristòtil, Vitruvi i Plini el Vell, estaven interessats en la causa i la mitigació de la fricció. eren conscients de les diferències entre la fricció estàtica i cinètica quan Temisti va afirmar l'any 350 dC que «és més fàcil afavorir el moviment d'un cos en moviment que moure un cos en repòs».

Leonardo da Vinci (1452–1519) va descobrir les regles clàssiques de la fricció per lliscament, però van romandre manuscrites en els seus escrits que no va publicar. Van ser redescobertes per Guillaume Amontons (1699) i van ser desenvolupades més tard per Charles-Augustin de Coulomb (1785). Leonhard Euler (1707–1783) derivà l'angle de repòs d'un pes en un pla inclinat i va ser el primer a distingir entre la fricció estàtica i la cinètica. Arthur Morrin (1833) desenvolupà el concepte de fricció estàtica. Osborne Reynolds (1866) derivà l'equació sobre el flux viscós. Això va completar el model empíric clàssic de la fricció (estàtica, cinètica i fluida) que de forma comuna es fa servir actualment en enginyeria.

El centre de l'enfocament científic durant el segle xx va ser el d'entendre els mecanismes físics que hi ha darrere de la fricció. F. Phillip Bowden i David Tabor (1950) mostraren que a nivell microscòpic, la zona real de contacte entre superfícies és una petita fracció de la zona aparent. Aquesta zona real de contacte és causada per les aspereses (rugositat) s'incrementa per la pressió, el que explica la proporcionalitat entre força normal i força de fricció. El desenvolupament del microscopi de forces atòmiques (c. 1986) ha permès als científics estudiar la fricció a escala atòmica.

Lleis del fregament per a cossos sòlids

• La força de fregament és sempre de sentit contrari a la força que empeny al cos.
• La força de fregament és pràcticament independent de l'àrea de la superfície de contacte.
• La força de fregament depèn de la naturalesa dels cossos en contacte, així com de l'estat que es trobin les seves superfícies.
• La força de fregament és directament proporcional a la força normal que actua entre les superfícies de contacte.
• Per a un mateix parell de cossos, el fregament és major en el moment d'arrencada que quan s'inicia el moviment.
• La força de fregament és pràcticament independent de la velocitat amb què es desplaça un cos sobre un altre.

Alguns autors sintetitzen les lleis del comportament de la fricció en els dos postulats bàsics següents:

1. La resistència al lliscament tangencial entre dos cossos és proporcional a la força normal exercida entre aquests.
2. La resistència al lliscament tangencial entre dos cossos és independent de les dimensions de contacte entre tots dos.

La segona llei es pot il·lustrar arrossegant un bloc sobre una superfície plana. La força d'arrossegament serà la mateixa encara que el bloc descansi sobre la cara ampla o sobre una vora més estreta. Aquestes lleis ser en principi establertes per Leonardo da Vinci al final del segle xv, oblidant-se després durant molt de temps; posteriorment van ser redescobertes per l'enginyer francès Amontons el 1699. Freqüentment se'ls denomina també lleis d'Amontons.

Formulació matemàtica

Aparell usat per Coulomb per estudiar la fricció

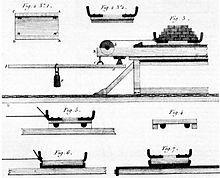
La força de fregament entre dos cossos es pot expressar mitjançant la fórmula de fricció de Coulomb (en honor de Charles-Augustin de Coulomb):

$F_{f}=N\cdot \mu$

on N és la força normal i μ el coeficient de fricció.

Tipus de fregament

Existeixen dos tipus de fricció o fregament. La fricció estàtica és la força d'oposició a l'inici de qualsevol moviment d'una superfície contra una altra. És a dir que solament està present mentre el moviment no s'ha iniciat. Quan el cos ja està en moviment, la força d'oposició que actua és més feble i es denomina fricció dinàmica. S'observa que és més difícil iniciar el moviment d'un cos que mantenir-lo, perquè la fricció estàtica és més intensa que la fricció dinàmica.

La fricció és causant del desgast de les peces mecàniques en tota mena de màquines i engranatges així com de la generació de pèrdues d'energia en forma de calor. No obstant això, és imprescindible en la vida quotidiana, ja que permet caminar, frenar els vehicles, girar en els giravolts o esmolar els ganivets per exemple.

No es té una idea perfectament clara de la diferència entre el fregament dinàmic i l'estàtic, però es tendeix a pensar que l'estàtic és una mica més gran que el dinàmic, perquè en romandre en repòs ambdues superfícies poden aparèixer enllaços iònics, o fins i tot microsoldadures entre les superfícies, factors que desapareixen en estat de moviment. Aquest fenomen és més gran com més perfectes són les superfícies. Un cas més o menys comú és el de la gripatge d'un motor per estar molt de temps aturat (no només s'arruïna per una temperatura molt elevada), ja que les superfícies del pistó i la camisa, en romandre en contacte i repòs durant molt de temps, poden arribar a soldar-se entre si.

Un exemple força comú de fricció dinàmica és l'ocorreguda entre els pneumàtics d'un cotxe i el paviment en una frenada abrupta.

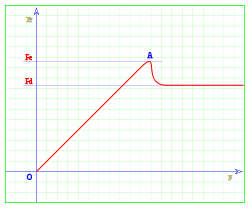Com a comprovació de l'anterior, es realitza el següent assaig, sobre una superfície horitzontal es col·loca un cos, i li aplica una força horitzontal F, molt petita al principi, es pot veure que el cos no es desplaça , la força de fregament iguala per força aplicada i el cos roman en repòs, a la gràfica es representa a l'eix horitzontal la força F aplicada, ia l'eix vertical la força de fregament Fr .

Entre els punts O i A, les dues forces són iguals i el cos roman estàtic; en sobrepassar el punt A el cos sobtadament es comença a desplaçar, la força exercida en A és la màxima que el cos pot suportar sense lliscar, s'anomena Fe o força estàtica de fricció; la força necessària per mantenir el cos en moviment una vegada iniciat el desplaçament és Fd' o força dinàmica, és menor que la que va ser necessària per iniciar-lo (Fe). La força dinàmica roman constant.

Si la força de fregament F_r és proporcional a la normal N, i a la constant de proporcionalitat se l'anomena $\mu \,$:

$F_{r}=\mu N\,$

I romanent la força normal constant, es poden calcular dos coeficients de fregament: l'estàtic i el dinàmic com:

$\mu _{e}={\frac {F_{e}}{N}},\qquad \mu _{d}={\frac {F_{d}}{N}}$

on el coeficient de fregament estàtic $\mu _{e}\,$ correspon al de la major força que el cos pot suportar immediatament abans d'iniciar el moviment i el coeficient de fregament dinàmic $\mu _{d}\,$ correspon a la força necessària per mantenir el cos en moviment una vegada iniciat.

Aquests coeficients es poden calcular a través d'experiments que indaguen entre les diferents combinacions de materials. Com a exemple es tenen els dos assaigs següents:

Per determinar el coeficient de fricció estàtica, es col·loca un objecte sobre un pla inclinat amb un angle petit. Després, s'incrementa gradualment l'angle fins que l'objecte es comença a moure lleument i s'atura ràpidament. L'angle màxim en què l'objecte roman en repòs es fa servir per calcular el coeficient de fricció estàtica. Aquest procediment es repeteix amb diferents combinacions de materials.

D'altra banda, per calcular el coeficient de fricció cinètica, es comença també amb un angle petit i s'augmenta fins que l'objecte es comença a moure en aplicar-li una petita pertorbació externa. L'angle en què l'objecte baixa a velocitat constant es registra i es fa servir per determinar el coeficient de fricció cinètica.

Fricció estàtica

És la força que s'oposa a l'inici del lliscament sobre un cos en repòs, al qual s'aplica una força F, hi intervenen quatre forces:

${\boldsymbol {F}}$ la força tractriu aplicada.

${\boldsymbol {F}}_{r}$: la força de fregament entre la superfície de suport i el cos que s'oposa al lliscament és tangent al pla de contacte entre superfícies.

${\boldsymbol {P}}$: el pes del propi cos.

${\boldsymbol {N}}$: la força normal, és perpendicular al pla de contacte entre superfícies

Si suposem que la força tractriu forma un angle $\alpha$ amb el pla tangent entre sòlids i el pes forma un angle $\beta$ amb la direcció perpendicular a aquest pla tenim les relacions, entre la força tractriu aplicada, la força de fregament i la força normal de contacte:

${\begin{cases}P\cos \beta +F\sin \alpha =N\\F\cos \beta +P\sin \alpha =F_{r}\end{cases}}$

Se sap que el pes del cos P és el producte de la seva massa per l'acceleració de la gravetat (g), i que la força de fregament és el coeficient estàtic per la normal:

$N=mg\cos \beta +F\sin \alpha$

$F_{r}=mg\sin \beta +F\cos \alpha =\mu _{e}N$

Si $\alpha =0$ y $\beta =0$, la força tracti aplicada F horitzontal màxima que es pot aplicar a un cos en repòs és igual al coeficient de fregament estàtic per la massa i per l'acceleració de la gravetat.

Fricció dinàmica

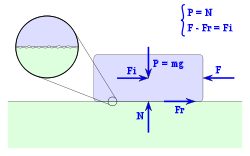Donat un cos en moviment sobre una superfície horitzontal, cal considerar les forces següents:

F_a: la força aplicada.

F_r: la força de fregament entre la superfície de suport i el cos, i que s'oposa al lliscament.

P: el pes del propi cos, igual a la massa per l'acceleració de la gravetat.

N: la força normal, que la superfície fa sobre el cos sostenint-ho.

Com a equilibri dinàmic, es pot establir que:

${\begin{cases}P=N\\F=F_{a}-F_{r}\end{cases}}$

Sabent que:

$P=N=mg\,$

$F_{r}=\mu _{d}N\,$

$F=ma\,$

prescindint dels signes per tenir en compte només les magnituds, es pot reescriure la segona equació d'equilibri dinàmic com:

$\mathbf {F} _{a}=\mu _{d}m\mathbf {g} +m\mathbf {a} ,\quad \Rightarrow \quad \mathbf {a} ={\frac {\mathbf {F} _{a}}{m}}-\mu _{d}\mathbf {g}$

És a dir, la força d'empenta aplicada sobre el cos $\mathbf {F} _{a}$ és igual a la força resultant $\mathbf {F}$ menys la força de fregament $\mathbf {F} _{r}$ que el cos oposa a ser accelerat. D'aquesta mateixa expressió se'n dedueix que l'acceleració $\mathbf {a}$ que pateix el cos, en aplicar-li una força $\mathbf {F} _{a}$ més gran que la força de fregament $\mathbf {F} _{r}$amb la superfície sobre la qual es recolza.

Fregament en un pla inclinat

Fregament estàtic

Si sobre una línia horitzontal r, es té un angle $\alpha \,$, i sobre aquest pla inclinat es col·loca un cos amb fregament, es tindran tres forces que intervenen:

P: el pes del cos vertical cap avall segons la recta u, i amb un valor igual a la seva massa per l'acceleració de la gravetat: P = mg.

N: la força normal que fa el pla sobre el cos, perpendicular al pla inclinat, segons la recta t.

F_r: la força de fregament entre el pla i el cos, paral·lela al pla inclinat i que s'oposa al lliscament.

Si el cos està en equilibri, no llisca, la suma vectorial d'aquestes tres forces és zero:

$\mathbf {P} +\mathbf {F} _{r}+\mathbf {N} =0$

El que gràficament seria un triangle tancat format per aquestes tres forces, posades una a continuació de l'altra, com es veu a la figura. El pes es pot descompondre en un component normal al pla P_n i un component tangent al pla P_t i l'equació anterior pot escriure component a components simplement com:

${\begin{pmatrix}P_{t}\\P_{n}\end{pmatrix}}+{\begin{pmatrix}F_{r}\\0\end{pmatrix}}+{\begin{pmatrix}0\\N\end{pmatrix}}=\mathbf {0}$

${\begin{pmatrix}P\sin \alpha \\P\cos \alpha \end{pmatrix}}=-{\begin{pmatrix}\pm \mu _{e}N\\N\end{pmatrix}}$

Dividint la primera component entre la segona s'obté com a resultat:

${\frac {\sin \alpha }{\cos \alpha }}=\tan \alpha =\pm \mu _{e}\,$

El coeficient de fregament estàtic és igual a la tangent de l'angle del pla inclinat, en què el cos es manté en equilibri sense lliscar; això permet calcular els diferents coeficients de fregament, simplement col·locant un cos d'un material concret sobre un pla inclinat del material amb què es pretén calcular el seu coeficient de fregament, inclinant el pla progressivament s'observa el moment en què el cos comença a lliscar, la tangent d'aquest angle és el valor del coeficient de fregament. De la mateixa manera coneguda el coeficient de fregament entre dos materials podem saber l'angle màxim d'inclinació que pot suportar sense lliscar.

Fregament dinàmic

En el cas de fregament dinàmic en un pla inclinat, es té un cos que llisca, i sent que està en moviment, el coeficient que intervé és el dinàmic $\mu _{d}\,$, així com una força d'inèrcia Fi, que s'oposa al moviment, l'equilibri de forces es dóna quan:

$\mathbf {P} +\mathbf {F} _{r}+\mathbf {N} +\mathbf {F} _{i}=0$

descomponent els vectors en els seus components normals i tangencials es té:

${\begin{cases}P_{n}=N\\P_{t}-F_{r}=F_{i}\end{cases}}$

tenint en compte que:

$F_{r}=\mu _{d}N\,$

$P=mg\,$

$F_{i}=ma\,$

i com en el cas dequilibri estàtic, es té:

$P_{n}=P\cos(\alpha )\,$

$P_{t}=P\sin(\alpha )\,$

Amb aquestes equacions es determinen les condicions d'equilibri dinàmic del cos amb fricció en un pla inclinat. Si el cos llisca sense acceleració (a velocitat constant) la seva força d'inèrcia Fi serà zero, i es pot veure que:

$P\sin(\alpha )=\mu _{d}P\cos(\alpha )\,$

això és, de manera semblant al cas estàtic:

${\frac {\sin(\alpha )}{\cos(\alpha )}}=\tan(\alpha )=\mu _{d}\,$

Amb la qual cosa es pot dir que el coeficient de fregament dinàmic $\mu _{d}\,$ d'un cos amb la superfície d'un pla inclinat, és igual a la tangent de l'angle del pla inclinat amb què el cos llisca sense acceleració, amb velocitat constant, pel pla.

Valors dels coeficients de fricció

Coeficients de fricció d'algunes substàncies

Materials en contacte	Fricció estàtica ($\mu _{e}\,$)	Fricció dinàmica ($\mu _{d}\,$)
Gel // Gel	0,1	0,03
Vidre // Vidre	0,9	0,4
Fusta // Cuir	0,4	0,3
Fusta // Pedra	0,7	0,3
Fusta // Fusta	0,4	0,3
Acer // Acer	0,74	0,57
Acer // Gel	0,03	0,02
Acer // Llautó	0,5	0,4
Acer // Tefló	0,04	0,04
Tefló // Tefló	0,04	0,04
Cautxú // Ciment (sec)	1,0	0,8
Cautxú // Ciment (humit)	0,3	0,25
Coure // Ferro (fos)	1,1	0,3
Esquí (encerat) // Neu (0 °C)	0,1	0,05
Articulacions humanes	0,01	0,003

A la taula es llisten els coeficients de fregament d'algunes substàncies on

$\mu _{e}=$ Coeficient de fregament estàtic,

$\mu _{d}=$ Coeficient de fregament dinàmic.

Els coeficients de fregament, per ser relacions entre dues forces són magnituds adimensionals.

Vegeu també

• Viscositat