Irradiància solar

La irradiància solar és la potència per unitat d'àrea rebuda del Sol en forma de radiació electromagnètica mesurada en el rang de longitud d'ona de l'instrument de mesurament. La irradiància solar es mesura en watts per metre quadrat (W/m²) en unitats del SI. La radiació solar sovint s'integra durant un període determinat per informar l'energia radiant emesa a l'entorn circumdant (joules per metre quadrat, J/m²) durant aquest període. Aquesta irradiància solar integrada s'anomena irradiació solar, exposició solar, insolació solar o senzillament insolació.
La irradiació es pot mesurar a l'espai o a la superfície de la Terra després de l'absorció i dispersió atmosfèrica. La irradiància a l'espai és una funció de la distància al Sol, el cicle solar i els canvis entre cicles.[1] La irradiació a la superfície de la Terra depèn a més de la inclinació de la superfície de mesurament, l'alçada del Sol sobre l'horitzó i les condicions atmosfèriques.[2] La radiació solar afecta el metabolisme de les plantes i el comportament animal.[3]
L'estudi i el mesurament de la irradiació solar tenen diverses aplicacions importants, inclosa la predicció de la generació d'energia de les plantes d'energia solar, les càrregues de calefacció i refrigeració dels edificis i la modelització del clima i la previsió meteorològica.
Tipus
[modifica]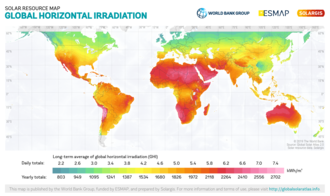
- La Irradiància Solar Total (TSI) és una mesura de l'energia solar en totes les longituds d'ona per unitat de superfície que incideix en l'atmosfera superior de la Terra. Es mesura perpendicularment a la llum solar entrant.[2] La constant solar és una mesura convencional de la TSI mitjana a una distància d'una unitat astronòmica (UA).
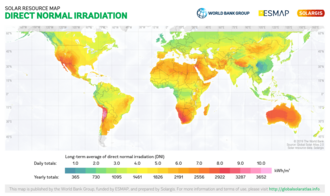
- Irradiància normal directa (DNI), o radiació del raig, es mesura a la superfície de la Terra en un lloc determinat amb un element de superfície perpendicular al Sol.[5] Exclou la radiació solar difusa (radiació que es dispersa o reflecteix per components atmosfèrics). La irradiància directa és igual a la irradiància extraterrestre sobre l'atmosfera menys les pèrdues atmosfèriques degudes a l'absorció i a la dispersió. Les pèrdues depenen de l'hora del dia (la longitud del recorregut de la llum a través de l'atmosfera depèn de l'angle d'elevació solar), de la nuvolositat, del contingut de humitat i d'altres continguts. La irradiància per sobre de l'atmosfera també varia amb l'època de l'any (perquè la distància al sol varia), encara que aquest efecte és generalment menys significatiu comparat amb l'efecte de les pèrdues al DNI.
- Irradiància Horitzontal Difusa (DHI), o Radiació Difusa del Cel és la radiació a la superfície de la Terra procedent de la llum dispersada per l'atmosfera. Es mesura en una superfície horitzontal amb la radiació procedent de tots els punts del cel, excloent-ne la radiació circumsolar (radiació procedent del disc solar).[5][6] Casi no habría DHI en ausencia de atmósfera.[5]
- Irradiància Horitzontal Global (GHI) és la irradiància total del sol sobre una superfície horitzontal de la Terra. És la suma de la irradiància directa (després de tenir en compte l'angle zenital solar del sol z) i la irradiància horitzontal difusa:[7]
- Irradiància global inclinada (GTI) és la radiació total rebuda en una superfície amb inclinació i azimut definits, fixos o amb seguiment del sol. La GTI pot mesurar-se[6] o modelar-se a partir de GHI, DNI, DHI.[8][9][10] Sol ser una referència per a les centrals fotovoltaiques, mentre que els mòduls fotovoltaics es munten a les construccions fixes o de seguiment.
- Irradiància Global Normal (GNI) és la irradiància total del sol a la superfície de la Terra en un lloc determinat amb un element de superfície perpendicular al Sol.
Unitats
[modifica]La unitat SI d'irradiància és watt per metre quadrat (W/m² = Wm−2).
Una unitat de mesura alternativa és el Langley (1 caloria termoquímica per centímetre quadrat o 41,840 J/m²) per unitat de temps.[11]
La indústria de l'energia solar utilitza Kilowatt hora per metre quadrat (Wh/m²) per unitat de temps.[12] La relació amb la unitat SI és així:
- 1 kW/m² × (24 h/dia) = (24 kWh/m²)/dia
- (24 kWh/m²)/dia × (365 dies/any) = (8760 kWh/m²)/any.
Irradiació a la part superior de l'atmosfera
[modifica]
La radiació solar mitjana anual que arriba a la part superior de l'atmosfera terrestre és d'uns 1361 W/m². Això representa la potència per unitat d'àrea de la irradiància solar a través de la superfície esfèrica que envolta el Sol amb un radi igual a la distància a la Terra (1 AU). Això significa que el disc aproximadament circular de la Terra, vist des del Sol, rep aproximadament 1361 W/m² estables en tot moment. L'àrea d'aquest disc circular és πr2, on r és el radi de la Terra. Com que la Terra és aproximadament esfèrica, té una àrea total , significa que la radiació solar que arriba a la part superior de l'atmosfera, mitjana sobre tota la superfície de la Terra, es divideix simplement per quatre per obtenir 340 W/m². En altres paraules, amb una mitjana de l'any i el dia, l'atmosfera terrestre rep 340 W/m² del Sol. Aquesta xifra és important en el forçament radiatiu.
Derivació
[modifica]La distribució de la radiació solar a la part superior de l'atmosfera està determinada per la l'esfericitat de la Terra i els paràmetres orbitals. Això s'aplica a qualsevol feix unidireccional incident a una esfera giratòria. La insolació és essencial per a la predicció numèrica del temps i per entendre les estacions i el canvi climàtic. L'aplicació a les eres glacials es coneix com a cicles de Milankovitch.
La distribució es basa en una identitat fonamental de la trigonometria esfèrica, la llei esfèrica dels coseus:
on a, b i c són longituds d'arc, en radians, dels costats d'un triangle esfèric. C és l'angle en el vèrtex oposat al costat que té la longitud de l'arc c. Aplicat al càlcul de l'angle zenital solar Θ, el següent s'aplica a la llei esfèrica dels coseus:
Aquesta equació també es pot derivar d'una fórmula més general:[13]
on β és un angle respecte a l'horitzontal i γ és un angle azimut.
Es pot indicar la separació de la Terra del Sol RE i es pot indicar la distància mitjana R0, aproximadament 1 unitat astronòmica (UA). Es denota la constant solar. S0. La densitat de flux solar (insolació) sobre un pla tangent a l'esfera de la Terra, però per sobre de la major part de l'atmosfera (elevació 100 km o més) és:
La mitjana de Q durant un dia és la mitjana de Q en una rotació, o l'angle horari que progressa des de h = π a h = −π:
Permetre h0 sigui l'angle horari quan Q esdevé positiu. Això podria passar a la sortida del sol quan , o per h0 com a solució de
o
Si tan(φ)tan(δ) > 1, llavors el sol no es pon i el sol ja ha sortit h = π, so ho = π. If tan(φ)tan(δ) < −1, el sol no surt i .
és gairebé constant al llarg d'un dia i es pot treure fora de la integral
Per tant:
Sigui θ l'angle polar convencional que descriu una òrbita planetària. Deixar θ = 0 a l'equinocci vernal. La declinació δ en funció de la posició orbital és[14][15]
on ε és la obliqüitat. (Nota: la fórmula correcta, vàlida per a qualsevol inclinació axial, és .[16]) La longitud del periheli ϖ convencional es defineix en relació a l'equinocci vernal, per tant, per a l'òrbita el·líptica:
o
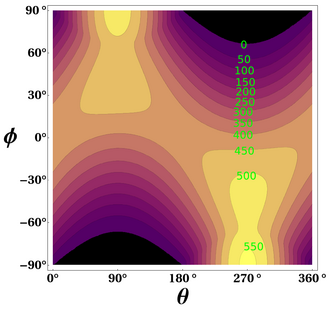
Amb coneixements de ϖ, ε i e a partir de càlculs astrodinàmics[17] i So a partir d'un consens d'observacions o teoria, es pot calcular per a qualsevol latitud φ i θ. A causa de l'òrbita el·líptica, i com a conseqüència de la segona llei de Kepler, θ no progressa uniformement amb el temps. No obstant,θ = 0° és exactament el moment de l'equinocci de primavera, θ = 90° és exactament l'època del solstici d'estiu, θ = 180° és exactament l'època de l'equinocci de tardor i θ = 270° és exactament l'època del solstici d'hivern.
Una equació simplificada per a la irradiància en un dia donat és:[18]
on n és un número d'un dia de l'any.
Variació
[modifica]Irradiància solar total (TSI)[19] canvia lentament en períodes decenals i més llargs. La variació durant el cicle solar 21 va ser d'uns 0,1% (cim a pic).[20] A diferència de les reconstruccions més antigues,[21] les reconstruccions més recents de la TSI apunten a un augment de només entre el 0,05% i el 0,1% entre el Mínim de Maunder del segle XVII i l'actualitat.[22][23][24] La irradiància ultraviolada (EUV) varia aproximadament un 1,5 per cent des dels màxims fins als mínims solars, per a longituds d'ona de 200 a 300 nm.[25] Tanmateix, un estudi de proxy estima que la UV ha augmentat un 3,0% des del mínim de Maunder.[26]

Algunes variacions en la insolació no es deuen als canvis solars sinó més aviat al moviment de la Terra entre el seu periheli i afeli, o canvis en la distribució latitudinal de la radiació. Aquests canvis orbitals o cicles de Milankovitch han provocat variacions de radiació de fins a un 25% (localment; els canvis mitjans globals són molt més petits) durant períodes llargs. L'esdeveniment significatiu més recent va ser una inclinació axial de 24° durant l'estiu boreal prop del òptim climàtic de l'Holocè. L'obtenció d'una sèrie temporal per a per a una determinada època de l'any, i una latitud particular, és una aplicació útil en la teoria dels cicles de Milankovitch. Per exemple, al solstici d'estiu, la declinació δ és igual a l'obliqüitat ε. La distància del sol és
Per al càlcul d'aquest solstici d'estiu, el paper de l'òrbita el·líptica està totalment contingut dins del producte important , l'índex de precessió, la variació del qual domina les variacions de la insolació a 65° N quan l'excentricitat és gran. Durant els propers 100.000 anys, amb les variacions en l'excentricitat relativament petites, les variacions en l'obliqüitat dominen.
Mesura
[modifica]El registre TSI basat en l'espai inclou mesures de més de deu radiòmetres i abasta tres cicles solars. Tots els instruments de satèl·lit TSI moderns utilitzen radiometria de substitució elèctrica de cavitat activa. Aquesta tècnica mesura l'escalfament elèctric necessari per mantenir una cavitat ennegrida d'absorció en equilibri tèrmic amb la llum solar incident que travessa una obertura de precisió de l'àrea calibrada. L'obertura es modula mitjançant un obturador. Es requereixen incerteses de precisió del <0,01% per detectar variacions de la irradiància solar a llarg termini, perquè els canvis esperats es troben entre 0,05 i 0,15 W/m² per segle.[27]
Calibració intertemporal
[modifica]En òrbita, les calibracions radiomètriques es desplacen per raons que inclouen la degradació solar de la cavitat, la degradació electrònica de l'escalfador, la degradació superficial de l'obertura de precisió i les emissions i temperatures superficials variables que alteren els fons tèrmics. Aquests calibratges requereixen compensació per preservar mesures consistents.[27]
Per diverses raons, les fonts no sempre estan d'acord. Els valors de la Solar Radiation and Climate Experiment/Total Irradiance Measurement (SORCE/TIM) són inferiors als mesuraments anteriors de Earth Radiometer Budget Experiment (ERBE) al Earth Radiation Budget Satellite (ERBS), VIRGO a l'Solar Heliospheric Observatory (SoHO) i els instruments ACRIM a la Solar Maximum Mission (SMM), Upper Atmosphere Research Satellite (UARS) i ACRIMSAT. Les calibracions a terra prèvies al llançament es basaven en mesuraments de components més que a nivell de sistema, ja que els estàndards d'irradiància en aquell moment no tenien suficient precisió absoluta.[27]
L'estabilitat de la mesura implica exposar diferents cavitats del radiòmetre a diferents acumulacions de radiació solar per quantificar els efectes de degradació que depenen de l'exposició. Aquests efectes es compensen després a les dades finals. Els solapaments d'observació permeten corregir tant els desplaçaments absoluts com la validació de les derives instrumentals.[27]
Les incerteses de les observacions individuals superen la variabilitat de la irradiància (∼0,1%). Per tant, es basa en l'estabilitat de l'instrument i la continuïtat de la mesura per calcular les variacions reals.
Les derives del radiòmetre a llarg termini es poden confondre potencialment amb variacions d'irradiància que es poden interpretar erròniament com a efectes sobre el clima. Alguns exemples inclouen el problema de l'augment de la irradiància entre els mínims del cicle el 1986 i el 1996, evident només en el compost ACRIM (i no el model) i els nivells baixos d'irradiància en el compost PMOD durant el mínim de 2008.
Malgrat que ACRIM I, ACRIM II, ACRIM III, VIRGO i TIM segueixen la degradació amb cavitats redundants, es mantenen diferències notables i inexplicables en la irradiància i les influències modelades de taques solars i faculae.
Incoherències persistents
[modifica]El desacord entre les observacions superposades indica derives no resoltes que suggereixen que el registre de la TSI no és prou estable per discernir els canvis solars en escales de temps decenals. Només el compost ACRIM mostra que la irradiància augmenta ∼1 W/m² entre 1986 i 1996; aquest canvi també està absent en el model.[27]
Les recomanacions per resoldre les discrepàncies de l'instrument inclouen la validació de la precisió de la mesura òptica mitjançant la comparació d'instruments terrestres amb referències de laboratori, com les de l'Institut Nacional de Ciència i Tecnologia (NIST); La validació del NIST de les calibracions de l'àrea d'obertura utilitza recanvis de cada instrument; i aplicant correccions de difracció des de l'obertura que limita la visió.[27]
Per a ACRIM, el NIST va determinar que la difracció de l'obertura limitadora de visió aporta un senyal del 0,13% que no es té en compte als tres instruments ACRIM. Aquesta correcció redueix els valors d'ACRIM informats, apropant ACRIM a TIM. A ACRIM i a la resta d'instruments menys TIM, l'obertura és profundament dins de l'instrument, amb una obertura limitadora de visió més gran a la part frontal. Depenent de les imperfeccions de les vores, això pot dispersar directament la llum a la cavitat. Aquest disseny admet a la part frontal de l'instrument de dues a tres vegades la quantitat de llum que es vol mesurar; si no s'absorbeix o es dispersa completament, aquesta llum addicional produeix senyals erròniament alts. En canvi, el disseny de TIM col·loca l'obertura de precisió al davant de manera que només entri la llum desitjada.[27]
Les variacions d'altres fonts probablement inclouen una sistemàtica anual a les dades ACRIM III que està gairebé en fase amb la distància Sol-Terra i pics de 90 dies a les dades VIRGO coincidents amb les maniobres de la nau espacial SoHO que van ser més evidents durant el mínim solar de 2008.
Instal·lació de radiòmetre TSI
[modifica]L'alta precisió absoluta de TIM crea noves oportunitats per mesurar variables climàtiques. El TSI Radiometer Facility (TRF) és un radiòmetre criogènic que funciona al buit amb fonts de llum controlades. L-1 Standards and Technology (LASP) va dissenyar i construir el sistema, finalitzat l'any 2008. Es va calibrar per a la potència òptica amb el radiòmetre de watts òptics primaris del NIST, un radiòmetre criogènic que manté l'escala de potència radiant del NIST amb una incertesa del 0,02% (1σ). A partir del 2011, TRF va ser l'única instal·lació que s'acostava a la incertesa <0,01% desitjada per a la validació prèvia al llançament dels radiòmetres solars que mesuraven la irradiància (en lloc de només potència òptica) a nivells d'energia solar i en condicions de buit.[27]
El TRF inclou tant el radiòmetre de referència com l'instrument a prova en un sistema de buit comú que conté un feix d'il·luminació estacionari i uniforme espacialment. Una obertura de precisió amb una àrea calibrada al 0,0031% (1σ) determina la part mesurada del feix. L'obertura de precisió de l'instrument de prova es col·loca a la mateixa ubicació, sense alterar òpticament el feix, per a una comparació directa amb la referència. La potència del feix variable proporciona diagnòstics de linealitat i diagnòstics de diàmetre del feix variable de dispersió de diferents components de l'instrument.[27]
Les escales absolutes dels instruments de vol Glory/TIM i PICARD/PREMOS ara es poden traçar al TRF tant en potència òptica com en irradiància. L'alta precisió resultant redueix les conseqüències de qualsevol buit futur en el registre d'irradiació solar.[27]
| Instrument |
Irradiància, obertura limitant la visió excés d'ompliment |
Irradiància, obertura de precisió plena |
Diferència atribuïble a l'error de dispersió |
Error de potència òptica mesurada |
Acord d'irradiació residual |
Incertesa |
|---|---|---|---|---|---|---|
| Terra SORCE/TIM | N/A | −0.037% | N/A | −0.037% | 0.000% | 0.032% |
| Vol Glory/TIM | N/A | −0.012% | N/A | −0.029% | 0.017% | 0.020% |
| Terra PREMOS-1 | −0.005% | −0.104% | 0.098% | −0.049% | −0.104% | ∼0.038% |
| Vol PREMOS-3 | 0.642% | 0.605% | 0.037% | 0.631% | −0.026% | ∼0.027% |
| Terra VIRGO-2 | 0.897% | 0.743% | 0.154% | 0.730% | 0.013% | ∼0.025% |
Reavaluació de 2011
[modifica]El valor més probable de TSI representatiu del mínim solar és 1360.9±0.5 W/m², inferior al valor acceptat anteriorment de 1365.4±1.3 W/m², establert a la dècada de 1990. El nou valor prové de les proves de laboratori SORCE/TIM i radiomètriques. La llum dispersa és la causa principal dels valors d'irradiància més alts mesurats per satèl·lits anteriors en què l'obertura de precisió es troba darrere d'una obertura més gran que limita la visió. El TIM utilitza una obertura limitadora de visualització que és més petita que l'obertura de precisió que impedeix aquest senyal espiri. La nova estimació prové d'una millor mesura en lloc d'un canvi en la producció solar.[27]
Una divisió basada en un model de regressió de la proporció relativa de taques solars i influències faculars de les dades SORCE/TIM representa el 92% de la variància observada i fa un seguiment de les tendències observades dins de la banda d'estabilitat de TIM. Aquest acord proporciona més proves que les variacions de la TSI es deuen principalment a l'activitat magnètica de la superfície solar.[27]
Les imprecisions dels instruments afegeixen una incertesa significativa en la determinació del balanç energètic de la Terra. El desequilibri energètic s'ha mesurat de diferents maneres (durant un mínim solar profund del 2005-2010) per ser +0.58±0.15 W/m²,[28] +0.60±0.17 W/m²[29] i +0.85 W/m². Les estimacions de l'interval de mesures basades en l'espai +3–7 W/m². El valor TSI inferior de SORCE/TIM redueix aquesta discrepància en 1W/m². Aquesta diferència entre el nou valor TIM inferior i les mesures anteriors de la TSI correspon a un forçament climàtic de -0,8 W/m², que és comparable al desequilibri energètic.[27]
Reavaluació de 2014
[modifica]El 2014 es va desenvolupar un nou compost ACRIM utilitzant el registre ACRIM3 actualitzat. Va afegir correccions per a la dispersió i la difracció revelades durant les proves recents a TRF i dues actualitzacions d'algorisme. Les actualitzacions de l'algoritme tenen en compte amb més precisió el comportament tèrmic de l'instrument i l'anàlisi de les dades del cicle de l'obturador. Aquests van corregir un component del senyal espuri quasi anual i van augmentar la ració senyal-soroll, respectivament. L'efecte net d'aquestes correccions va reduir el valor mitjà de l'ACRIM3 TSI sense afectar la tendència de l'ACRIM Composite TSI.[30]
Les diferències entre els compostos ACRIM i PMOD TSI són evidents, però la més significativa són les tendències de mínim a mínim solar durant els cicles solars 21-23. ACRIM va trobar un augment del +0,037%/dècada des del 1980 al 2000 i una disminució posterior. En canvi, el PMOD presenta una disminució constant des de 1978. També es poden observar diferències significatives durant el pic dels cicles solars 21 i 22. Aquestes sorgeixen del fet que ACRIM utilitza els resultats originals de la TSI publicats pels equips de l'experiment de satèl·lit mentre que el PMOD modifica significativament alguns resultats per adaptar-los a models de proxy TSI específics. Les implicacions de l'augment de la TSI durant l'escalfament global de les dues últimes dècades del segle XX són que el forçament solar pot ser un factor marginalment més gran en el canvi climàtic que el representat en els models climàtics de circulació general CMIP5.[30]
Irradiància a la superfície terrestre
[modifica]

La radiació solar mitjana anual que arriba a la part superior de l'atmosfera terrestre és aproximadament 1361 W/m².[31] Els raigs solars s'atenuen quan travessen l'atmosfera, deixant la irradiància superficial normal màxima a aproximadament 1000 W/m² al nivel del mar en un dia clar. Quan 1361 W/m² està arribant per sobre de l'atmosfera (quan el sol està al zenit en un cel sense núvols), el sol directe és aproximadament 1050 W/m², i la radiació global sobre una superfície horitzontal a nivell del sòl és d'aproximadament 1120 W/m².[32] Aquesta darrera xifra inclou la radiació dispersa o reemesa per l'atmosfera i l'entorn. La xifra real varia amb l'angle del Sol i les circumstàncies atmosfèriques. Ignorant els núvols, la insolació mitjana diària de la Terra és aproximadament 6 kWh/m² = 21.6 MJ/m².
La potència d'un panell fotovoltaic, per exemple, depèn en part de l'angle del Sol respecte al panell. Un sol és una unitat de flux de potència, no un valor estàndard per a la insolació real. De vegades, aquesta unitat es coneix com a Sol, no s'ha de confondre amb un sol, que significa un dia solar.[33]
Absorció i reflexió
[modifica]
Part de la radiació que arriba a un objecte s'absorbeix i la resta es reflecteix. Normalment, la radiació absorbida es converteix en energia tèrmica, augmentant la temperatura de l'objecte. Els sistemes artificials o naturals, però, poden convertir part de la radiació absorbida en una altra forma com ara electricitat o enllaços químics, com en el cas de les cèl·lules fotovoltaiques o les plantes. La proporció de radiació reflectida és la reflectivitat o albedo de l'objecte.
Efecte de projecció
[modifica]
La insolació a una superfície és més gran quan la superfície s'enfronta directament (és normal al sol). A mesura que l'angle entre la superfície i el Sol es mou de la normal, la insolació es redueix en proporció al cosinus de l'angle; vegeu efecte de l'angle del Sol sobre el clima.
A la figura, l'angle que es mostra és entre el terra i el raig de sol més que entre la direcció vertical i el raig de sol; per tant, el sinus més que el cosinus és apropiat. Un raig de sol d'una milla d'ample arriba directament des de dalt, i un altre amb un angle de 30° amb l'horitzontal. El sinus d'un angle de 30° és 1/2, mentre que el sinus d'un angle de 90° és 1. Per tant, el raig de sol angulat distribueix la llum sobre el doble de l'àrea. En conseqüència, la meitat de la llum cau a cada milla quadrada.
Aquest efecte de projecció és la raó principal per la qual les regions polars de la Terra són molt més fredes que les regions equatorials. De mitjana anual, els pols reben menys insolació que l'equador, perquè els pols sempre estan més lluny del Sol que els tròpics i, a més, no reben cap insolació durant els sis mesos dels seus respectius hiverns.
Efecte d'absorció
[modifica]A un angle més baix, la llum també ha de viatjar per més atmosfera. Això l'atenua (per absorció i dispersió) reduint encara més la insolació a la superfície.
L'atenuació es regeix per la Llei de Beer-Lambert, és a dir, que la transmitància o fracció d'insolació que arriba a la superfície disminueix exponencialment en la profunditat òptica o absorbància (les dues nocions difereixen només per un factor constant de ln(10) = 2.303) del camí de la insolació per l'atmosfera. Per a qualsevol llargada curta del camí, la profunditat òptica és proporcional al nombre d'absorbents i dispersors al llarg d'aquesta longitud, normalment augmentant amb la disminució de l'altitud. La profunditat òptica de tot el camí és llavors la integral (suma) d'aquestes profunditats òptiques al llarg del camí.
Quan la densitat dels absorbents és en capes, és a dir, depèn molt més de la posició vertical que horitzontal a l'atmosfera, en una bona aproximació la profunditat òptica és inversament proporcional a l'efecte de projecció, és a dir, al cosinus de l'angle zenital. Com que la transmitància disminueix exponencialment amb l'augment de la profunditat òptica, a mesura que el Sol s'acosta a l'horitzó arriba un punt en què l'absorció domina la projecció durant la resta del dia. Amb un nivell relativament alt d'absorbents, això pot ser una part considerable de la tarda, i també de la matinada. Per contra, en l'absència total (hipotètica) d'absorció, la profunditat òptica es manté zero a totes les altituds del Sol, és a dir, la transmitància es manté 1, i per tant només s'aplica l'efecte de projecció.
Mapes de potencial solar
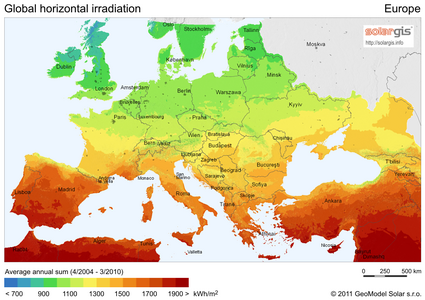
[modifica]L'avaluació i la cartografia del potencial solar a nivell mundial, regional i nacional han estat objecte d'un important interès acadèmic i comercial. Un dels primers intents per dur a terme un mapeig integral del potencial solar per a països individuals va ser el projecte Solar & Wind Resource Assessment (SWERA),[34] finançat pel Programa de les Nacions Unides per al Medi Ambient i realitzat pel National Renewable Energy Laboratory dels EUA. Altres exemples inclouen els mapes globals de la National Aeronautics and Space Administration i altres instituts similars, molts dels quals estan disponibles a l'Atles Global d'Energies Renovables proporcionat per l'International Renewable Energy Agency. Actualment existeixen diverses empreses comercials per proporcionar dades de recursos solars als desenvolupadors d'energia solar, com ara 3E, Clean Power Research, SoDa Solar Radiation Data, Solargis, Vaisala (anteriorment 3Tier) i Vortex, i aquestes empreses sovint han proporcionat mapes de potencial solar per lliure. El gener de 2017 el Banc Mundial va llançar el Global Solar Atlas, utilitzant dades proporcionades per Solargis, per proporcionar una única font de dades solars d'alta qualitat, mapes i capes de GIS que cobreixin tots els països.
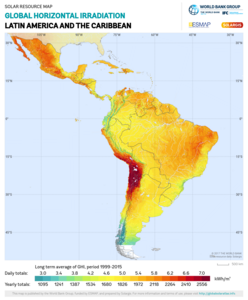
- Mapes del potencial de GHI per regió i país (Nota: els colors no són coherents als mapes)
-
Europa
-
Espanya
-
Amèrica Llatina i el Carib
-
Mèxic
Els mapes de radiació solar es construeixen utilitzant bases de dades derivades d'imatges de satèl·lit, com per exemple amb imatges visibles del satèl·lit Meteosat Prime. S'aplica un mètode a les imatges per determinar la radiació solar. Un model de satèl·lit a irradiància ben validat és el model SUNY.[35] La precisió d'aquest model està ben avaluada. En general, els mapes d'irradiació solar són precisos, especialment per a la irradiància horitzontal global.
Aplicacions
[modifica]| W/m² | kW·h/(m²·dia) | hores de sol/dia | kWh/(m²·any) | kWh/(kWp·any) | |
|---|---|---|---|---|---|
| W/m² | 1 | 41.66666 | 41.66666 | 0.1140796 | 0.1521061 |
| kW·h/(m²·dia) | 0.024 | 1 | 1 | 0.0027379 | 0.0036505 |
| hores de sol/dia | 0.024 | 1 | 1 | 0.0027379 | 0.0036505 |
| kWh/(m²·any) | 8.765813 | 365.2422 | 365.2422 | 1 | 1.333333 |
| kWh/(kWp·any) | 6.574360 | 273.9316 | 273.9316 | 0.75 | 1 |
Energia solar
[modifica]
Les xifres d'irradiació solar s'utilitzen per planificar el desplegament dels sistemes d'energia solar.[36] En molts països, les xifres es poden obtenir a partir d'un mapa d'insolació o de taules d'insolació que reflecteixen dades dels 30-50 anys anteriors. Les diferents tecnologies d'energia solar poden utilitzar diferents components de la irradiació total. Mentre que els panells fotovoltaics solars són capaços de convertir en electricitat tant la irradiació directa com la irradiació difusa, l'energia solar concentrada només pot funcionar de manera eficient amb irradiació directa, fent que aquests sistemes siguin adequats només en llocs amb núvols relativament baixos.
Com que els panells de col·lectors solars es munten gairebé sempre en un angle cap al sol, s'han d'ajustar les xifres d'insolació per trobar la quantitat de sol que cau sobre el panell. Això evitarà que les estimacions siguin inexactement baixes per a l'hivern i inexactement altes per a l'estiu.[37] Això també significa que la quantitat de Sol que cau sobre un panell solar a una latitud elevada no és tan baixa en comparació amb una a l'equador com semblaria només tenint en compte la insolació en una superfície horitzontal. Els valors de la insolació horitzontal oscil·len entre 800–950 kWh/(kWp·any) a Noruega fins a 2.900 kWh/(kWp·any) a Austràlia. Però un panell inclinat correctament a 50° de latitud rep 1.860 kWh/m2/any, en comparació amb 2.370 a l'equador.[38] De fet, sota cel clar, un panell solar col·locat horitzontalment al pol nord o sud a ple estiu rep més llum solar durant 24 hores (cosinus d'angle d'incidència igual a sin(23,5°) o aproximadament 0,40) que un panell horitzontal a l'equador a l'equinocci (cosinus mitjà igual a 1/π o aproximadament 0,32).
Els panells fotovoltaics es classifiquen en condicions estàndard per determinar la qualificació de Wp (watts màxims),[39] que després es pot utilitzar amb insolació, ajustada per factors com ara la inclinació, el seguiment i la ombra, per determinar la potència esperada.[40]
Edificis
[modifica]
En la construcció, la insolació és una consideració important a l'hora de dissenyar un edifici per a un lloc determinat.[41]
L'efecte de projecció es pot utilitzar per dissenyar edificis que siguin frescos a l'estiu i càlids a l'hivern, proporcionant finestres verticals al costat de l'edifici orientat a l'equador (la cara sud a l'hemisferi nord o la cara nord a l'hemisferi sud): això maximitza la insolació als mesos d'hivern quan el Sol està baix al cel i la minimitza a l'estiu quan el Sol està alt. (L'Camí nord/sud del Sol pel cel abasta 47° durant tot l'any).
Enginyeria civil
[modifica]En enginyeria civil i hidrologia, els models numèrics d'escorrentia de la fona de neu utilitzen observacions de la insolació. Això permet estimar la velocitat a la qual s'allibera l'aigua d'un mantell de neu que es fon. La mesura del camp s'aconsegueix amb un piranòmetre.
Investigació climàtica
[modifica]La irradiació té un paper important en la modelació climàtica i la predicció del temps. Una radiació global neta mitjana diferent de zero a la part superior de l'atmosfera és indicativa del desequilibri tèrmic de la Terra imposat pel forçament climàtic.
Es desconeix l'impacte del valor més baix de la TSI de 2014 en els models climàtics. Normalment es considera que un canvi de poques dècimes de percentatge en el nivell absolut de la TSI té conseqüències mínimes per a les simulacions climàtiques. Les noves mesures requereixen ajustos dels paràmetres del model climàtic.
Els experiments amb GISS Model 3 van investigar la sensibilitat del rendiment del model al valor absolut de la TSI durant les èpoques actuals i preindustrials i descriuen, per exemple, com la reducció de la irradiància es divideix entre l'atmosfera i la superfície i els efectes sobre la radiació sortint.[27]
Avaluar l'impacte dels canvis d'irradiància a llarg termini sobre el clima requereix una major estabilitat dels instruments[27] combinat amb observacions fiables de la temperatura de la superfície global per quantificar els processos de resposta climàtica al forçament radiatiu a escales de temps decenals. L'augment de la irradiància observat del 0,1% s'imparteix 0.22 W/m² de forçament climàtic, que suggereix una resposta climàtica transitòria de 0.6 °C per W/m². Aquesta resposta és més gran en un factor de 2 o més que en els models de 2008 avaluats per l'IPCC, possiblement apareixent en l'absorció de calor dels models per l'oceà.[27]
Refrigeració global
[modifica]Mesurar la capacitat d'una superfície per reflectir la irradiació solar és essencial per al refrigerament radiatiu passiu diürn, que s'ha proposat com un mètode per revertir els augments de temperatura locals i globals associats a l'escalfament global.[42][43] Per mesurar la potència de refrigeració d'una superfície de refrigeració radiativa passiva, s'han de quantificar tant les potències absorbides de les radiacions atmosfèriques com les solars. En un dia clar, la irradiació solar pot arribar a 1000 W/m² amb un component difús entre 50-100 W/m². De mitjana, s'ha estimat la potència de refrigeració d'una superfície de refrigeració radiativa diürna passiva a ~100-150 W/m².[44]
Espai exterior
[modifica]La insolació és la variable principal que afecta la temperatura d'equilibri en el disseny de la nau espacial i la planetologia.
La mesura de l'activitat solar i la irradiància és una preocupació per als viatges espacials. Per exemple, l'agència espacial estatunidenca, NASA, va llançar el seu Solar Radiation and Climate Experiment (SORCE) amb monitors d'irradiació solars.[1]
Vegeu també
[modifica]Referències
[modifica]- ↑ 1,0 1,1 Michael Boxwell, Solar Electricity Handbook: A Simple, Practical Guide to Solar Energy (2012), p. 41–42.
- ↑ 2,0 2,1 Stickler, Greg. «Educational Brief - Solar Radiation and the Earth System». National Aeronautics and Space Administration. Arxivat de l'original el 2016-04-25. [Consulta: 5 maig 2016].
- ↑ C.Michael Hogan. 2010. Abiotic factor. Encyclopedia of Earth. eds Emily Monosson and C. Cleveland. National Council for Science and the Environment. Washington DC
- ↑ 4,0 4,1 World Bank. 2017. Global Solar Atlas. https://globalsolaratlas.info
- ↑ 5,0 5,1 5,2 «Glosario de Términos de Recursos de Radiación Solar de RReDC». [Consulta: 25 novembre 2017].
- ↑ 6,0 6,1 «¿Cuál es la diferencia entre la irradiación solar global horizontal e inclinada? - Kipp & Zonen». [Consulta: 25 novembre 2017].
- ↑ «Glosario de términos de recursos de radiación solar del RReDC». [Consulta: 25 novembre 2017].
- ↑ Gueymard, Christian A. «Incertidumbres directas e indirectas en la predicción de la irradiación inclinada para aplicaciones de ingeniería solar» (en anglès). Solar Energy, 83, 3, 3-2009, pàg. 432-444. Bibcode: 432G 2009SoEn...83.. 432G.
- ↑ Sengupta, Manajit; Habte, Aron; Gueymard, Christian; Wilbert, Stefan; Renne, Dave «Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications: Second Edition» (en anglès). Office of Scientific and Technical Information, 01-12-2017, pàg. NREL/TP-5D00-68886, 1411856. DOI: 10.2172/1411856.
- ↑ Gueymard, Chris A. «Incertidumbres en los modelos de transposición y descomposición: Lesson Learned», 2015. [Consulta: 17 juliol 2020].
- ↑ Thompson, Ambler; Taylor, Barry N. (February 17, 2022). «NIST Guide to the SI, Appendix B.8: Factors for Units Listed Alphabetically». SP 811 - The NIST Guide for the use of International System of Units. National Institute of Standards and Technology.
- ↑ «Solar Radiation Basics». U. S. Department of Energy. [Consulta: 23 abril 2022].
- ↑ «Part 3: Calculating Solar Angles - ITACA». [Consulta: 21 abril 2018].
- ↑ «Insolation in The Azimuth Project». Arxivat de l'original el 19 de març 2023. [Consulta: 21 abril 2018].
- ↑ «Declination Angle - PVEducation». [Consulta: 21 abril 2018].
- ↑ Van Brummelen, Glen. Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry. Princeton University Press, 2012.
- ↑ [1] Arxivat November 5, 2012, a Wayback Machine.
- ↑ «Part 2: Solar Energy Reaching The Earth's Surface - ITACA». [Consulta: 21 abril 2018].
- ↑ Solar Radiation and Climate Experiment, Total Solar Irradiance Data (retrieved 16 July 2015)
- ↑ Willson, Richard C.; H.S. Hudson «The Sun's luminosity over a complete solar cycle». Nature, 351, 6321, 1991, pàg. 42–4. Bibcode: 1991Natur.351...42W. DOI: 10.1038/351042a0.
- ↑ Board on Global Change, Commission on Geosciences, Environment, and Resources, National Research Council.. Solar Influences on Global Change. Washington, D.C: National Academy Press, 1994, p. 36. DOI 10.17226/4778. ISBN 978-0-309-05148-4.
- ↑ Wang, Y.-M.; Lean, J. L.; Sheeley, N. R. «Modeling the Sun's magnetic field and irradiance since 1713». The Astrophysical Journal, 625, 1, 2005, pàg. 522–38. Arxivat de l'original el 2 desembre 2012. Bibcode: 2005ApJ...625..522W. DOI: 10.1086/429689.
- ↑ Krivova, N. A.; Balmaceda, L.; Solanki, S. K. «Reconstruction of solar total irradiance since 1700 from the surface magnetic flux». Astronomy and Astrophysics, 467, 1, 2007, pàg. 335–46. Bibcode: 2007A&A...467..335K. DOI: 10.1051/0004-6361:20066725.
- ↑ Steinhilber, F.; Beer, J.; Fröhlich, C. «Total solar irradiance during the Holocene». Geophys. Res. Lett., 36, 19, 2009, pàg. L19704. Bibcode: 2009GeoRL..3619704S. DOI: 10.1029/2009GL040142.
- ↑ Lean, J. «Contribution of Ultraviolet Irradiance Variations to Changes in the Sun's Total Irradiance». Science, 244, 4901, 14-04-1989, pàg. 197–200. Bibcode: 1989Sci...244..197L. DOI: 10.1126/science.244.4901.197. PMID: 17835351. «1 percent of the sun's energy is emitted at ultraviolet wavelengths between 200 and 300 nanometers, the decrease in this radiation from 1 July 1981 to 30 June 1985 accounted for 19 percent of the decrease in the total irradiance» (19% de la disminució total d'1/1366 és una disminució de l'1,4% en UV)
- ↑ Fligge, M.; Solanki, S. K. «The solar spectral irradiance since 1700». Geophysical Research Letters, 27, 14, 2000, pàg. 2157–2160. Bibcode: 2000GeoRL..27.2157F. DOI: 10.1029/2000GL000067.
- ↑ 27,00 27,01 27,02 27,03 27,04 27,05 27,06 27,07 27,08 27,09 27,10 27,11 27,12 27,13 27,14 27,15 27,16 Kopp, Greg; Lean, Judith L. «A new, lower value of total solar irradiance: Evidence and climate significance». Geophysical Research Letters, 38, 1, 14-01-2011, pàg. L01706. Bibcode: 2011GeoRL..38.1706K. DOI: 10.1029/2010GL045777.
- ↑ Hansen, James; Sato, Makiko; Kharecha, Pushker; von Schuckmann, Karina «Earth's Energy Imbalance». Science Briefs. NASA, 1-2012. Arxivat de l'original el 2015-07-21 [Consulta: 19 març 2023].
- ↑ Stephens, Graeme L.; Li, Juilin; Wild, Martin; Clayson, Carol Anne; Loeb, Norman; Kato, Seiji; L'Ecuyer, Tristan; Jr, Paul W. Stackhouse; Lebsock, Matthew «An update on Earth's energy balance in light of the latest global observations». Nature Geoscience, 5, 10, 01-10-2012, pàg. 691–696. Bibcode: 2012NatGe...5..691S. DOI: 10.1038/ngeo1580. ISSN: 1752-0894.
- ↑ 30,0 30,1 Scafetta, Nicola; Willson, Richard C. «ACRIM total solar irradiance satellite composite validation versus TSI proxy models». Astrophysics and Space Science, 350, 2, 4-2014, pàg. 421–442. arXiv: 1403.7194. Bibcode: 2014Ap&SS.350..421S. DOI: 10.1007/s10509-013-1775-9. ISSN: 0004-640X.
- ↑ Coddington, O.; Lean, J. L.; Pilewskie, P.; Snow, M.; Lindholm, D. «A Solar Irradiance Climate Data Record». Bulletin of the American Meteorological Society, 97, 7, 22-08-2016, pàg. 1265–1282. Bibcode: 2016BAMS...97.1265C. DOI: 10.1175/bams-d-14-00265.1.
- ↑ «Introduction to Solar Radiation». Newport Corporation. Arxivat de l'original el 29 octubre 2013.
- ↑ Michael Allison; Robert Schmunk. «Technical Notes on Mars Solar Time». NASA, 05-08-2008. [Consulta: 16 gener 2012].
- ↑ «Solar and Wind Energy Resource Assessment (SWERA) | Open Energy Information».
- ↑ Nonnenmacher, Lukas; Kaur, Amanpreet; Coimbra, Carlos F.M. «Verification of the SUNY direct normal irradiance model with ground measurements» (en anglès). Solar Energy, 99, 01-01-2014, pàg. 246–258. Bibcode: 2014SoEn...99..246N. DOI: 10.1016/j.solener.2013.11.010. ISSN: 0038-092X.
- ↑ «Determining your solar power requirements and planning the number of components».
- ↑ «Heliostat Concepts». redrok.com.
- ↑ Convertit a base anual de «Optimum Tilt of Solar Panels», 2017.
- ↑ [2] Arxivat July 14, 2014, a Wayback Machine.
- ↑ «How Do Solar Panels Work?». Arxivat de l'original el 15 octubre 2004. [Consulta: 21 abril 2018].
- ↑ Nall, D. H. «Looking across the water: Climate-adaptive buildings in the United States & Europe». The Construction Specifier, 57, 2004–11, pàg. 50–56. Arxivat de l'original el 2009-03-18.
- ↑ Han, Di; Fei, Jipeng; Li, Hong; Ng, Bing Feng «The criteria to achieving sub-ambient radiative cooling and its limits in tropical daytime». Building and Environment, 221, 1, 8-2022, pàg. 109281. DOI: 10.1016/j.buildenv.2022.109281.
- ↑ Munday, Jeremy «Tackling Climate Change through Radiative Cooling». Joule, 3, 9, 2019, pàg. 2057–2060. DOI: 10.1016/j.joule.2019.07.010.
- ↑ Chen, Meijie; Pang, Dan; Chen, Xingyu; Yan, Hongjie; Yang, Yuan «Passive daytime radiative cooling: Fundamentals, material designs, and applications». EcoMat, 4, 2022. DOI: 10.1002/eom2.12153.
Bibliografia
[modifica]- Willson, Richard C.; H.S. Hudson «The Sun's luminosity over a complete solar cycle». Nature, 351, 6321, 1991, pàg. 42–4. Bibcode: 1991Natur.351...42W. DOI: 10.1038/351042a0.
- «The Sun and Climate». U.S. Geological Survey Fact Sheet 0095-00. [Consulta: 21 febrer 2005].
- Foukal, Peter; etal «The effects of sunspots and faculae on the solar constant». Astrophysical Journal, 215, 1977, pàg. 952. Bibcode: 1977ApJ...215..952F. DOI: 10.1086/155431.
- Stetson, H.T.. Sunspots and Their Effects. Nova York: McGraw Hill, 1937.
- Yaskell, Steven Haywood. [Irradiància solar a Google Books Grand Phases On The Sun: The case for a mechanism responsible for extended solar minima and maxima]. Trafford Publishing, 31 desembre 2012. ISBN 978-1-4669-6300-9.


















![{\displaystyle {\begin{aligned}\int _{\pi }^{-\pi }Q\,dh&=\int _{h_{o}}^{-h_{o}}Q\,dh\\&=S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\int _{h_{o}}^{-h_{o}}\cos(\Theta )\,dh\\&=S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h)\right]_{h=h_{o}}^{h=-h_{o}}\\&=-2S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcb1dbb45713cbc7a95e25fce752e4807f05f67e)
![{\displaystyle {\overline {Q}}^{\text{dia}}={\frac {S_{o}}{\pi }}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2addc9494530f2887aae0a0da3979096f7638599)