Matriu de substitució

En termes de bioinformàtica i biologia evolutiva, una matriu de substitució descriu la velocitat a la qual un caràcter en una seqüència de nucleòtids o en una seqüència de proteïnes és canviat per altres caràcters al llarg del temps evolutiu. Els valors representats en aquesta matriu contenen el valor logarítmic associat cada mutació, és a dir la propensió de cada tipus de mutació a ser acceptada o rebutjada evolutivament. Per tant, és una aplicació d'una matriu estocàstica on veiem la possibilitat que un nucleòtid o un aminoàcid es transformi en un altre en un temps determinat.

Les matrius de substitució se solen veure en el context d'alineaments de seqüències d'aminoàcids o d'ADN, on la similitud entre seqüències depèn del seu temps de divergència i de les taxes de substitució representades a la matriu.^[1]

Antecedents

En el procés d'evolució, d’una generació a la següent les seqüències d’aminoàcids de les proteïnes d’un organisme s’alteren gradualment mitjançant l’acció de les mutacions de l’ADN. Per exemple, en les dues imatges inferiors es pot observar una mutació puntual en una seqüència d'ARN. La diferència entre aquestes mutacions és que en la primera seqüència la mutació origina un canvi d'aminoàcid (mutació no sinònima) i en la segona no esdevé aquest canvi (mutació sinònima). El fet que la mutació puntual no provoqui un canvi d'aminoàcid es deu principalment a la redundància del codi genètic, que tradueix codons similars en aminoàcids similars. Aquestes mutacions es poden incrementar durant un període evolutiu més llarg.^[2]

Tendència d'un aminoàcid a mutar

Cada aminoàcid és més o menys propens a mutar en altres aminoàcids, a causa de les diferents propietats químiques i físiques. Per tal de comparar la tendència a mutar dels diferents aminoàcids d'acord amb les seves característiques químiques es pot utilitzar el Diagrama de Venn.^[3] Aquest conté els vint aminoàcids agrupats en cinc clústers diferents; entre aminoàcids que pertanyen al mateix grup (propietats químiques semblants), és més fàcil que es produeixin mutacions respecte als que formen part de grups diferents (químicament desiguals). Per exemple, un residu hidrofílic com l'arginina és més probable que es substitueixi per un altre residu hidròfil com la glutamina que no pas que es transformi en un residu hidrofòbic com la leucina. A més, mutar un aminoàcid en un residu amb propietats significativament diferents podria afectar el plegament i / o l’activitat de la proteïna. És probable que aquest tipus de substitució disruptiva s’elimini de les poblacions mitjançant l’acció de la selecció natural. Això és degut al fet que aquesta substitució té una major probabilitat de fer que una proteïna no funcioni o que formi agregats sent així tòxica per a l'organisme.^[1]

Alineament de seqüències

En presència de dues seqüències d'aminoàcids s'hauria de poder predir si aquestes provenen d'un avantpassat comú o no. Per tal de poder-ho determinar, és necessari alinear les seqüències mitjançant mètodes computacionals, per tal de veure el percentatge d'homologia que presenten i determinar quin alineament és més correcte. Si el percentatge d'aquest l'alineament supera el 30% d'identitat i les seqüències són més llargues a 100 aminoàcids, es podrà determinar que aquestes presenten un avantpassat comú. Per realitzar aquestes comparacions entre dues seqüències és necessari saber quant costa substituir cada parella d'aminoàcids, és a dir, es necessita tenir la capacitat per assignar un cost a cada una d’aquestes substitucions. Per això es construeix una matriu de 20x20 aminoàcids on l'entrada $(i,j)$ és igual a la probabilitat que l'aminoàcid $i$ es transformi en l'aminoàcid $j$ en un determinat temps evolutiu. Hi ha moltes maneres diferents de construir aquesta matriu, anomenada matriu de substitució. Aquests són els més utilitzats:

Matriu d'identitat

La matriu de substitució més senzilla possible seria aquella en què cada aminoàcid es considera el màxim semblant de si mateix, però no és capaç de transformar-se en cap altre aminoàcid. Aquesta matriu semblaria:

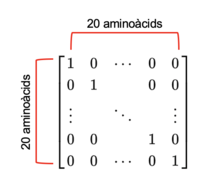
Aquesta matriu d’identitat tindrà èxit en l’alineació de seqüències d’aminoàcids molt similars. En canvi, no tindria èxit en alinear dues seqüències llunyanament relacionades, ja que en aquestes els aminoàcids tendiran a ser més diferents entre si. Per aquest motiu, s'han d’esbrinar totes les probabilitats de substitució d’una manera més rigorosa.^[4]

Matrius de log-odds

Com que les matrius d’identitat no són prou rigoroses és necessari utilitzar un altre tipus de matrius de substitució anomenades matrius de log-odds. Aquestes resulten d'un examen empíric de seqüències prèviament alineades i s'expressen les probabilitats de transformació en el que s’anomena puntuacions log-odds. La matriu de puntuacions S es defineix com:

S_{i},_{j}=\log {p_{i}*M_{i},_{j} \over p_{i}*p_{j}}=\log {M_{i},_{j} \over p_{j}}=\log {freq.observada \over freq.esperada}

on $M_{i},_{j}$ és la probabilitat que l’aminoàcid $i$ es transforma en aminoàcid $j$ , i $p_{i},p_{j}$ són les freqüències dels aminoàcids $i$ i $j$ . És a dir, comparen la probabilidad de que s'hagi produit un canvi de l'aminoàcid $i$ pel $j$ , respecte a la probabilitat de trobar aquest aminoàcid $j$ a atzar. Es treballa en una escala logarítmica a causa de les propietats d'aquests, que permeten construir una escala numèrica simètrica:

Si el valor obtingut és positiu, significa que la mutació tendeix a ser favorable evolutivament.
Si el valor obtingut és negatiu, significa que la mutació tendeix a no ser favorable evolutivament.
Si el valor obtingut és 0, significa que l'observat és igual a l'esperat i per tant la selecció no intervé.^[4]

PAM

Història

Les matrius PAM són unes de les primeres matrius de substitució d’aminoàcids, que va ser desenvolupada per Margaret Dayhoff als anys setanta. Aquesta fisicoquímica pionera en el camp de la bioinformàtica va agafar 71 parells de proteïnes petites, globulars i fàcils d’alinear ja eren un 85% idèntiques. Les va alinear i observant les diferències entre aquestes proteïnes estretament relacionades, va comptar les mutacions que hi havia en els diferents alineaments. Com que va utilitzar homòlegs molt relacionats per a observar els diferents canvis, no s’espera que les mutacions observades canviïn significativament les funcions comunes de les proteïnes. Per tant, les substitucions observades són aquelles que es consideren acceptades per selecció natural, és a dir, les diferències s’observen a regions degenerades.

Unitat PAM

PAM és una unitat de la distància evolutiva que hi ha entre dues seqüències d’aminoàcids. 1 PAM és una mutació puntual acceptada per cada 100 aminoàcids, que és el mateix que 300 nucleòtids.^[5]

$PAM={mutacions \over 300nt}$

Creació de la matriu PAM

Per crear una matriu de substitució de PAM1, es tria un grup de seqüències molt relacionades amb freqüències de mutació corresponents a una unitat de PAM.

A partir de les dades mutacionals recollides d’aquest grup de seqüències, es pot obtenir una matriu de substitució PAM1. Aquesta matriu estima quina taxa de substitució s’esperaria si s’hagués canviat l’1% dels aminoàcids. La matriu PAM1 s’utilitza com a base per al càlcul de les altres matrius assumint que les mutacions repetides seguirien el mateix patró que les de la matriu PAM1 i que es poden produir múltiples substitucions al mateix lloc. Utilitzant aquesta lògica, Dayhoff va derivar matrius tan altes com PAM250. Es pot calcular una matriu per a seqüències més llunyanes relacionades a partir d’una matriu per a seqüències estretament relacionades prenent la segona matriu a una potència. Per exemple, podem aproximar aproximadament la matriu WIKI2 de la matriu WIKI1 dient que $W_{2}=W_{1}^{2}$ on $W_{1}$ és WIKI1 i $W_{2}$ és WIKI2. Així es calcula la matriu PAM250.

Si 2 seqüències divergeixen en 250 PAM, significa que aproximadament presenten un 17% de semblança. Tot i que si s’observen 75 mutacions puntuals i en canvi la PAM és de 250 és perquè moltes d’aquestes mutacions han estat en les mateixes posicions. Per tant hi ha mutacions que són invisibles perquè han esdevingut en un lloc que ja havia estat mutat, és a dir, en la mateixa posició que una mutació anterior.

Hi ha un procés matemàtic que permet fer la correcció entre les mutacions que realment han ocorregut (PAM) i les mutacions mesurades en l'alineament de seqüències (diferències observades). Justament aquest valor real de mutacions esdevingudes (PAM) és el necessari per a reconstruir arbres filogenètics.

Aquest factor de correcció és fàcil d’aplicar en un inici quan la seqüència no es troba en un estat de saturació. Però si la seqüència se satura dona lloc al mateix nombre de mutacions observades tant si fa 3 bilions d’anys que les proteïnes es van separar com si fa només 1 bilió d’anys; serà per tant impossible de reconstruir en el temps aquest alineament. Per tant, en aquest estat de saturació hi ha una tendència a desestimar el nombre de mutacions totals que ocorren, és a dir la PAM.

La diagonal de qualsevol matriu de substitució indica com de conservat tendeix a estar un residu, ja que és on aquest apareix alineat amb si mateix. Per exemple en el cas del triptòfan (W) en la PAM250 s’observa que té la major puntuació, concretament de 17. Això vol dir que el triptòfan està molt conservat i que la majoria de les vegades s’observa un triptòfan alineat amb un altre triptòfan. Estadísticament, de forma biològica aquest residu es troba molt conservat ja que, és l’aminoàcid més gran i manté la forma de la proteïna. Alguns residus són més fàcils d’estar modificats que i això s’observa perquè aquests tenen les mateixes puntuacions si s’intercanvien per ells mateixos o que si ho fan per un altre aminoàcid dins de la matriu. Com veiem en la PAM250 la valina (V), es pot modificar fàcilment per altres aminoàcids. Canviar una valina per la seqüència la isoleucina (I) té el mateix cost que no canviar-la (és a dir són pràcticament idèntiques), concretament en aquesta matriu té una puntuació de 4.^[6]

Limitacions de PAM

Aquest model funciona força bé per a seqüències curtes, però presenta alguns problemes:

El model PAM assumeix que tots els residus són igualment mutables.
El model PAM ha estat fet a partir de les posicions més mutables en comptes de partir de les posicions més conservades, que són les que reflecteixen les propietats químiques i estructurals importants.
Deriven d’un set de seqüències molt antigues: de petites proteïnes globulars que ja es trobaven a la base de dades el 1978. Aquestes proteïnes globulars tan petites no tenen la mateixa evolució que d’altres, com per exemple les proteïnes transmembrana.
En la PAM hi ha molt poca influència del codi genètic, el que significa és que els residus que tenen una composició semblant del codi genètic (mateixa composició de triplets per formar proteïnes), tenen una major probabilitat de ser mutats l’un per l’altre.^[5]

BLOSUM

La metodologia de Dayhoff per comparar espècies estretament relacionades va resultar no ser útil per alinear seqüències evolutivament divergents. Utilitzant les matrius PAM es realitza una extrapolació on a partir de comparar seqüències estretament relacionades es pretén inferir en la comparació de seqüències llunyanes. Això suposa un error que es pot solucionar amb l'aplicació de la sèrie de matrius BLOSUM (BLOck SUbstitution Matrix).

Creació de la matriu BLOSUM

Steven Henikoff I Jorja Henikoff van construir aquestes matrius utilitzant múltiples alineacions de proteïnes evolutivament divergents. Per tal de construir aquestes matrius van escanejar la base de dades "BLOCKS" que es va generar des de múltiples segments de seqüències alineades provinents de Prosite sense buits. Aquestes estaven agrupades en blocs amb una similitud de seqüència inferior a un llindar. Les seqüències que són idèntiques en més d’un tant per cent s’eliminen per evitar biaixos a causa de la presència excessiva de certes proteïnes a la base de dades. Se suposa que aquestes seqüències conservades tenen una importància funcional dins de les proteïnes relacionades i, per tant, tindran taxes de substitució més baixes que les regions menys conservades.

Per a la matriu BLOSUM62, aquest llindar es va establir en el 62%, mesurant només la substitució de seqüències de proteïnes que tenen un màxim 62% de similitud. S’utilitzaria una matriu BLOSUM amb un llindar elevat (BLOSUM80) per alinear dues seqüències estretament relacionades i amb un llindar inferior (BLOSUM45) per a seqüències més divergents. Resulta que la matriu BLOSUM62 realitza un treball excel·lent detectant similituds en seqüències llunyanes, i aquesta és la matriu que s’utilitza per defecte en les aplicacions d’alineació més recents, com ara BLAST.^[7]

Diferències entre PAM i BLOSUM

Les matrius PAM es basen en un model evolutiu explícit, mentre que les matrius BLOSUM es basen en un model implícit d'evolució.
Les matrius PAM es basen en mutacions observades al llarg d’un alineament global, que inclou regions molt conservades i altament mutables. Les matrius BLOSUM es basen només en regions molt conservades en sèries d'alineacions sense buits, per tant es basen en alineaments locals.
El mètode utilitzat per comptar les substitucions és diferent: a diferència de la matriu PAM, el procediment BLOSUM utilitza grups de seqüències en què no totes les mutacions es compten igual.
Els números més alts en l'esquema de denominació de la matriu PAM denoten una distància evolutiva més gran, mentre que els números més grans en l'esquema de denominació de la matriu BLOSUM denoten una semblança de seqüència més gran i, per tant, una distància evolutiva menor. Per exemple PAM150 s'utilitza per a seqüències més llunyanes que PAM100; BLOSUM62 s’utilitza per a seqüències més properes que BLOSUM50.^[6]

Limitacions

La principal limitació és que les matrius de substitució ignoren les interaccions no locals i assumeixen que residus idèntics són iguals. Les matrius de substitució entenen que cada aminoàcid és independent, i obvien les seves interaccions. Un cop la proteïna està plegada (estructura 3D), els residus no només interaccionen amb els dels seus costats (locals). La matriu de substitució assumeix que cada aminoàcid és independent dels seus veïns i que el cost de substitució d’aquest aminoàcid no depèn de les interaccions que estigui establint. També assumeixen que la taxa d’evolució és constant, que és la mateixa per tots els nucleòtids de la proteïna. Sabem que això no és cert, els residus de dins de la proteïna tendeixen a evolucionar de forma més lenta que els aminoàcids localitzats a la part de fora de la proteïna. A més, quan s’observen els canvis en una seqüència d’una proteïna no s’està mirant tota la proteïna sencera, per tant, les matrius de substitució no són sempre informatives. Finalment, en un alineament per parelles no es pot saber quin aminoàcid és ancestral, per saber-ho caldria conèixer la seqüència de la proteïna de l’antecessor comú de les dues espècies. Per això en la matriu de substitució el que hi ha és una mitjana del cost dels dos canvis, una puntuació bidireccional. Per exemple s’ha de tenir en compte que el cost de canviar una glicina per un triptòfan no és el mateix que per canviar un triptòfan en una glicina (i això passa amb tots els aminoàcids).^[6]

Ampliacions i millores

S’han desenvolupat moltes matrius de substitució especialitzades que descriuen les taxes de substitució d’aminoàcids en contextos estructurals o de seqüència específics, com en les hèlixs alfa transmembrana,^[8] per a combinacions d’estructura secundària i d’accessibilitat de dissolvents ^[9]^[10]^[11] o per a contextos d’estructura de seqüències locals.^[11] Aquestes matrius de substitució específiques creades en funció del context on es localitzen els diferents aminoàcids condueixen a una qualitat de l'alineament generalment millorada. Tot i això aquestes matrius específiques presenten a un cert cost de velocitat, és a dir, triguen més a fer els càlculs computacionals i per aquest motiu encara no s'utilitzen àmpliament. Recentment, s’han derivat semblances d’aminoàcids específics del context de seqüències que no necessiten matrius de substitució, sinó que depenen d’una biblioteca de contextos de seqüència. Utilitzant aquesta idea, ha sorgit una extensió de BLAST on es té en compte el context on es troba cada residu. Aquest últim ha demostrat que aconsegueix una doble millora de la sensibilitat per seqüències remotament relacionades i treballa a velocitats similars (CS-BLAST).

Terminologia

Tot i que "matriu de transició" s'utilitza sovint indistintament amb "matriu de substitució" en camps diferents de la bioinformàtica, el terme anterior és problemàtic en bioinformàtica. Pel que fa a les substitucions de nucleòtids, "transició" també s'utilitza per indicar aquelles substitucions que es troben entre les purines de dos anells (A → G i G → A) o que es troben entre les pirimidines d'un anell (C → T i T → C). Com que aquestes substitucions no requereixen un canvi en el nombre d'anells, es produeixen amb més freqüència que les altres substitucions. "Transversió" és el terme que s'utilitza per indicar les substitucions de menor velocitat que canvien una purina a pirimidina o viceversa (A ↔ C, A ↔ T, G ↔ C i G ↔ T).

Vegeu també

Models d'evolució de l'ADN

Referències

↑ ^1,0 ^1,1 Patthy, László.. Protein evolution. 2a edició. Malden, MA: Blackwell Science, 2008. ISBN 978-1-4051-5166-5.
↑ Chen, Hanbo; Boutros, Paul C. «VennDiagram: a package for the generation of highly-customizable Venn and Euler diagrams in R». BMC Bioinformatics, 12, 1, 26-01-2011, pàg. 35. DOI: 10.1186/1471-2105-12-35. ISSN: 1471-2105. PMC: PMC3041657. PMID: 21269502.
↑ Wiley Series on Bioinformatics: Computational Techniques and Engineering. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2007-08-09, p. 501–501. ISBN 978-0-470-25344-1.
↑ ^4,0 ^4,1 Durbin, Richard; Eddy, Sean R.; Krogh, Anders; Mitchison, Graeme. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, 1998-04-23. DOI 10.1017/cbo9780511790492. ISBN 978-0-521-62041-3.
↑ ^5,0 ^5,1 «On the PAM matrix model of protein evolution.». Molecular Biology and Evolution, 9-1985. DOI: 10.1093/oxfordjournals.molbev.a040360. ISSN: 1537-1719.
↑ ^6,0 ^6,1 ^6,2 Mount, D. W. «Using BLOSUM in Sequence Alignments» (en anglès). Cold Spring Harbor Protocols, 2008, 6, 01-06-2008, pdb.top39–pdb.top39. DOI: 10.1101/pdb.top39. ISSN: 1559-6095.
↑ Muller, T.; Rahmann, S.; Rehmsmeier, M. «Non-symmetric score matrices and the detection of homologous transmembrane proteins». Bioinformatics, 17, Suppl 1, 01-06-2001, pàg. S182–S189. DOI: 10.1093/bioinformatics/17.suppl_1.s182. ISSN: 1367-4803.
↑ Rice, Danny W.; Eisenberg, David «A 3D-1D substitution matrix for protein fold recognition that includes predicted secondary structure of the sequence» (en anglès). Journal of Molecular Biology, 267, 4, 4-1997, pàg. 1026–1038. DOI: 10.1006/jmbi.1997.0924.
↑ Gong, Sungsam; Blundell, Tom L. «Discarding Functional Residues from the Substitution Table Improves Predictions of Active Sites within Three-Dimensional Structures» (en anglès). PLoS Computational Biology, 4, 10, 03-10-2008, pàg. e1000179. DOI: 10.1371/journal.pcbi.1000179. ISSN: 1553-7358. PMC: PMC2527532. PMID: 18833291.
↑ Goonesekere, Nalin C. W.; Lee, Byungkook «Context-specific amino acid substitution matrices and their use in the detection of protein homologs: Context-Specific Substitution Matrices» (en anglès). Proteins: Structure, Function, and Bioinformatics, 71, 2, 01-05-2008, pàg. 910–919. DOI: 10.1002/prot.21775.
↑ ^11,0 ^11,1 Huang, Y.-m.; Bystroff, C. «Improved pairwise alignments of proteins in the Twilight Zone using local structure predictions» (en anglès). Bioinformatics, 22, 4, 15-02-2006, pàg. 413–422. DOI: 10.1093/bioinformatics/bti828. ISSN: 1367-4803.

[:02-1] 1,0 ^1,1 Patthy, László.. Protein evolution. 2a edició. Malden, MA: Blackwell Science, 2008. ISBN 978-1-4051-5166-5.

[2] Chen, Hanbo; Boutros, Paul C. «VennDiagram: a package for the generation of highly-customizable Venn and Euler diagrams in R». BMC Bioinformatics, 12, 1, 26-01-2011, pàg. 35. DOI: 10.1186/1471-2105-12-35. ISSN: 1471-2105. PMC: PMC3041657. PMID: 21269502.

[3] Wiley Series on Bioinformatics: Computational Techniques and Engineering. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2007-08-09, p. 501–501. ISBN 978-0-470-25344-1.

[:22-4] 4,0 ^4,1 Durbin, Richard; Eddy, Sean R.; Krogh, Anders; Mitchison, Graeme. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, 1998-04-23. DOI 10.1017/cbo9780511790492. ISBN 978-0-521-62041-3.

[:12-5] 5,0 ^5,1 «On the PAM matrix model of protein evolution.». Molecular Biology and Evolution, 9-1985. DOI: 10.1093/oxfordjournals.molbev.a040360. ISSN: 1537-1719.

[:32-6] 6,0 ^6,1 ^6,2 Mount, D. W. «Using BLOSUM in Sequence Alignments» (en anglès). Cold Spring Harbor Protocols, 2008, 6, 01-06-2008, pdb.top39–pdb.top39. DOI: 10.1101/pdb.top39. ISSN: 1559-6095.

[7] Muller, T.; Rahmann, S.; Rehmsmeier, M. «Non-symmetric score matrices and the detection of homologous transmembrane proteins». Bioinformatics, 17, Suppl 1, 01-06-2001, pàg. S182–S189. DOI: 10.1093/bioinformatics/17.suppl_1.s182. ISSN: 1367-4803.

[8] Rice, Danny W.; Eisenberg, David «A 3D-1D substitution matrix for protein fold recognition that includes predicted secondary structure of the sequence» (en anglès). Journal of Molecular Biology, 267, 4, 4-1997, pàg. 1026–1038. DOI: 10.1006/jmbi.1997.0924.

[9] Gong, Sungsam; Blundell, Tom L. «Discarding Functional Residues from the Substitution Table Improves Predictions of Active Sites within Three-Dimensional Structures» (en anglès). PLoS Computational Biology, 4, 10, 03-10-2008, pàg. e1000179. DOI: 10.1371/journal.pcbi.1000179. ISSN: 1553-7358. PMC: PMC2527532. PMID: 18833291.

[10] Goonesekere, Nalin C. W.; Lee, Byungkook «Context-specific amino acid substitution matrices and their use in the detection of protein homologs: Context-Specific Substitution Matrices» (en anglès). Proteins: Structure, Function, and Bioinformatics, 71, 2, 01-05-2008, pàg. 910–919. DOI: 10.1002/prot.21775.

[Ref-11] 11,0 ^11,1 Huang, Y.-m.; Bystroff, C. «Improved pairwise alignments of proteins in the Twilight Zone using local structure predictions» (en anglès). Bioinformatics, 22, 4, 15-02-2006, pàg. 413–422. DOI: 10.1093/bioinformatics/bti828. ISSN: 1367-4803.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]