Parell cinemàtic

Alguns tipus d'unions entre peces.

En enginyeria mecànica, un parell cinemàtic és una unió entre dos membres d'un mecanisme. Un exemple són dues barres unides per un pern (unió anomenada articulació, fig. 2) que permet que les peces girin al voltant del pern.

Els parells cinemàtics es classifiquen en diferents tipus segons el moviment que permeten, i són un element cabdal en la construcció d'un mecanisme, ja que defineixen el tipus de moviment que hi haurà entre les peces unides.

Tipus de parells cinemàtics

Guia lliscant cilíndrica

En dues dimensions

Per a mecanismes plans, és a dir, que executen un moviment en un pla, alguns exemples de parells cinemàtics són:

• L'articulació, que elimina el desplaçament de translació relatiu de dos sòlids obligant permanentment al fet que dos punts geomètrics dels dos sòlids ocupin contínuament la mateixa posició. No obstant això, l'articulació no impedeix la reorientació o gir relatiu d'un sòlid respecte a l'altre.
• La guia corredissa, que elimina un grau de llibertat de translació i la possibilitat de reorientació d'un sòlid respecte a un altre.

En tres dimensions

En general :

• L'articulació cilíndrica, que elimina tots els graus de llibertat excepte la possibilitat de rotació d'un sòlid respecte a l'altre al voltant d'un cert eix de gir, elimina cinc graus de llibertat.
• La ròtula esfèrica, que permet qualsevol gir o canvi d'orientació d'un sòlid respecte a un altre, però impedeix la seva translació relativa, per la qual cosa sempre un punt geomètric de tots dos sòlids és comú, elimina tres graus de llibertat.
• Guia lliscant cilíndrica, permet la translació relativa i el gir al voltant d'un eix, elimina per tant quatre graus de llibertat.
• Guia lliscant no cilíndrica, permet la translació relativa segons un eix però no el gir al voltant del mateix, elimina per tant cinc graus de llibertat.
*La soldadura elimina tots els graus de llibertat d'un sòlid respecte a un altre, per la qual cosa dos sòlids soldats cinemàticament poden considerar-se un únic sòlid, és a dir, elimina sis graus de llibertat.

Rodament

Una connexió articulada s'anomena suport si un dels dos cossos està fermament connectat a l'estructura de la màquina o a la fonamentació i, per tant, està en repòs. A diferència d'una articulació, un rodament no sol formar part d'un mecanisme més complex (engranatge). En el primer pla de la seva consideració hi ha gairebé sempre només l'únic tipus de connexió mòbil que hi té lloc. Els semieixos giratoris i els cossos desplaçables linealment (rodaments lineals) es munten en màquines i dispositius, bigues de ponts a la indústria de la construcció o altres estructures suportades puntuals. En els aparells de suport en estructures, a diferència dels de màquines i dispositius, només es produeixen moviments molt petits (canvis i rotacions). Només serveixen per crear rodaments determinats estàticament i per mantenir-los en cas de pertorbacions (enfonsament, canvis de longitud relacionats amb la temperatura, etc.).

En lloc de coixinets llisos, els rodaments de rodets amb elements rodants inserits entre els elements d'unió s'utilitzen sovint com a coixinets en màquines i dispositius. Aquests també corresponen a les formes bàsiques de les juntes juntes giratòries i de tall, mentre que les anomenades "juntes rodants" utilitzades en la construcció com a coixinets en la seva forma bàsica juntes corbes (quan s'aparella formigó amb formigó, només és possible rodar).

Elements de màquines

Junta universal

Muntatge cardànic de la brúixola de vaixell. L'anell més extern està fermament unit al vaixell. Les extensions en forma de coixinet del cercle exterior són una indicació de l'escorça del vaixell; altrament, són verticals.

Articulació cardànica com a element de màquina per a connexió a dos eixos contrarrotatius.
L'adaptador, juntament amb els pivots, té forma de creu.
Els eixos de totes les articulacions es troben en un punt. La caixa d'engranatges de quatre parts obtinguda amb les juntes de coixinet de l'eix (no mostrades) i el bastidor de la màquina és esfèric).

La junta universal o cardan és una sèrie de dues juntes rotatives. La segona superfície de contacte de cadascuna de les dues juntes es troba a la peça intermèdia comuna en forma de creu (vegeu la figura de la dreta). Els eixos de les juntes giratòries es tallen a 90°. El punt d'intersecció és el punt de pivot en què els dos "vastacs" d'articulació disposats en angle recte respecte de l'eix d'articulació de pivot respectiu poden pivotar entre si. L'articulació cardànica té dos graus de llibertat de moviment. En comparació amb la ròtula, no té la llibertat de rotació dels fills de l'articulació al voltant del seu propi eix. El seu grau de llibertat és f=2.

L'aplicació històricament més antiga va ser el cardan, en què és possible el pivot sobre els dos eixos espacials horitzontals, però no es permet la rotació sobre l'eix vertical. La peça intermèdia és un anell.

La manca de llibertat de rotació al voltant dels plançons de la junta també fa que la junta universal sigui adequada per a la transmissió de parell entre eixos que poden pivotar un contra un altre (eix cardan).

Juntes de velocitat constant

Igual que la junta universal, les juntes homocinètiques s'utilitzen per a la transmissió de parell entre eixos que poden girar en adreces oposades. No tenen l'inconvenient de no ser completament sincrònics, sinó que fluctuen periòdicament amb la rotació. Com la junta universal, són ròtules reduïdes a dos moviments giratoris a l'exterior. A l'interior, igual que a la junta universal, també hi ha peces intermèdies els elements d'unió de les quals estan en contacte amb superfícies de boles o casquets variats. En el cas de la "junta Rzeppa", per exemple, les boles estan en contacte amb superfícies esfèriques acanalades.

Articulacions elàstiques en enginyeria mecànica

Les juntes de ressort no pertanyen a les formes bàsiques de juntes ni als camps en què els cossos rígids llisquen i/o roden els uns sobre els altres. Estan disponibles com a juntes giratòries i lliscants aproximades amb poca mobilitat. Un cos que cedeix elàsticament, per exemple una vareta de ressort que està torçada o doblegada, instal·lada permanentment. Les juntes de ressort tenen l'avantatge d'estar lliures de fricció, de joc i de manteniment.

Les juntes de ressort de torsió s'usen sovint en instruments de mesura mecànics, on el moment de torsió es pot fer servir com un moment de restauració.

Si la junta de ressort no es realitza amb un component separat sinó amb un debilitament local del mateix component, això s'anomena junta de flexió.

Articulació de direcció

Connexió lliscant

La connexió lliscant modela un contacte cilíndric que no és de revolució (és a dir, generat per translació).

La connexió lliscant proporciona cinc graus de connexió en permetre únicament el moviment de translació a la direcció de la connexió. La definició d'aquesta connexió ha d'especificar aquesta adreça.

Hi ha diversos enfocaments possibles per a realitzar aquesta connexió:

• a partir d'un suport pla (3 graus de connexió): s'afegeix un segon pla de contacte, assecant amb el primer o, més senzillament, un eix guia lateral (connexió lineal recta) paral·lel al pla;
• a partir d'una connexió pivotant lliscant (4 graus de connexió): n'hi ha prou amb una connexió puntual que impedeixi la rotació, el que s'anomena "antigir" (generalment 2 punts oposats).

A nivell més tecnològic, es pot considerar el caràcter bilateral d'aquesta connexió. Per exemple, els calaixos d'una còmoda estan guiats bilateralment, mentre que la via del ferrocarril ofereix una connexió unilateral en sentit vertical.

Aquesta és la connexió proporcionada en una transmissió per eix. Ranura que modela el guiatge de la corredissa d'un trombó o el pistó d'una trompeta.

A diferència del moviment de rotació de la baula pivotant, l'amplitud de la translació possible està limitada per les dimensions de les peces. Quan el calaix està totalment estès, la baula ja no existeix! La modelització matemàtica no té en compte els límits de la guia.

• 
  La solució més òbvia, però no per això menys hiperestàtica.
• 
  La corredissa d'un trombó està unida al cos de l'instrument per una corredissa, combinant dos pivots lliscants amb eixos paral·lels (solució hiperestàtica).
• 
  Connexió cua de milà per a una connexió bilateral.
• 
  5 punts = lliscament

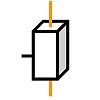
Lliscament de direcció X				Unions : Ty = 0 Tz = 0 Rx = 0 Ry = 0 Rz = 0	Llibertat : Tx

Quan dos sòlids estan en una connexió lliscant, hi ha almenys dues línies estrictament paral·leles comunes a tots dos sòlids, la direcció dels quals defineix l'única característica geomètrica de la connexió.

Per error, a aquesta connexió se li assigna un eix. Si bé és cert que les solucions utilitzades per realitzar aquesta connexió solen incloure plànols o eixos de simetria, la seva definició geomètrica no els necessita.

Atès que la mobilitat dels objectes no es pot comparar a la dels objectes col·locats en una pista de patinatge que permet un lliscament gairebé ideal, les consideracions menys teòriques d'enllaços mecànics amb fregament condueixen a l'embús per arc. Això demostra que la disposició de la càrrega pel que fa a les superfícies de contacte influeix (tribologia).

Connexió plana o pla/pla

La connexió plana (de vegades anomenada incorrectament connexió plana de suport, que és un terme utilitzat per descriure el contacte) té 3 graus de connexió. Obliguen el moviment a romandre en un pla. Les dues translacions i la rotació en aquest pla són lliures.

Aquesta connexió s'obté naturalment pressionant dues superfícies planes una contra l'altra. De forma més general, només cal que el contacte entre dos sòlids es produeixi en almenys 3 punts no alineats amb normals en la mateixa adreça. Aquesta és la base dels anomenats enllaços prismàtics. La direcció comuna de les normals dels contactes elementals dona la "direcció principal de la unió".

El suport de les tres potes d'un tamboret sobre un terra pla constitueix una connexió plana. La quarta pota d'una cadira només toca el terra si els extrems de les potes són perfectament coplanaris; el sistema és llavors hiperestàtic els enllaços superen en nombre a la necessitat de guia.

• 
  Dues cares planes en suport.
• 
  Exemples de suports plans
• 
  Un tamboret de tres potes mai no trontolla: solució isostàtica.
• 
  3 punts = suport pla

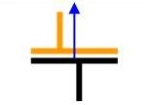
Suport pla de normal Z		no normalitzat		Enllaços : Tz = 0 Rx = 0 Ry = 0	Llibertat : Tx, Ty Rz

Els punts de contacte no són necessàriament al mateix pla. Per exemple, si escurceu una pota d'una cadira, la podeu col·locar en una escala, amb la pota més curta recolzada en un esglaó superior. Com que les normals són paral·leles, el conjunt és sempre una connexió plana.

Quan dos sòlids estan en contacte pla, almenys un pla coincideix amb un pla de l'altre.

Connexions d'eixos

Unió pivotant

La unió pivotant és el tipus de connexió més utilitzat als sistemes mecànics. Guia una peça en rotació permetent un únic gir al voltant de l'eix de la connexió.

La definició d'aquesta unió ha d'especificar "la posició del vostre eix", és a dir, una línia recta com en el cas d'un pivot lliscant. En el cas d'una porta, la posició de les frontisses determina el sentit de la seva obertura; de la mateixa manera, la porta del darrere d'un cotxe està guiada per un pivot horitzontal situat a la part superior. Si fos a la part inferior, el resultat seria una porta forçada. Per tant, la precisió de la direcció per si sola és insuficient.

Els dissenys més habituals es basen a completar un contacte cilíndric amb un topall axial: sovint es tracta d'un pla normal a l'eix (pivot lliscant + suport pla: solució hiperestàtica); en aquest cas, es distingeix entre pivots amb predomini cilíndric (en el cas d'una roda unida per un coixinet llis com en un carretó) o pla (en el cas d'una tapa). L'ideal és combinar un pivot lliscant amb una connexió puntual.

Aquesta unió també es pot obtenir combinant una unió lineal anular i una ròtula; un esquema que es troba en certes guies de rodament de boles amb topall sobre un coixinet.

En el cas de les unions pivotants, sobretot pel que fa al bloqueig de la translació axial, es distingeix entre unions unilaterals i bilaterals, segons s'elimini aquest grau de llibertat en un sentit o en tots dos. Si per a una porta la solució unilateral n'hi ha prou, cal subjectar la roda d'un vehicle en tots dos sentits. Aquest enfocament és, per descomptat, tecnològic i no fa referència a aquest assumpte.

• 
  Connexió pivot per cilindre i pla radial (solució hiperestàtica i unilateral)
• 
  Solucions constructives bilaterals per unir claus d'un instrument musical
• 
  El pedal està unit al canell per coixinets seguint una connexió de pivot
• 
  5 punts = pivot

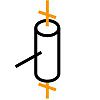
Pivot d'eix (A,Z)				Unions : Tx = 0 Ty = 0 Tz = 0 Rx = 0 Ry = 0	Llibertat : Rz

Tot i això, és possible obtenir una connexió pivotant mitjançant un simple contacte, dos cons complementaris o dues superfícies de revolució de secció reduïda. Aquesta connexió es considera composta perquè les superfícies considerades aquí no tenen la forma totalment banal del cilindre simple.

Quan dos sòlids estan units pivotantment, hi ha almenys 2 punts fixos coincidents a cada sòlid. La recta que passa per aquests punts és l'eix de la unió.

Unió pivotant lliscant o cilindre/cilindre

La unió pivotant lliscant modela un contacte cilíndric de revolució.

S'obté quan tots els punts de contacte pertanyen a un o més cilindres coaxials. Totes les normals de contacte coincideixen amb l'eix d'aquests cilindres, que es converteix naturalment en l'eix de la connexió. Aquesta és l'única direcció característica.

Les caixes de canvi del 2CV i del 4L estan unides al tauler de control per un pivot lliscant.

Aquesta baula es comporta com dues baules lineals anulars. Té 4 graus de llibertat, ja que uneix les dues translacions i les dues rotacions transversals. Els graus de llibertat són la translació i la rotació axial.

Si la rotació pot tenir fàcilment una amplitud infinita (almenys una revolució), la translació es limita a les dimensions de les peces. Tot i això, en el domini operatiu observat, el modelatge es manté.

La definició completa d'aquest enllaç ha d'especificar la posició de l'eix. Com que és una línia recta, només és completa si s'especifiquen 2 punts que li pertanyen, o un punt i una adreça. Aquesta adreça és també l'única que es destaca.

• 
  Solució per a un pivot lliscant.
• 
  Les files de jugadors en miniatures d'un futbolí estan unides a la taula per un pivot lliscant.
• 
  4 punts = pivot lliscant

Pivot lliscant d'aeix (A,x)				Unions : Ty = 0 Tz = 0 Ry = 0 Rz = 0	Llibertat : Tx Rx

A diferència de la connexió anular lineal, aquesta requereix un centrat llarg. La distinció tecnològica entre ambdues es basa en la relació entre el radi i la longitud de va (assemblatge cilíndric):

• si L < R, s'acceptarà el model anul·lar. La folgança permet una gran desviació angular;
• si L > 2R, es requereix el model de pivot lliscant. El mateix joc radial fa menyspreable la desviació angular;
• entre tots dos, correspon al mecànic fer una elecció, que estarà motivada pels resultats esperats. En el cas d‟un estudi estàtic, es prefereix el model menys restrictiu i amb menys incògnites. En el cas d'un estudi cinemàtic, es prefereix la baula més restrictiva, que proporciona més equacions per resoldre el problema.

Aquesta baula és molt comuna en mecanismes, on de vegades es confon amb el baula lliscant. Tot i això, és menys restrictiu de crear. Alguns exemples són la connexió entre pistó i camisa, i, encara en el motor d'explosió, entre pistó i biela (encara que, també en aquest cas, pugui semblar una connexió pivotant). En tots dos casos, l'elecció d'una connexió menys constreta permet posicionar les peces de manera natural.

Connexió helicoïdal

Article principal: Barra roscada

Lliscament d'un eix estriat es modela mitjançant una connexió lliscant. Si enrotllem les estries al voltant de l'eix, ens trobem en presència d'un cargol a la seva femella. Això es coneix com a connexió helicoïdal.

El que caracteritza aquesta connexió és l'existència d'un moviment "combinat": la rotació és simultània a la translació en una relació anomenada pas de cargol, hèlix o rosca. Es tracta, per tant, d'un únic grau de llibertat.

La connexió té, per tant, 5 graus de connexió, incloent-hi 2 translacions i 2 rotacions transversals. L'altre és degut a l'acoblament de la translació axial i la rotació mitjançant una relació helicoïdal del tipus x = u-θx. El pas de l'enllaç p = 2π-u indica la longitud recorreguda en una revolució (2π radians).

La definició d'aquest enllaç ha d'especificar la posició del seu eix, la direcció de l'hèlix i el valor del pas.

La consideració d'aquesta connexió és essencial en l'estudi dels dispositius de cargol-femella, la finalitat de la qual és transformar el moviment de rotació en moviment de translació. En canvi, l'estudi d'un conjunt que utilitzi perns o cargols no requereix aquesta modelització. Hi ha clavegueres a boles (associats a la rosca) dissenyats per transmetre el moviment, i que ofereixen una excel·lent eficàcia.

La direcció de l'hèlix, sovint cap a la dreta, es pot invertir. L'antic esquema (encara vàlid) proposat aquí permet (a diferència del nou) distingir entre tots dos casos.

• 
  Un cargol i diverses femelles
• 
  La femella i la claveguera de boles són, per a l'helicoïdal, l'equivalent del rodament.
• 
  5 punts = helicoïdal
• 
  Peces de connexió per cargol i femella.

Helicoidal a l'eix (A,X) i de pas p				Unions : x = u·θx Ty = 0 Tz = 0 Ry = 0 Rz = 0	Llibertat : ${\begin{pmatrix}u.\theta _{x}\\0\\0\\\theta _{x}\\0\\0\end{pmatrix}}$

Connexió cilindre/pla

Aquesta connexió s'obté quan presenta un conjunt de punts de contacte alineats les normals dels quals estan totes en el mateix pla. L'ideal és l'associació de 2 punts.

Hi ha 2 graus de connexió: la translació perpendicular al pla tangent (és a dir, a la direcció de les normals) i qualsevol rotació amb un eix perpendicular al pla de les normals de contacte.

Tot i la seva simplicitat, aquesta connexió és sens dubte la més tridimensional de totes, ja que el seu comportament és diferent de les 3 direccions de l'espai. Per tant, la vostra definició completa ha d'especificar el pla que conté l'adreça de la línia de punts de contacte i l'adreça comuna de les normals de contacte.

Com en el cas del contacte puntual, el contacte al llarg d'una línia (de gruix nul) és improbable. Es produeix deformació sota pressió. Una superfície rectangular de poca amplada es pot considerar una línia de contacte: un corró sobre el seu suport o una placa col·locada sobre una vora prima són casos de contacte lineal rectilini.

També en aquest cas, el resultat acostuma a ser una connexió unilateral real. No obstant això, un passador ajustat que llisca en una ranura oblonga és una solució bilateral. Les dues línies de contacte són paral·leles i es troben en un pla que també conté el conjunt de normals de contacte.

• 
  Connexió lineal rectilínia per cilindre col·locat en un pla
• 
  2 punts = rectilínia
• 
  En un engranatge recte, l'enllaç entre dues rodes es pot modelitzar mitjançant un rectilini lineal si el gruix dels pinyons no és menyspreable.
• 
  Solució bilateral.

Lineal rectilínia d'ei (A,x) i de normal Z				Unions : Tz = Z Ry = M	Llibertat : Tx, Ty Rx, Rz

Quan dues parts estan unides per una línia recta, hi ha dos punts fixos duna de les parts que coincideixen amb una superfície fixa de l'altra.

Bibliografia

• Feynman, Richard (1999). Lectures on Physics. Perseus Publishing. ISBN 978-0-7382-0092-7.
• Landau, L. D.; Lifshitz, E. M. (1972). Mechanics Course of Theoretical Physics , Vol. 1. Franklin Book Company. ISBN 978-0-08-016739-8.
• Eisberg, Robert Martin (1961). Fundamentals of Modern Physics. John Wiley and Sons.

Vegeu també

• Mecanisme
• Graus de llibertat (enginyeria)
• Articulació (mecànica)