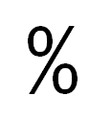Percentatge
Un percentatge és una forma d'expressar una proporció o fracció com a fracció de denominador 100, és a dir, com a quantitat de centèsimes.[1] L'expressió «45 %» («45 per cent») és el mateix que la fracció 45/100 o que el nombre decimal 0,45.
Per exemple, una fracció 2/5, expressat en un percentatge seria convertir a decimal 0,4 multiplica 0,4 per 100 per convertir a percentatge. 0,4 ⋅ 100 simplifica 0,4 ⋅ 100 . 40 %
Un percentatge pot ser major de 100. Per exemple, el 200 % d'un nombre és el doble del mateix nombre, o un increment del 100 %. Un increment del 200 % en canvi donaria com a resultat el triple de la quantitat inicial, moment en què ens adonem de la diferència de la relació existent entre augment percentual i del producte.
Els percentatges s'utilitzen per expressar com de gran o de petita és una quantitat comparant-la amb una altra quantitat. Normalment la primera quantitat representa una part de, o un canvi de la segona quantitat que ha de ser major que zero. Per exemple un increment de 0,15 $ en un preu de 2,50 $ és un increment de la fracció de 0,15 / 2,50 = 0,06. Expressat com a percentatge és un increment d'un 6 %. Malgrat que els percentatges que s'utilitzen habitualment són nombres entre zero i u, no tenen dimensió. La proporcionalitat es pot expressar com un percentatge. Per exemple, 111 % és 1,11 i -0,35 % és -0,0035.
-
Anotació del percentatge al s.XVIII.
-
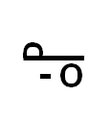
Anotació del percentatge al s.XVII.
-
Anotació del percentatge al s.XV.
Exemples
[modifica]- «El 45 % de la població humana...» és equivalent a «45 de cada 100 persones...».
- «200 % d'un nombre» és equivalent al «doble del mateix nombre» que alhora és el mateix que «un increment del 100 % del nombre».
Història
[modifica]En l'Antiga Roma, molt abans de l'existència del sistema decimal, se solien fer càlculs en fraccions de múltiples de 1100. Per exemple, August va crear un impost de 1100 en béns venguts en subhastes coneguda com centesima rerum venalium. El càlcul amb aquestes fraccions era equivalent al càlcul amb tants per cent.
A mesura que van créixer les denominacions dels diners en l'edat mitjana, el càlculs amb denominador de 100 es van anar estandarditzant, de tal manera que a finals del segle xv i a principis del XVI, era habitual trobar tals càlculs en llibres d'aritmètica. Molts d'aquests llibres aplicaven aquests mètodes per guanys i pèrudes, taxes d'interès i per a la regla de tres. Ja al segle xvii, era estàndard referir-se a les taxes d'interès per centèsimes parts.[2]
El símbol
[modifica]El símbol «%» és una forma estilitzada dels dos zeros. Aquest va evolucionar a partir d'un símbol similar només que es representava per una línia horitzontal en comptes de la diagonal (any 1650) que alhora provenia d'un símbol representat per P cento (any 1425).
El terme "per cent" deriva del llatí per centum, que significa "cent" o "per cent".[3][4] El signe de "per cent" va evolucionar a partir de la contracció gradual del terme italià per cento, que signfica "per cent". El "per" solia abreviar-se com "p."—fins al punt que va desaparèixer completament. El "cento" es va contraure a dos cercles separats per una línia horitzontal, d'on deriva el símbol modern "%".[5]
Proporció
[modifica]Els percentatges s'utilitzen per expressar parts del total. Per exemple, 25 % significa 25 / 100, o una quarta part, d'un determinat total. Existeixen els percentatges majors (com per exemple «una família ha de guanyar com a mínim 125 % per sobre de la línia de la pobresa per tenir una visa»).
Càlculs
[modifica]El concepte fonamental a recordar quan es fan càlculs amb percentatges és que el símbol de tant per cent es pot tractar com la constant ., per exemple el 35 % de 300 es pot escriure com (35 / 100) × 300 = 105. Per trobar el tant per cent d'una unitat en un conjunt total de N unitats cal dividir 100 % per N. Per exemple, si es tenen 1250 pomes i es vol trobar quin percentatge d'aquestes 1250 pomes representa una única poma, 100 % / 1.250 = (100 / 1250) % que dona 0,08 %. Per calcular el percentatge d'un altre percentatge, s'han de convertir tots dos a fraccions de 100 o a nombres decimals i multiplicar-los. Per exemple, el 50 % de 40 % és: (50 / 100) × (40 / 100) = 0,50 × 0,40 = 0,20 = 20 / 100 = 20 %. No és correcte dividir per 100 i utilitzar el signe de tant per cent al mateix temps. (E.g. 25 % = 25 / 100 = 0.25, no pas 25 % / 100, sinó (25 / 100) / 100 = 0,0025.)
Problemes d'exemple
[modifica]Quan es parla de percentatges, és important especificar a què ens estem referint, és a dir quin és el total que es correspon al 100 %. El següent problema il·lustra aquest fet: en un determinat col·legi el 60 % del total d'estudiants són noies i el 10 % de tots els estudiants són estudiants d'informàtica. Si el 5 % de les noies són estudiants d'informàtica, quin percentatge d'estudiants d'informàtica són noies? Es demana calcular la raó entre el nombre d'estudiants noies d'informàtica i el nombre total d'estudiants d'informàtica. Se sap que el 60 % del total d'estudiants són noies, i entre aquestes el 5 % són estudiants d'informàtica, per tant es pot concloure que (60 / 100) × (5/100) = 3/100 o 3 % de totes les noies estudiants d'informàtica. Dividint-ho pel 10 % de tots els estudiants d'informàtica s'arriba a la resposta: 3 % / 10 % = 30 / 100 o 30 % són noies. Aquest exemple està molt relacionat amb el concepte de probabilitat condicionada.
D'altres exemples:
- Quin és el 200 % de 30?
- Resposta: 200 % × 30 = (200 / 100) × 30 = 60.
- Quin és el 13 % de 98?
- Resposta: 13 % × 98 = (13 / 100) × 98 = 12,74.
- 60 % de tots els estudiants universitaris són homes. Hi ha 2400 estudiants homes. Quants estudiants hi ha a la universitat?
- Resposta: 2.400 = 60 % × X, per tant X = (2.400 / (60 / 100)) = 4.000.
- Al poble del costat hi ha 300 gats i 75 són negres. Quin tant per cent de gats negres hi ha al poble?
- Resposta: 75 = X % × 300 = (X / 100) × 300, per tant X = (75 / 300) × 100 = 25, i llavors X % = 25 %.
- El nombre d'estudiants a la universitat ha pujat de 4125 que hi havia el curs passat a 4620, un increment de 495 estudiants. Quin és l'increment percentual?
- Resposta: 495 = X % × 4.125 = (X / 100) × 4.125, per tant X = (495 / 4.125) × 100 = 12, i llavors X % = 12 %.
Altres usos
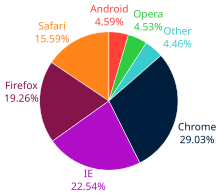
[modifica]Termes utilitzats en els mitjans de comunicació així com en l'àmbit esportiu com 'Els jugadors han donat aquesta nit el 110 % en el terreny de joc' no tenen cap sentit en l'àmbit de les matemàtiques. Sovint s'utilitza erròniament la paraula «percentatge» en l'àmbit de les estadístiques esportives, quan el nombre al qual es refereix s'expressa com una proporció decimal i no com un percentatge: «El Phoenix Suns Shaquille O'Neal anava primer de l'NBA amb un percentatge d'efectivitat de .609 durant la temporada 2008-09.» (O'Neal va ficar el 60,9 % dels seus llançaments, no 0,609 %). Probablement la pràctica està relacionada de manera similar que es veu en les estadístiques dels batejadors. També s'utilitza el percentatge per a descriure el pendent d'una carretera que puja o baixa. Els signes percentuals també es poden utilitzar per fer que alguna cosa sembli més oficial i creïble.
Percentatges per incrementar i disminuir
[modifica]Algunes vegades a causa d'un ús erroni, no queda clar a partir del context a què es refereix el percentatge. Quan es parla d'una «pujada del 10 %» o una «baixada del 10 %» d'una quantitat, la interpretació usual és que es refereix al valor inicial d'aquesta quantitat. Per exemple, si un objecte tenia un preu inicial de 200 $ i el preu puja un 10 % (un increment de 20 $), el nou preu serà 220 $. Cal notar que el preu final és un 110 % del preu inicial (100 % + 10 % = 110 %).
D'altres exemples de canvis percentuals:
- un increment de 100 % en una quantitat significa que la quantitat final és el 200 % de la quantitat inicial (100 % de l'inicial + 100 % de l'inicial = 200 % de l'inicial); dit d'una altra manera, la quantitat s'ha doblat.
- un increment del 800 % significa que la quantitat final és 9 vegades l'original (100 % + 800 % = 900 % = 9 vegades més gran).
- Una rebaixa del 60 % significa que la quantitat final és el 40 % de l'original (100 % − 60 % = 40 %).
- Una rebaixa del 100 % significa que la quantitat final és zero (100 % − 100 % = 0 %). En general, un canvi de per cent en una quantitat resulta que la quantitat final és per cent de la quantitat inicial (equivalentment, vegades la quantitat inicial). És important entendre que canvis en el percentatge, tal com ha estat discutit aquí, no afegeix de la manera habitual, si s'apliquen seqüencialment. Per exemple, si el 10 % d'increment en el preu que s'ha parlat anteriorment (en l'objecte de $200, apujava el seu preu a $220) és seguit d'una rebaixa del 10 % en el preu (una rebaixa de $22), el preu final serà $198, no el preu inicial de $200. La raó per l'aparent discrepància és que els dos canvis percentuals (+10 % i−10 %) es mesuren relativament a quantitats diferents ($200 i $220, respectivament), i per tant no es "cancel·len". En general, si un increment percentual de és seguit per una rebaixa de per cent, i la quantitat inicial era , la quantitat final serà ja que el canvi és una disminució global de per cent de per cent (el quadrat del canvi percentual original quan s'expressa com a nombre decimal). Per tant, en l'exemple anterior, després d'un increment i una rebaixa de per cent, la quantitat final $198 era el 10 % del 10 %, o 1 %, menys que la quantitat inicial de $200. Això es pot generalitzar pel cas en el qual no es té el mateix percentatge de canvi. Si el percentatge inicial de canvi és i la segona quantitat és , i la quantitat inicial era , llavors la quantitat final és . Per aplicar l'exemple anterior, després d'un increment de i una rebaixa de per cent, la quantitat final és $209, que és 4,5 % més que $200. En el cas de taxes d'interès, és una pràctica habitual posar el canvi percentual d'una altra manera. Si una taxa d'interès puja de 10 % a 15 %, per exemple, és típic dir, «La taxa d'interès s'ha incrementat un 5 %» — en lloc d'un 50 %, que és el que seria correcte quan es mesura com a percentatge de la taxa inicial (i.e., de 0,10 a 0,15 hi ha un increment de 50 %). Aquesta ambigüitat es pot evitar utilitzant el terme «punts percentuals». En l'exemple anterior, la taxa d'interès s'ha «incrementat en 5 punts percentuals de 10 % a 15 %». Si la taxa baixa 5 punts percentuals, tornarà a la taxa inicial del 10 %, com era d'esperar.
- L'any 2012 el Gobierno espanyol decidí augmentar l'IVA d'alguns productes com la plastilina o els quaderns escolars. Abans estaven gravats amb el tipus superreduït (4 %) i han passat a estar gravats amb el general (21 %).[6] S'acostuma a dir equivocadament «L'increment ha estat del 17 % (21 %-4 %=17)». Aquest increment però, si es calcula bé, ha estat del 425 %: (21 - 4) / 4 × 100) = 425 %. Sí que es tractaria, doncs, d'un augment de 17 punts percentuals.
Errors més habituals
Sumar o restar directament %
Un dels errors més comuns que es fa, és atorgar als percentatges un valor numèric fix i després sumar o restar-los directament. En algun mitjà de comunicació he vist «l'IVA de la benzina, a Espanya, a partir de l'1 de setembre s'incrementà un 3 %, passarà del 18 % al 21 %». Si ho calculem ens adonarem que s'ha incrementat ni més ni menys que un 16,67 % molt per sobre del que indicava el periòdic.
La forma correcta de la notícia hagués estat «l'IVA de la benzina, a Espanya, a partir de l'1 de setembre s'incrementà 3 punts, passarà del 18 % al 21 %».
Acumular directament %
Sovint trobem qui conclou que, si un mes la benzina puja el 5 % i al mes següent un altre 5 %, l'augment de la benzina dels dos mesos ha estat del 10 %, quan en realitat l'augment ha estat del 10,25 %.
Un altre error el trobem quan algú conclou que si un mes la borsa (IBEX) puja el 20 % i al més següent baixa un 20 % queda invariant. Si fem els càlculs correctament ens adonarem que si que ha variat, ja que en realitat ha baixat un 4 %.
Els percentatges tenen un comportament diferent al fet pujar i baixar escales (si pugem 20 escales i després en baixem 20 tornarem al punt de partida).
I ens podem preguntar, a què es deuen aquests errors? Això passa per no considerar que el percentatge és una relació de proporcionalitat respecte a valors diferents. El mateix % a l'aplicar-lo a quantitats diferents dona valors diferents.
Vegem un exemple. Si l'IBEX puja un 20 % al gener i un 20 % al febrer, quina ha estat la pujada dels dos primers mesos de l'any?
| Valor a principi d'any (1G) | Valor a 31G | Valor a 28F |
| x | x+(20/100)x=1,2x | 1,2x+(20/19991,2x=1,44x |
Hem passat d'un valor «x» a un valor 1,44x i això representa un increment del 44 %.
I un es podria preguntar, hi ha alguna manera més senzilla d'encadenar %?. Doncs SÍ.
Si analitzem la següent taula d'encadenament de percentatges
| Primer % | Segon % | % Global |
| 20 | 20 | 44 |
| 30 | 80 | 134 |
| 80 | 30 | 134 |
| 50 | -30 | 5 |
| 10 | -40 | -34 |
| -70 | 10 | -67 |
| -10 | -20 | -28 |
| A | B | C |
podem deduir que C=A+B+(A/10)·(B/10). És a dir, el percentatge acumulat és igual a la suma de percentatges més el producte de les desenes d'aquests (tenint en compte els signes corresponents). Comproveu-ho.
Referències
[modifica]- ↑ «Percentatge». Gran Enciclopèdia Catalana. [Consulta: 15 agost 2022].
- ↑ Smith, 1958, p. 247-249.
- ↑ Houghton Mifflin. American Heritage Dictionary of the English Language (en anglès). 3a, 1992.
- ↑ «Definition of PERCENT» (en anglès). [Consulta: 28 agost 2020].
- ↑ Smith, D.E.. History of Mathematics. 2. Courier Dover Publications, 1958, p. 250. ISBN 0-486-20430-8.
- ↑ «El material escolar tributarà el 21 % d'IVA al setembre». El Punt Avui, 07-08-2012 [Consulta: 21 gener 2015].
Bibliografia
[modifica]- Smith, D.E.. History of Mathematics (en anglès). 2. Courier Dover Publications, 1958. ISBN 0-486-20430-8.
Vegeu també
[modifica]Enllaços externs
[modifica]- «Percent change calculator» (en anglès). percent-change.com.
- «Express learning - percentages / BBC raw money» (en anglès). BBC. Arxivat de l'original el 2010-01-20. [Consulta: 26 març 2021].
- «Percentage Calculator» (en anglès).
- «Percent off calculator» (en anglès).