Zona de càrrega espacial

En electrònica, la zona d'esgotament, també anomenada zona de càrrega espacial (ZCE), o zona deserta, correspon a la regió que apareix en una unió PN, entre la zona dopada N i la zona dopada P. S'anomena "zona d'esgotament" o "zona de depleció" perquè no té portadors lliures, i s'anomena "zona de càrrega espacial" perquè consta de dues àrees de càrrega elèctrica (a diferència de la resta dels semiconductors N i semiconductors P que són globalment neutres) ...

Formació

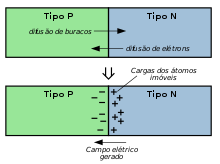
Quan es posa en contacte un tipus semiconductor amb un semiconductor de tipus P (unió PN), els electrons predominen al costat N (respectivament els forats majoritaris del costat P). seran arrossegats cap a la zona P (respectivament cap a la zona N pels forats) on siguin minoritàries, per fenomen de difusió. En fer-ho, deixen enrere ions de les càrregues oposades, cosa que va assegurar la neutralitat elèctrica dels semiconductors N i P abans que es posessin en contacte. Finalment, els electrons (o forats) que s'han desplaçat a la zona P es recombinen amb els forats majoritaris (respectivament amb la majoria d'electrons a la zona N).^[1]

Per tant, hi ha una aparició en el semiconductor tipus N d'una zona lliure d'electrons a la unió (respectivament, una zona sense forats del semiconductor tipus P), mentre que aquesta zona sempre conté els ions resultants. àtoms de dopatge. Aquells ions la càrrega total Q> 0 (Q <0 a la zona P) deixa de ser compensada per electrons creen un camp elèctric que es pot calcular integrant la equació de Poisson.^[2] La juxtaposició d'aquestes dues zones privades de transportadors lliures i carregades elèctricament constitueix la zona d'esgotament

El camp elèctric generat per aquesta zona, orientat en la direcció de les càrregues positives (a la zona N) cap a les càrregues negatives (a la zona P), fa que els electrons i els forats en sentit contrari al fenomen de difusió. Així la unió arriba a un equilibri perquè el fenomen de difusió i el camp elèctric es compensen mútuament.

Referències

↑ Olivier Bonnaud, Components semiconductors: de la física d'estats sòlids als transistors, ed. Ellipses, Plantilla:Coll., 2006, 241 Plantilla:Nb p. ISBN 978-2-7298-2804-2, p. 90-91.
↑ Olivier Bonnaud, Components semiconductors, Plantilla:Opcit, p. 93.

Vegeu també

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Zona de càrrega espacial

[1] Olivier Bonnaud, Components semiconductors: de la física d'estats sòlids als transistors, ed. Ellipses, Plantilla:Coll., 2006, 241 Plantilla:Nb p. ISBN 978-2-7298-2804-2, p. 90-91.

[2] Olivier Bonnaud, Components semiconductors, Plantilla:Opcit, p. 93.

[1]

[2]