Usuari:Mcapdevila/Moment flector

Biga simplement recolzada, sol·licitada a flexió per sobrecàrrega uniformement distribuïda.

El moment flector és un moment de força resultant d'una distribució de tensions sobre una secció transversal d'un prisma mecànic flexionat o una placa que és perpendicular a l'eix longitudinal al llarg del qual es produeix la flexió. És una sol·licitació típica en bigues i pilar és i també en lloses, ja que tots aquests elements solen deformar-predominantment per flexió. El moment flector pot aparèixer quan es sotmeten aquests elements a l'acció un moment (torque) o també de forces puntuals o distribuïdes.

Diagrama de moment flector

Flexió d'una biga simplement recolzada.

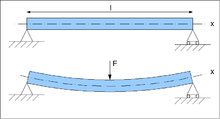
Per elements lineals perpendiculars tipus barra, el moment flector es defineix com una funció al llarg de l'eix neutre de l'element, on "x" representa la longitud al llarg d'aquest eix. El moment flector així definit, donades les condicions d'equilibri, coincideix amb la resultant de forces de totes les forces situades a un dels dos costats de la secció en equilibri en la qual pretenem calcular el moment flector. Com que un element pot estar subjecte a diverses forces, càrregues distribuïdes i moments, el diagrama de moment flector varia al llarg del mateix. Així mateix les càrregues estaran completades en seccions i dividides per trams de seccions. En una peça de pla mitjà, si es coneix el desplaçament vertical de l'eix baricéntric sobre aquest pla el moment flector pot calcular a partir de l'equació de la corba elàstica:

$M_{f}(x)={\frac {d}{dx}}\left(EI_{f}{\frac {di}{dx}}\right)$

On:

$I(x)\,$ és el desplaçament vertical o desplaçament de la corba elàstica.

$I\,$ és el mòdul de Young del material de la biga.

$I_{f}\,$ és el segon moment d'àrea de la secció transversal de la biga.

A més el moment flector sobre una biga de pla mitjà ve relacionat amb l'esforç tallant per la relació:

${\frac {dM_{f}(x)}{dx}}=-V(x)$

Mètode de les seccions

El primer mètode que s'usa per a la construcció de diagrames de moments és el mètode de seccions, que consisteix a realitzar talls imaginaris al llarg d'un element i aplicar les equacions de l'equilibri. Suposem que es realitza un tall imaginari sobre una biga, com la peça continua al seu lloc, es pot considerar que es troba encastat a l'altra part de la biga, de manera que hi ha reaccions que impedeixen el desplaçament. En el cas del moment, és possible realitzar una suma de moments en el punt en què es va realitzar el "tall". S'ha de comptar cada força, càrrega distribuïda i moment fins on es va realitzar el tall. En el mètode de seccions és necessari realitzar un tall per cada factor que canviï la distribució del diagrama de moments.

Mètode dels trams

Un altre mètode utilitzat per a la construcció de diagrames de moments són les funcions discontínues, que serveix per construir una funció contínua a trams. En el cas que un element estigués sotmès a diverses forces, càrregues i moments la quantitat de talls que serien necessaris torna al procediment tediós i repetitiu. Si s'observa amb cura, l'equació de moment augmenta un terme per cada tall que es realitza a causa de la nova força, càrrega distribuïda o moment que s'agrega. L'ús de les funcions discontínues consisteix a agregar funcions que "s'activin" quan s'arriba a certa posició (on abans es posava el tall). Aquestes funcions es defineixen de la manera següent:

$<x-a>^{n}={\begin{cases}0,&{\mbox{si }}x<a\\<x-a>^{n},&{\mbox{si }}x\geq a\end{cases}}$

Mètode de la integració directa

Una altra possibilitat és usar fórmules vectorials directes, si es tenen forces puntuals i reaccions verticals $p_{1},...,p_{n}\;$ aplicades en els punts $x_{1}<...<X_{n}\;$, una càrrega distribuïda contínua $q(x)$ i moments puntuals $M_{1},...,M_{m}\;$ situats a la dreta de la secció, el moment flector total pot calcular directament com:

$M_{f}(x)=(M_{1}+...+M_{m})+\sum _{i=1}^{k}P_{i}(x-x_{i})+\int _{0}^{x}ds\int _{0}^{s}q({\bar {s}})\ d{\bar {s}}$

On la suma sobre i s'estén fins k donat per la condició $x_{k}\leq x$. L'anterior funció serà contínua si i només si tots els moments puntuals es len, i serà diferenciable si només hi ha càrrega contínua q. Quan les forces puntuals no siguin totes nul la funció serà contínua a trams.

Càlcul de tensions en flexió

En un element constructiu prismàtic sotmès a flexió es generen tensions normals a la secció transversal, $\sigma$, de sentit oposat a la zona comprimida i en la zona traccionada, que generen un moment resultant de les tensions internes que iguala el moment exterior aplicat.

Flexió simple no desviada

Quan una peça prismàtica està sent flectades per un moment flector que coincideix vectorialment en direcció amb un dels eixos principals d'inèrcia es diu que està sotmès a flexió no desviada, si a més no hi ha esforç axial la flexió es diu simple, i si a més la secció té un pla de simetria perpendicular al moment, situació que succeeix típicament en les estructures convencionals, la tensió normal en qualsevol punt es produeix en una biga o un element flectades en aplicar un moment flector es pot aproximar per la fórmula de Navier:

$\sigma (x,y)=-{\frac {M_{f}(x)y}{I_{f}}}$

On M _f és el moment aplicat, i és la distància des del baricentre (centre de gravetat de la secció) a la fibra considerada, i I _f és el segon moment d'inèrcia de la secció respecte a l'eix de flexió. Per a més practicitat, sol utilitzar-se el moment resistent, calculat com:

$W_{c}={\frac {I_{f}}{y_{c}}}$

On $y_{c}$ és la distància màxima del baricentre al cordó superior o al cordó inferior, segons es vulgui calcular compressions o traccions màximes.

Per peces simètriques respecte del baricentre, carregades només amb forces contingudes en el pla de simetria que passa pel baricentre, el càlcul de la tensió màxima en valor absolut es redueix al càlcul del quocient:

$\sigma _{max}={\frac {M_{f}}{W_{min}}}$

Flexió desviada i flexo-torsió

Per peces no simètriques o amb flexió desviada, la situació és més complicada. En peces no simètriques per exemple el centre de tallant usualment no coincideix amb el centre de gravetat la qual cosa provoca acoblament entre flexió i torsió, la qual cosa vol dir que si hi ha flexió existirá simultàniament torsió i viceversa, la qual cosa obliga a computar el moment torsor i les tensions tangencials per a poder estimar la tensió màxima.

En el cas de peces amb flexió desviada, és a dir, peces amb flexió segons una direcció que no coincideix amb els eixos principals d'inèrcia, la tensió pot estimar descomponent el moment flector segons els eixos principals d'inèrcia. Si a més el centre de tallant coincideix amb el centre de gravetat i la curvatura de la secció pot menysprear, podem estimar la tensió màxima com:

$\sigma _{max}={\frac {N_{x}}{A}}+{\frac {m_{f1}}{W_{1}}}+{\frac {m_{f2}}{W_{2}}}$

On:

$A,W_{1},W_{2}\;$, són l'àrea i els moments resistents de la secció.

$N_{x},m_{f1},m_{f2}\;$, són el esforç axial i les components del moment flector projectat sobre els dos eixos d'inèrcia perpendiculars.

Quan a més existeix torsió no és menyspreable el guerxament, ni sent els eixos de referència necessàriament eixos principals l'expressió de la tensió en qualsevol punt genèric ve donada per:

$\sigma (x,y,z)={\frac {N_{x}(x)}{A}}+{\frac {zI_{z}-yI_{zy}}{I_{y}I_{z}-I_{yz}^{2}}}M_{y}(x)+{\frac {yI_{y}-zI_{yz}}{I_{y}I_{z}-I_{zy}^{2}}}M_{z}(x)+\omega {\frac {B_{\omega }(x)}{I_{\omega }}}$

On:

$I_{z},I_{y},I_{yz}\;$, són els moments d'àrea de la secció.

$I_{\omega }\;$, és el moment de guerxament.

$M_{y},M_{z},B_{\omega }\;$, són les components del moment flector sobre els eixos arbitraris i el bimoment associat a la torsió.

Vegeu també

• Esforç intern

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Mcapdevila/Moment flector