Altímetre

Un altímetre és un instrument de mesura que indica la diferència d'altitud entre el punt on es troba localitzat i un punt de referència; habitualment s'utilitza per conèixer l'altitud sobre el nivell del mar d'un punt.^[1]

Els altímetres són aparells bàsics en avions, ultralleugers, globus aerostàtics... En esports o activitats en què es pateixen grans desnivells, com el muntanyisme, ciclisme, esquí, escalada, paracaigudisme, etc., S'utilitza per conèixer els desnivells que s'estan superant. També s'empren en estudis duts a terme per satèl·lits artificials sobre la superfície de la Terra, i per sondes espacials sobre les superficies d'altres planetes i llunes.N'hi ha de tres tipus: baromètrics, de radar i làser.

Altímetre baromètric

Història

L'altímetre baromètric és l'aparell més comú de tots els tipus d'altímetres i el més antic. Fou inventat cap al 1880 pel físic francès Louis-Paul Cailletet (1832-1913) malgrat que els pioners en les ascensions aerostàtiques empraren baròmetres, a partir de les mesures dels quals calculaven les altures assolides. Aquests altímetres, amb càpsules baromètriques calibrades a nivell del mar, començaren a utilitzar-se en aviació des d'aproximadament 1913.^[2] Tanmateix, les lectures d'aquests primers altímetres no eren del tot precises, ja que no tenien possibilitat de fer correccions quan hi havia canvis en la pressió de referència a nivell de la mar. Fou per això que, el 1929, l'enginyer alemany Paul Kollsman (1900-1982) introduí algunes modificacions per a millorar significativament la precisió. El pioner en aviació estatunidenc Jimmy Doolittle (1896-1993) encarregà a Kollsman, que havia emigrat als Estats Units, un altímetre baromètric que fos molt més precís que els existents i que permetés ajustar-lo a les condicions de pressió reals que existissin a l'atmosfera. El 24 de setembre de 1929 es dugué a terme el primer vol completament instrumental, realitzat per Doolittle, que portava a bord el primer altímetre regulable en pressió. A partir de llavors, i atès l'èxit de la prova, els altímetres començaren a incorporar la famosa “finestreta de Kollsman” on es pot introduir el reglatge altimètric.^[2]

Fonament

El seu funcionament està basat en la relació entre pressió i altitud, car la pressió atmosfèrica baixa amb l'altitud (uns 10 kPa els primers 3 000 m d'altitud, després més lentament). Es pren com a base de referència el nivell del mar, però el seu funcionament està condicionat als canvis meteorològics, de manera que un altímetre de certa qualitat ha de permetre compensar les variacions de pressió provocades, per exemple, quan es passa amb un avió d'una zona de baixes pressions a una d'altes. Aquests altímetres tenen un funcionament irregular si el canvi d'altitud és molt brusc, ja que triguen a respondre i captar la pressió atmosfèrica; tampoc funcionen bé si, per exemple, es realitza l'ascensió en un cotxe amb les finestres tancades, ja que en l'interior del cotxe amb les finestres tancades la pressió serà molt diferent de la de l'exterior. Per altra banda, l'altímetre mesura l'altitud, això és, l'alçada des del nivell de la mar i no l'altura sobre el terreny.^[3]

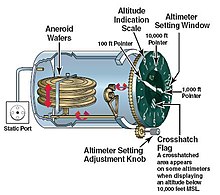
El funcionament de l'altímetre està basat en els canvis de volum que experimenta una càpsula aneroide, igual que la dels baròmetres aneroides. La càpsula aneroide és una càpsula metàl·lica de parets molt primes, a l'interior de la qual s'ha fet un buit parcial, de tal manera que les variacions de la pressió atmosfèrica deformen les seves parets.^[4] Aquestes deformacions són mesurades mitjançant un mecanisme que les tradueix en mesures d'altitud, pel que fa a una pressió que s'ha reglat mitjançant el sistema de reglatge que s'usa per corregir la mesura d'altitud pels canvis de pressió atmosfèrica (pressió de referència), aquesta dada de reglatge s'obté d'un baròmetre instal·lat al punt respecte del qual es vol fer el mesurament.^[3]

La pressió atmosfèrica disminueix amb l'altitud pel fet que la massa d'aire també ho fa. És per la mateixa raó que la pressió hidroestàtica augmenta amb la profunditat, ja que la massa d'aigua que hi ha damunt el punt també augmenta. S'ha determinat que la pressió atmosfèrica varia amb l'altura segons l'equació baromètrica:^[5]

$P_{z}={\frac {P_{0}}{e^{\tfrac {z}{H}}}}$ on:

$z$ és l'altitud.

$P_{z}$ és la pressió atmosfèrica a l'altitud $z$ .
$P_{0}$ és la pressió atmosfèrica estàndard a nivell de la mar, 101 325 Pa.
$H={\tfrac {kT}{mg}}=29,55T$ $H={\tfrac {kT}{mg}}=29,55T$ , on:
- $k$ és la constant de Boltzmann, 1,38 × 10^–23 m² kg s^–2 K^–1
- $T$ és la temperatura mitjana, en kèlvins, entre el valor a la superfície de la Terra i l'altitud $z$ .
- $m$ és la massa mitjana de les molècules d'aire, 4,76 × 10^–26 kg.
- $g$ és l'acceleració de la gravetat a la superfície terrestre, 9,81 m s^–2 (se suposa que la variació amb l'altitud és negligible)

Operant aquesta equació es pot posar l'altitud $z$ en funció de la pressió $P_{z}$ . S'obté l'anomenada equació hipsomètrica, on $z$ es dona en metres i les pressions en qualssevol unitats sempre que siguin les mateixes per a ambdues pressions:^[5]

$z=H\ln P_{0}-H\ln P_{z}=H\ln {\frac {P_{0}}{P_{z}}}$ Per tant, si hom mesura la pressió a una certa altitud, mitjançant l'equació hipsomètrica pot obtenir el valor d'aquesta altitud. Habitualment s'expressa com l'equació coneguda com a fórmula baromètrica internacional:

$z=44\,330-4\,935,\!125\,{P_{z}}^{0,\!1903}$

Funcionament

La busca curta i prima passa l'1, que significa que està per damunt els 10 000 peus. La busca curta i gruixada ha passat el 4, per tant, l'avió vola a més de 4 000 peus més que els 10 000. La busca llarga marca el 5, indicant 500 peus més. En resum, l'avió vola a 14 500 peus.

Un altímetre baromètric analògic dels avions o ultralleugers es llegeix de manera similar a la d'un rellotge, també analògic. Generalment, el dial està graduat amb nombres que van de 0 a 9 en el sentit de les agulles del rellotge, amb divisions intermèdies de 20 a 20 peus.^[3]

Si l'altímetre té dues busques, que és habitual en avions lleugers, la més curta indica milers de peus (1 peu = 0,305 m), i la més llarga centenes de peus. Una indicació en forma de finestra inferior ratllada és visible a altituds per sota de 10 000 peus i invisible per damunt aquesta altitud. Una volta sencera de la busca llarga suposa 1 000 peus i que la busca curta es mogui al número següent o anterior. Una volta completa de la busca curta suposa 10 000 peus i que s'oculti la finestra ratllada de la part inferior.^[3]

Si té tres busques, la tercera sol representar desenes de milers i hi ha dues possibilitats: que sigui més petita que les altres o que sigui molt més fina i amb un triangle a l'extrem. En el cas de la busca més petita, aquesta pugui quedar oculta per una de les més grans induint a un error de lectura pel que és més habitual la busca fina amb el triangle. Per a més seguretat, tots dos models solen disposar a més de la finestra ratllada que desapareix en superar els 10 000 peus.^[3]

L'altímetre presenta en unitats d'altitud els canvis de pressió de l'atmosfera real respecte a la pressió amb què estan calibrades les càpsules aneroides. Sota aquesta premissa, aquest instrument només mostraria l'alçada correcta si els valors atmosfèrics coincidissin amb els de l'atmosfera tipus. Però com és força improbable que les condicions reals coincideixin amb les estàndard, a més que aquestes condicions canvien contínuament i són diferents d'un lloc a l'altre, l'altímetre seria poc fiable i el vol es faria arriscat si no fos per la possibilitat d'ajustar-ho i compensar-ho per a situacions no estàndard. Aquest ajustament es fa mitjançant el botó d'ajust o reglatge altimètric, que permet seleccionar una pressió de referència que s'anirà mostrant a la finestreta de calibració a mesura que es gira el botó. Alguns models tenen una altra finestreta entre els números 7 i 8; una mostra pressions en polzades de mercuri i l'altra en mil·libars.^[3]

El moviment del botó d'ajust altimètric en realitat el que fa és dilatar o contraure les càpsules aneroides en les quals, d'acord amb la llei de Boyle-Mariotte “la pressió és inversament proporcional al volum”, canviarà el volum i amb això la pressió de referència, que quedarà ajustada a la seleccionada al dial. El moviment de les càpsules aneroides es reflecteix de forma simultània en la marcació de les agulles.^[3]

Altímetre de radar

Els altímetres de radar són més senzills i funcionen de manera similar al radar (el sistema que fan servir avions, vaixells i altres vehicles per navegar). Dit d’una altra manera, simplement emeten un feix d’ones de ràdio des d’un satèl·lit artificial o un avió cap al terra i esperen que les reflexions tornin. Com que les ones de ràdio viatgen a la velocitat de la llum (300 000 km/s), només triguen unes centèsimes de segon a fer el viatge d’anada i tornada d’uns 20 000 metres fins a la superfície terrestre. L’altímetre cronometra el feix i calcula la seva altitud en quilòmetres multiplicant el temps en segons per 150 000 (300 000 dividit per dos, ja que el feix ha recorregut dues vegades la seva altitud: d’anada al terra i de tornada). Els altímetres de ràdio són molt més ràpids i precisos que els altímetres baromètrics i s’utilitzen àmpliament en avions d’alta velocitat o en aquells que necessiten volar a altituds especialment baixes, com els avions de combat.^[6]

En general, la velocitat de la llum és aproximadament un milió de vegades més gran que la velocitat de creuer d’un avió típic (v), de manera que un senyal de ràdio reflectit al terra i tornat recorre una distància d’aproximadament el doble de l’altitud de l’avió. Per tant, l’altímetre ha de multiplicar el temps del senyal, que surt de l’emissor i es reflecteix al receptor, per la meitat de la velocitat de la llum. En teoria, com més ràpid viatja l’avió, menys precisa és la mesura, perquè el feix de ràdio ha de recórrer una distància més gran; però, en la pràctica, la velocitat de la llum és tan superior a la velocitat de l’avió que qualsevol error és mínim.^[6]

Els altímetres de radar també són importants per a la geologia. Aquests instruments han proporcionat una mesura de la forma del geoide en les conques oceàniques, que reflecteix els processos dinàmics de la tectònica de plaques: subducció i dorsals d’expansió.^[7] Els altímetres radar en òrbita terrestre s’han utilitzat principalment per mesurar les altures de la superfície del mar i per determinar paràmetres del geoide terrestre.^[8] Són exemples d'altímetres de radar els següents sensors: ALT (SeaSat), GRA (GEOSAT), NRA (TOPEX-Poseidon), Poseidon-1 (TOPEX-Poseidon), Poseidon-2 (Jason-1), Poseidon-3 (Jason-2), RA-1 (ERS-1 i ERS-2), RA-2 (Envisat), SIRAL (CryoSat), SRAL (Sentinel-3).^[9]

Aquests altímetres s'han incorporat a sondes espacials amb la finalitat d'estudiar les superfícies de planetes i satèl·lits.^[10]^[11]

Altímetre làser

Un altímetre làser o detecció i mesurament d'imatges per làser (LIDAR, de l'anglès light detection and ranging) emet polsos làser (energia en l’ordre de diverses desenes de mil·lijoules per pols) cap a superfícies planetàries amb una freqüència típica de polsos d’entre 10 i 30 Hz. L’instrument mesura el temps d’anada i tornada del pols de llum entre l’emissió i la reflexió retornada per la superfície per determinar la distància de la nau espacial respecte a la superfície. Per tant, funciona de manera molt similar a la tecnologia de radar, que utilitza polsos de radiofreqüència en lloc de polsos de llum. Els polsos làser es generen, per exemple, amb un granat d’alumini d’itri dopat amb neodimi (Nd:YAG), que és bombejat òpticament amb díodes de bombeig làser. L’emissió de polsos làser en el cas del Nd:YAG té lloc a l’infraroig (principalment a 1 064 nm), però, amb dopatges diferents del YAG, també es poden obtenir emissions en l’ultraviolat, el visible o l’infraroig proper. Un làser genera un feix molt estret, emès a través d’una òptica transmissora que introdueix una divergència del feix dissenyada, cosa que permet mapar les característiques de la superfície amb una resolució espacial molt més alta en comparació amb el radar.^[12]

Referències

↑ A Dictionary of Aviation, David W. Wragg. ISBN 0850451639 / ISBN 9780850451634, 1st Edition Published by Osprey, 1973 / Published by Frederick Fell, Inc., NY, 1974 (1st American Edition.)
↑ ^2,0 ^2,1 Arjona Guerrero, A. Proyecto básico de un altímetro barométrico aneroide para su uso en aviación (tesi). Universitat de Sevilla, 2023.
↑ ^3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 ^3,6 Creus Sole, Antonio. Iniciación a la aeronáutica (en castellà). Ediciones Díaz de Santos, 2011-06-09. ISBN 978-84-9969-017-9.
↑ «Diccionari de meteorologia | TERMCAT». [Consulta: 12 novembre 2024].
↑ ^5,0 ^5,1 Bolanakis, Dimosthenis E. MEMS Barometers Toward Vertical Position Detection: Background Theory, System Prototyping, and Measurement Analysis (en anglès). Springer Nature, 2022-05-31. ISBN 978-3-031-79573-2.
↑ ^6,0 ^6,1 Marghany, Maged. Chapter 10 - Modeling wave pattern cycles using advanced interferometry altimeter satellite data. Elsevier, 2021, p. 275–296. ISBN 978-0-12-820785-7.
↑ Wadge, G. REMOTE SENSING | Active Sensors. Oxford: Elsevier, 2005, p. 414–420. ISBN 978-0-12-369396-9.
↑ Hensley, S.; Farr, T. Microwave Remote Sensing and Surface Characterization⋆. Oxford: Academic Press, 2013, p. 30–71. ISBN 978-0-12-818235-2.
↑ «Diccionaris cartogràfics | TERMCAT». [Consulta: 15 novembre 2024].
↑ Wu, Sherman S. C. «Topographic mapping of the Moon». Earth, Moon, and Planets, 32, 2, 4-1985, pàg. 165–172. DOI: 10.1007/bf00054173. ISSN: 0167-9295.
↑ Lorenz, R. D.; Svedhem, H.; Trautner, R.; Kofman, W.; Herique, A. «Observations of the surface of Titan by the Radar Altimeters on the Huygens Probe». Icarus, 270, 15-05-2016, pàg. 248–259. DOI: 10.1016/j.icarus.2015.11.007. ISSN: 0019-1035.
↑ Falkner, P.; Schulz, R. «10.23 - Instrumentation for Planetary Exploration Missions». A: Gerald Schubert. Treatise on Geophysics. 10. 2a. Oxford: Elsevier, 2015, p. 719–755. DOI 10.1016/b978-0-444-53802-4.00181-0. ISBN 978-0-444-53803-1.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Altímetre

[1] A Dictionary of Aviation, David W. Wragg. ISBN 0850451639 / ISBN 9780850451634, 1st Edition Published by Osprey, 1973 / Published by Frederick Fell, Inc., NY, 1974 (1st American Edition.)

[:2-2] 2,0 ^2,1 Arjona Guerrero, A. Proyecto básico de un altímetro barométrico aneroide para su uso en aviación (tesi). Universitat de Sevilla, 2023.

[:1-3] 3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 ^3,6 Creus Sole, Antonio. Iniciación a la aeronáutica (en castellà). Ediciones Díaz de Santos, 2011-06-09. ISBN 978-84-9969-017-9.

[4] «Diccionari de meteorologia | TERMCAT». [Consulta: 12 novembre 2024].

[:0-5] 5,0 ^5,1 Bolanakis, Dimosthenis E. MEMS Barometers Toward Vertical Position Detection: Background Theory, System Prototyping, and Measurement Analysis (en anglès). Springer Nature, 2022-05-31. ISBN 978-3-031-79573-2.

[:3-6] 6,0 ^6,1 Marghany, Maged. Chapter 10 - Modeling wave pattern cycles using advanced interferometry altimeter satellite data. Elsevier, 2021, p. 275–296. ISBN 978-0-12-820785-7.

[7] Wadge, G. REMOTE SENSING | Active Sensors. Oxford: Elsevier, 2005, p. 414–420. ISBN 978-0-12-369396-9.

[8] Hensley, S.; Farr, T. Microwave Remote Sensing and Surface Characterization⋆. Oxford: Academic Press, 2013, p. 30–71. ISBN 978-0-12-818235-2.

[9] «Diccionaris cartogràfics | TERMCAT». [Consulta: 15 novembre 2024].

[10] Wu, Sherman S. C. «Topographic mapping of the Moon». Earth, Moon, and Planets, 32, 2, 4-1985, pàg. 165–172. DOI: 10.1007/bf00054173. ISSN: 0167-9295.

[11] Lorenz, R. D.; Svedhem, H.; Trautner, R.; Kofman, W.; Herique, A. «Observations of the surface of Titan by the Radar Altimeters on the Huygens Probe». Icarus, 270, 15-05-2016, pàg. 248–259. DOI: 10.1016/j.icarus.2015.11.007. ISSN: 0019-1035.

[12] Falkner, P.; Schulz, R. «10.23 - Instrumentation for Planetary Exploration Missions». A: Gerald Schubert. Treatise on Geophysics. 10. 2a. Oxford: Elsevier, 2015, p. 719–755. DOI 10.1016/b978-0-444-53802-4.00181-0. ISBN 978-0-444-53803-1.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]