Arbre binari
En ciències de la computació, un arbre binari és una estructura de dades en la qual cada node sempre té un fill esquerre i un fill dret. No poden tenir més de dos fills (d'ací el nom "binari"). Si algun fill té com a referència null, és a dir que no emmagatzema cap dada, llavors aquest és dit un node extern. En el cas contrari, el fill és dit un node intern.
Usos comuns dels arbres binaris són els arbres binaris de cerca, els monticles binaris i la codificació de Huffman.
Definició de teoria de grafs
[modifica]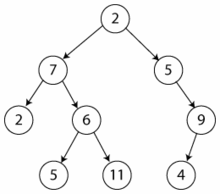
En la teoria de grafs, s'usa la següent definició: «Un arbre binari és un graf connex, acíclic i no dirigit tal que el grau de cada vèrtex no és major a 3». D'aquesta forma només existeix un camí entre un parell de nodes.[1]
Un arbre binari amb arrelat és com un graf que té un dels seus vèrtexs, dit arrel, de grau no major a 2.[2] Amb l'arrel escollida, cada vèrtex tindrà un únic pare, i mai més de dos fills.[3] Si refusem el requeriment de la connectivitat, permetent múltiples components connectats en el graf, anomenarem a aquesta última estructura un bosc.[4]
Tipus d'arbres binaris
[modifica]- Un arbre binari és un arbre amb arrel en la qual cada node té com a màxim dos fills.
- Un arbre binari ple és un arbre en el qual cada node té zero o dos fills.[5][6]
- Un arbre binari perfecte és un arbre binari ple en el qual totes les fulles (vèrtex amb zero fills) estan a la mateixa profunditat (distància des de l'arrel, també dita altura).[7]
- De vegades un arbre binari perfecte és denominat arbre binari complet.[8] Uns altres defineixen un arbre binari complet com un arbre binari ple en el qual totes les fulles estan a profunditat n o n-1, per a alguna n.
Un arbre binari és un arbre en el qual cap node pot tenir més de dos subarbres. En un arbre binari cada node pot tenir zero, un o dos fills (subarbres). Es coneix el node de l'esquerra com a fill esquerre i el node de la dreta com a fill dret.
Implementació en C
[modifica]Un arbre binari pot declarar-se de diverses maneres. Algunes d'elles són:
Estructura amb maneig de memòria dinàmica, sent t el punter que apunta a l'arbre de tipus tTree:
typedef struct tTree {
int key;
struct tTree *hLeft, *hRight;
} tTree;
typedef struct tTree *t;
Estructura amb un vector indexat:
typedef struct tTree {
int key;
int hLeft, hRight;
};
tTree tree[NUMBER_OF_NODES];
En el cas d'un arbre binari quasi-complet (o un arbre complet), pot utilitzar-se un senzill arranjament d'enters amb tantes posicions com nodes haja de tenir l'arbre. La informació de la ubicació del node en l'arbre és implícita a cada posició de l'arranjament. Així, si un node està en la posició *i, els seus fills es troben en les posicions 2i+1 i 2i+2, mentre que el seu pare (si en té), es troba en la posició truncament ((i-1)/2) (suposant que l'arrel està en la posició zero). Aquest mètode es beneficia d'un emmagatzematge més compacte i una millor localitat de referència, particularment durant un recorregut en preordre. L'estructura per a aquest cas seria per tant:
int tree[NUMBER_OF_NODES];
Recorreguts sobre arbres binaris
[modifica]Recorreguts en profunditat
[modifica]El mètode d'aquest recorregut és tractar de trobar de la capçalera a l'arrel en node d'unitat binària Ara passem a veure la implementació dels diferents recorreguts:
Recorregut en preordre
[modifica]En aquest tipus de recorregut es realitza certa acció (potser simplement imprimir per pantalla el valor de la clau d'eixe node) sobre el node actual i posteriorment es tracta el subarbre esquerre i quan s'haja conclòs, el subarbre dret. En l'arbre de la figura el recorregut en preordre seria: 2, 7, 2, 6, 5, 11, 5, 9 i 4.
void preorder(tTree *a) {
if (a != NULL) {
treat(a); // Realitza una operació al node a
preorder(a->hLeft);
preorder(a->hRight);
}
}
Implementació en pseudocodi de forma iterativa:
push(s, NULL); // Inserim en una pila (stack) el valor NULL, per a assegurar-nos que estiga buida push(s, root); // Inserim el node arrel MENTRE (s <> NULL) FER p = pop(s); // Traiem un element de la pila treat(p); // Realitzem operacions sobre el node p SI (I(p) <> NULL) LLAVORS push(s, D(p)); // Si p té arbre dret SI (D(p) <> NULL) LLAVORS push(s, I(p)); // Si p té arbre esquerre FI_MENTRE
Recorregut en postordre
[modifica]En aquest cas es tracta primer el subarbre esquerre, després el dret i finalment el node actual. En l'arbre de la figura el recorregut en postordre seria: 2, 5, 11, 6, 7, 4, 9, 5 i 2.
void postorder(tTree *a) {
if (a != NULL) {
postorder(a->hLeft);
postorder(a->hRight);
treat(a); // Realitza una operació al node a
}
}
Recorregut en inordre
[modifica]En aquest cas es tracta primer el subarbre esquerre, seguit del node actual i finalment el subarbre dret. En un arbre binari de cerca, aquest recorregut donaria els valors clau dels nodes ordenats de menor a major. A l'arbre de la figura, la seqüència de nodes visitats mitjançant aquest recorregut és la següent: 2, 7, 5, 6, 11, 2, 5, 4 i 9.
void inorder(tTree *a) {
if (a != NULL) {
inorder(a->hLeft);
treat(a); // Realitza una operació al node a
inorder(a->hRight);
}
}
Recorreguts en amplitud (o per nivells)
[modifica]En aquest cas el recorregut es realitza en ordre pels diferents nivells de l'arbre. Així, es començaria tractant el nivell 1, que només conté el node arrel, seguidament el nivell 2, el 3 i així successivament. En l'arbre de la figura el recorregut en amplitud seria: 2, 7, 5, 2, 6, 9, 5, 11 i 4.
Al contrari que en els mètodes de recorregut en profunditat, el recorregut per nivells no és de naturalesa recursiva. Per això, s'ha d'utilitzar una cua per a recordar els subarbres esquerres i dret de cada node.
Pseudocodi:
enqueue(root); MENTRE queue_no_buida() FER node = dequeue(); // Treure el node de la cua treat(node); // Realitza una operació al node enqueue_descendents(node); // Fica a la cua els fills del node actual FI_MENTRE
Implementació en C:
void amplitude(tTree *a) {
tQueue queue;
tTree *aux;
if (a != NULL) {
createQueue(queue);
enqueue(queue, a);
while (!emptyQueue(queue)) {
dequeue(queue, aux);
treat(aux) // Realitza una operació al node
if (aux->hLeft != NULL) enqueue(queue, aux->hLeft);
if (aux->hRight!= NULL) enqueue(queue, aux->hRight);
}
}
}
Per a fer un recorregut en amplària, la idea és anar guardant en una cua els fills del node que s'estan visitant i el següent a visitar és el pròxim node de la cua.
Mètodes per a emmagatzemar arbres binaris
[modifica]Els arbres binaris poden ser construïts a partir de llenguatges de programació de diverses formes. En un llenguatge amb registres i referències, els arbres binaris són construïts típicament amb una estructura de nodes i punters en la qual s'emmagatzemen dades, cadascun d'aquests nodes té una referència o punter a un node esquerre i a un node dret denominats fills. A vegades, també conté un punter a un únic node. Si un node té menys de dos fills, alguns dels punters dels fills poden ser definits com a nuls per a indicar que no disposa d'aquest node. En la figura adjunta es pot observar l'estructura d'aquesta implementació.
Els arbres binaris també poden ser emmagatzemats com una estructura de dades implícita en vectors, i si l'arbre és un arbre binari complet, aquest mètode no desaprofita l'espai en memòria. Prendrem com a notació la següent: si un node té un índex i, els seus fills es troben en índexs 2*i + 1 i 2*i + 2, mentre que els seus pares (si els té) es troba en l'índex (partint que l'arrel tinga índex zero). Aquest mètode té com a avantatges el tenir emmagatzemats les dades de forma més compacta i per tenir una forma més ràpida i eficient de localitzar les dades en particular durant un preordre transversal. No obstant això, balafia molt espai en memòria.
Codificació d'arbres n-aris com a arbres binaris
[modifica]Hi ha un mapeig d'un a un entre els arbres generals i arbres binaris, el qual en particular és usat en Lisp per a representar arbres generals com a arbres binaris. Cada node N ordenat en l'arbre correspon a un node N 'en l'arbre binari; el fill de l'esquerra de’ N és el node corresponent al primer fill de N, i el fill dret de N' és el node corresponent al següent germà de N, és a dir, el pròxim node en ordre entre els fills dels pares de N.
Aquesta representació com a arbre binari d'un arbre general, es coneix de vegades com un arbre binari primer fill germà, o un arbre doblement encadenat.
Una manera de pensar sobre açò és que els fills de cada node estiguen en una llista enllaçada, encadenats juntament amb el camp dret, i el node només té un punter al començament o el cap d'aquesta llista, a través del seu camp esquerre.
Per exemple, en l'arbre de l'esquerra, l'A té 6 fills (B, C, D, E, F, G). Pot ser convertit en l'arbre binari de la dreta.
Un exemple de transformar l'arbre n-ari a un arbre binari Com passar d'arbres n-aris a arbres FLOFO.
L'arbre binari pot ser pensat com l'arbre original inclinat cap als costats, amb les vores negres esquerres representant el primer fill i els blaus representat els següents germans.
Les fulles de l'arbre de l'esquerra serien escrites en Lisp com:
(((M N) H I) C D ((O) (P)) F (L))
Que s'executarà en la memòria com l'arbre binari de la dreta, sense cap mena de lletres en aquells nodes que tenen un fill esquerre.
Vegeu també
[modifica]- Arbre (estructura de dades)
- Arbre multibranca
- Arbre binari de cerca
- Arbre de Fibonacci
- Partició d'espai binari
Referències
[modifica]- ↑ Knuth. The Art Of Computer Programming, Volume 1, 3/E. Pearson Education, 1997, p. 363. ISBN 0-201-89683-4.
- ↑ Kenneth Rosen. Discrete Mathematics and Its Applications, 7th edition. McGraw-Hill Science, 2011, p. 749. ISBN 978-0-07-338309-5.
- ↑ Lih-Hsing Hsu; Cheng-Kuan Lin Graph Theory and Interconnection Networks. CRC Press, 2008, p. 66. ISBN 978-1-4200-4482-9.
- ↑ David R. Mazur. Combinatorics: A Guided Tour. Mathematical Association of America, 2010, p. 246. ISBN 978-0-88385-762-5.
- ↑ Richard Stanley, Enumerative Combinatorics, volume 2, p.36
- ↑ Kenneth Rosen. Discrete Mathematics and Its Applications 7th edition. McGraw-Hill Science, 2011, p. 352–353. ISBN 978-0-07-338309-5.
- ↑ «perfect binary tree». NIST.
- ↑ «complete binary tree». NIST.
Bibliografia
[modifica]- Donald Knuth. The Art of Computer Programming vol 1. Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Secció 2.3, especialment sub-seccions 2.3.1–2.3.2 (pp. 318–348).
Enllaços externs
[modifica]- Definicions d'arbres binaris i implementacions en C i Java (anglès)
- Arbre binari de recerca en PHP (castellà)
- Demostració per inducció dels arbres binaris (anglès)
- Balanced binary search tree on array Com crear de baix a dalt una llista d'Ahnentafel, o un arbre de cerca binari equilibrat (anglès)
- Binary trees and Implementation of the same with working code examples (anglès)

