Càlcul de controls de redundància cíclica

Exemple de generació d'un CRC de 8 bits. El generador és un registre de desplaçament de tipus Galois amb portes XOR col·locades segons potències (números blancs) de x en el polinomi del generador. El flux de missatges pot tenir qualsevol longitud. Després que s'hagi desplaçat pel registre, seguit de 8 zeros, el resultat al registre és la suma de control.

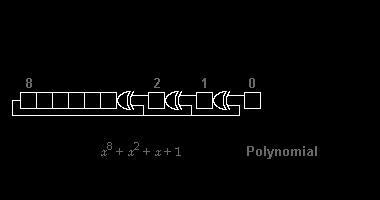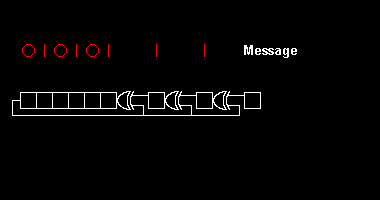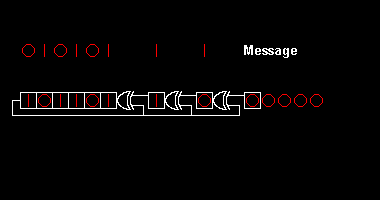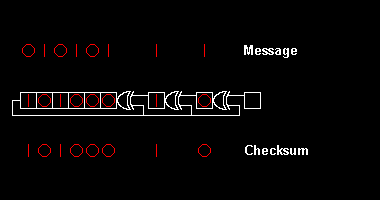
El càlcul d'una comprovació de redundància cíclica es deriva de les matemàtiques de la divisió polinòmica, mòdul dos. A la pràctica, s'assembla a una llarga divisió de la cadena de missatges binari, amb un nombre fix de zeros afegits, per la cadena "polinomi generador", excepte que l'exclusiva o les operacions substitueixen les restes. La divisió d'aquest tipus es realitza de manera eficient en maquinari mitjançant un registre de desplaçament modificat, i en programari mitjançant una sèrie d' algorismes equivalents, començant amb un codi senzill proper a les matemàtiques i fent-se més ràpid (i possiblement més ofuscat ) a través de byte. paral·lelisme intel·ligent i compensacions espai-temps.

Comprovació de les dades rebudes amb checksum. El missatge rebut es desplaça pel mateix registre que s'utilitza al generador, però la suma de comprovació rebuda s'hi adjunta en lloc de zeros. Les dades correctes donen el resultat de tots zeros; un bit danyat en el missatge o la suma de comprovació donaria un resultat diferent, advertint que s'ha produït un error.

Diversos estàndards CRC amplien l'algoritme de divisió polinòmica especificant un valor inicial de registre de desplaçament, un pas final d'O exclusiu i, el més crític, una ordenació de bits (endianness). Com a resultat, el codi vist a la pràctica es desvia de manera confusa de la divisió "pura", i el registre pot desplaçar-se cap a l'esquerra o cap a la dreta.

Exemple

Com a exemple d'implementació de la divisió polinomial al maquinari, suposem que estem intentant calcular un CRC de 8 bits d'un missatge de 8 bits fet del caràcter ASCII "W", que és binari 01010111₂, decimal 87 ₁₀ o hexadecimal 57 ₁₆. Per il·lustració, utilitzarem el polinomi CRC-8-ATM (HEC). $x^{8}+x^{2}+x+1$. Escriure el primer bit transmès (el coeficient de la potència més alta de $x$ ) a l'esquerra, correspon a la cadena de 9 bits "100000111".

El valor del byte 57 ₁₆ es pot transmetre en dos ordres diferents, depenent de la convenció d'ordenació de bits utilitzada. Cadascun genera un polinomi de missatge diferent $M(x)$. Msbit primer, això és $x^{6}+x^{4}+x^{2}+x+1$ = 01010111, mentre que lsbit-primer, ho és $x^{7}+x^{6}+x^{5}+x^{3}+x$ = 11101010. Després es poden multiplicar per $x^{8}$ per produir dos polinomis de missatges de 16 bits $x^{8}M(x)$.

El càlcul de la resta consisteix llavors a restar múltiples del polinomi generador $G(x)$. Això és com una divisió llarga decimal, però encara més senzill perquè els únics múltiples possibles a cada pas són 0 i 1, i les restes prenen prestades "de l'infinit" en lloc de reduir els dígits superiors. Com que no ens importa el quocient, no cal registrar-lo.

Most-significant bit first

0 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 − 0 0 0 0 0 0 0 0 0 = 0 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 − 1 0 0 0 0 0 1 1 1 = 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 0 − 0 0 0 0 0 0 0 0 0 = 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 0 − 1 0 0 0 0 0 1 1 1 = 0 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 − 0 0 0 0 0 0 0 0 0 = 0 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 − 1 0 0 0 0 0 1 1 1 = 0 0 0 0 0 0 1 0 1 0 1 0 1 1 0 0 − 1 0 0 0 0 0 1 1 1 = 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 − 0 0 0 0 0 0 0 0 0 = 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0

Observeu que després de cada resta, els bits es divideixen en tres grups: al principi, un grup que és tot zero; al final, un grup que no canvia respecte a l'original; i un grup ombrejat blau al mig que és "interessant". El grup "interessant" té una longitud de 8 bits, que coincideix amb el grau del polinomi. A cada pas, es resta el múltiple adequat del polinomi per fer el grup zero un bit més llarg, i el grup sense canvis es fa un bit més curt, fins que només queda la resta final.

En l'exemple msbit-primer, el polinomi restant és $x^{7}+x^{5}+x$. Convertint a un nombre hexadecimal utilitzant la convenció que la potència més alta de x és el msbit; això és A2 ₁₆. A lsbit-first, la resta és $x^{7}+x^{4}+x^{3}$. Convertint a hexadecimal utilitzant la convenció que la potència més alta de x és lsbit, això és 19 ₁₆.

Implementació

Escriure el missatge complet a cada pas, tal com es fa a l'exemple anterior, és molt tediós. Les implementacions eficients utilitzen un $n$ -Registre de desplaçament de bits per contenir només els bits interessants. Multiplicant el polinomi per $x$ equival a desplaçar el registre d'un lloc, ja que els coeficients no canvien de valor sinó que només es mouen cap al següent terme del polinomi.

Aquí teniu un primer esborrany d'algun pseudocodi per calcular un CRC de n bits. Utilitza un tipus de dades compost per a polinomis, on x no és una variable entera, sinó un constructor que genera un objecte polinomi que es pot afegir, multiplicar i exponenciar. A xor dos polinomis és sumar-los, mòdul dos; és a dir, excloure OR els coeficients de cada terme coincident dels dos polinomis.