Cúpula (geometria)
|
|
Aquest article o secció no cita les fonts o necessita més referències per a la seva verificabilitat. |
 | |
| Tipus | prismatoide i políedre convex |
|---|---|
| Forma de les cares | 1 n-gone 1n triangles n carrés 2n-gone |
| Simetria | Cnv |
| Propietats | convexe |
| Elements | |
| Cares | 2n+2 |
| Arestes | 5n |
| Vèrtexs | 3n |
| Més informació | |
| MathWorld | Cupola |
En geometria, una cúpula és un sòlid format ajuntant dos polígons, un (la base) amb el doble d'arestes que l'altre, i per una banda alternada de triangles i de rectangles. Si els triangles són equilaterals i els rectangles són quadrats, mentre que la base i la seva cara oposada són polígons regulars, llavors la cúpula és un sòlid de johnson. Les cúpules triangular, quadrada i pentagonal poden ser formades prenent seccions del cuboctaèdre, del petit rhombicuboctaèdre i del petit rhombicosidodécaèdre, respectivament.
L'alçada d'una cúpula 2n-gonal és igual a l'alçada d'una piràmide n-gonal (aquesta regla també és certa per als casos extrems del prisma triangular i de la cúpula dodecagonal).
Una cúpula pot ser vista com un prisma, en què un dels polígons ha estat reduït a un de la meitat de costats fusionant vèrtx alterns. Les cúpules són una subclasse dels prismatoïdes.
Exemples
[modifica] |
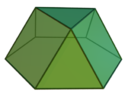 |
 |
 |

Els tres políedres esmentats més amunt són les úniques cúpules no trivials amb cares regulars: la «cúpula dodecagonal» és una figura plana, i el prisma triangular pot ser considerat com una «cúpula» de grau 2 (la cúpula d'un segment i d'un quadrat). No obstant això, les cúpules de polígons de graus més elevats poden ser construïdes amb cares triangulars i rectangulars irregulars.
Coordenades dels vèrtexs
[modifica]La definició d'una cúpula no requereix que la base sigui un polígon regular (o el costat oposat a la base que es pot anomenar sostre), però és pràctic considerar el cas en què la cúpula posseeix la seva simetria màxima, Cnv. En aquest cas, el sostre és un n-gon regular, mentre que la base sigui un 2n-gon regular o un 2n-gon que posseeix dues longituds de costat diferents que s'alternen i els mateixos angles que un 2n-gon regular. És pràctic fixar el sistema de coordenades tal que la base sigui col·locada en el pla xy, amb el sostre en un pla paral·lel al pla xy. Els plans de simetria especular passen a través de l'eix z i comparteixen els costats de la base. Parteixen també ja sigui els costats o els vèrtexs del sostre o tots dos (si no és parell, la meitat dels plans de simetria especular parteixen els costats del polígon del sostre i la meitat parteix els vèrtexs, si és senar, cada pla de simetria especular parteix un costat i un angle del polígon del sostre). El vèrtex de la base poden ser designats per V1 fins a V2n, mentre que els vèrtexs del polígon del sostre poden ser designats per V2n+1 fins a V3n. Amb aquestes convencions, les coordenades dels vèrtexs poden ser escrites com:
V2j-1: (rbcos [2π(j-1)/n + α], rbsin [2π(j-1)/n + α], 0) (on j=1, 2, …, n);
V2j: (rbcos (2πj/n - α), rbsin (2πj/n - α), 0) (on j=1, 2, …, n);
V2n+j: (rtcos (πj/n), rtsin (πj/n), h) (on j=1, 2, …, n),
ja que els polígons V1V₂V2n+1V2n+2, etc. són rectangles, això imposa una restricció sobre els valors de rb, rt i α. La distància V1V2 és igual a:
rb{[cos (2π/n - α) – cos α]² + [sin (2π/n - α) - sin α] 2}1/2
= rb{[cos ² (2π/n - α) – 2cos (2π/n - α)cos α + cos² α] + [sin ² (2π/n - α) – 2 sin (2π/n - α)sin α + sin ²α]}1/2
= rb{2[1 – cos (2π/n - α)cos α – sin (2π/n - α)sin α]}1/2
= rb{2[1 – cos (2π/n - 2α)]}1/2,
mentre que la distància V2n+1V2n+2 és igual a:
rt{[cos (π/n) – 1]² + sin²(π/n)}1/2
= rt{[cos² (π/n) – 2cos (π/n) + 1] + sin²(π/n)}1/2
= rt{2[1 – cos (π/n)]}1/2.
Aquestes són iguals, i si l'aresta comuna es nota per s,
rb = s/{2[1 – cos (2π/n - 2α)]}1/2
rt= s/{2[1 – cos (π/n)]}1/2
Aquests valors s'han d'inserir en les expressions per a les coordenades dels vèrtexs donades més amunt.
Generalització a dimensió 4
[modifica]
Les cúpules poden ser obtingudes per una «expansió» de les piràmides corresponents (exemple: la piràmide quadrada dona la cúpula quadrada): les cares triangulars de les piràmides són progressivament separades intercalant rectangles fins que aquests siguin quadrats. La base n-gonal de la piràmide es transforma, doncs, en una base 2n-gonal, i el vèrtex de la piràmide dona lloc a un n-gon.
Aquesta propietat implica que l'alçada d'una cúpula 2n-gonal és la mateixa que la de la piràmide n-gonal.
Per generalitzar les cúpules en dimensió 4, cal doncs partir d'una piràmide 4d i aplicar aquesta mateixa expansió: s'obtenen sempre una base i un sostre enllaçats entre ells per piràmides (que reemplacen els triangles) i prismes (que reemplacen els quadrats).
Com saber quina base correspon a quin sostre? Es tracta sempre d'una expansió de la base de la piràmide. Així, en dimensió 2, l'operació d'expansió corresponia de fet a un truncament: és pel que[Cal aclariment] es connecta un n-gone a un 2n-gone; en dimensió 3, l'expansió s'anomena «xanfranatge» (cantellation en anglès); si es volgués ampliar fins a dimensió 5, l'expansió pren el nom (en anglès) de «runcination» després «sterication» (vegeu la pàgina anglesa Expansion (geometry)).
El xanfranatge d'un tétraèdre dona un cuboctàedre. La cúpula corresponent és, doncs, la cúpula tétraèdrica, que té per a la base un cuboctaèdre i per al sostre un tétraèdre.
Igual com 2 cúpules hexagonals donen un cuboctaèdre, 2 cúpules tétraédriques donen un pentacor «runcinat» (runcinated pentachoron en anglès).
Existeixen en total 4 hiperpiràmides regulars, existeix doncs 4 hipercúpules regulars: la cúpula tétrahèdrica, la cúpula cúbica, la cúpula octaèdrica i la cúpula dodécahèdrica.
Hipercúpula
[modifica]La casella corresponent a poliedres de la taula presenta les dades en el següent ordre:
- El sostre.
- Els poliedres que uneixen les cares de la base a les cares del sostre.
- Els poliedres que uneixen les cares de la base a les arestes del sostre.
- Els poliedres que uneixen les cares de la base als vèrtexs del sostre.
- La base.

|

|

|
||||||
| Tipus | ||||||||
| Vèrtex | ||||||||
| Arestes | ||||||||
| Cares | 18 quadrats |
48 quadrats |
42 quadrats |
90 cares 24 pentàgons | ||||
| Políedres | 4 prismes triangulars 6 prismes triangulairs 4 tetraèdres 1 Cuboctàedre |
6 cubs 12 prismes triangulars 8 tetraèdres 1 rombicuboctàedre |
8 prismes triangulars 12 prismes triangulars 6 piràmides cares 1 rhombicuboctaèdre |
12 prismes pentagonals 30 prismes triangulars 20 tetraèdres 1 rombi-cosidodecàedre | ||||
