Corba de Lebesgue

Primeres iteracions de la corba de Lebesgue.

La corba de Lebesgue és una corba fractal contínua que recobreix el pla i és derivable gairebé a tots els punts, introduïda per Henri Lebesgue l'any 1905. També s'anomena corba de Morton per Guy Macdonald Morton, el primer informàtic de dades que va fer-la servir per emmagatzemar dades de forma seqüencial, com a mapatge de dades multidimensionals a una única dimensió preservant la localitat dels punts de dades propers. Aquest mapatge és efectiu perquè la corba correspon al valor z d'un punt multidimensional, és a dir, una estructura intercalada de les representacions binàries dels seus valors de coordenades; per aquest motiu també se l'anomena corba d'ordre z. Un cop ordenades les dades en aquest ordre, es pot utilitzar qualsevol estructura de dades unidimensionals, com ara arbres de cerca binària, arbres B, skip lists o taules hash. L'ordenació resultant es pot descriure de manera equivalent com l'ordre que s'obtindria d'un primer recorregut de profunditat d'un quadtree.

Procediment

La corba es pot obtenir dividint un pla en quatre quadrants i unint els punts centrals de cada quadrant d'esquerra a dreta i de dalt a baix ordenadament, formant una Z. Per obtenir la corba d'ordre següent, es divideix de nou cadascun dels quadrants en quatre parts i s'hi aplica el mateix procediment, i finalment s'uneix el punt final de la Z de cada quadrant amb l'inicial del següent. Per tant, el nombre de punts per un ordre n és 4ⁿ. Aquesta construcció evidencia que la corba és autosimilar respecte l'ordre anterior, excepte les línies d'unió entre els quadrants principals.

Generalització per dimensions superiors

Corba de Lebesgue tridimensional
Primer ordre	Segon ordre	Tercer ordre

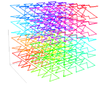La corba es pot generalitzar per dimensions superiors aplicant el mateix procediment. En el cas de tres dimensions, a cada pas es divideix cada cub en 8 cubs i se n'uneixen els punts centrals en ordre binari.

Relació amb el conjunt de Cantor

Analíticament, la corba està relacionada amb el conjunt de Cantor i la funció esglaonada. Els nombres del conjunt de Cantor admeten una expansió ternària per tal de ser mapats en un quadrat $[0,1]\times [0,1]$ de forma que per cada valor $y\in Y$ hi ha una $x\in X$ a la qual correspon aquesta $y$.

Aquesta propietat implica que en el mapatge $f:C\rightarrow [0,1]\times [0,1]$, les dues coordenades de qualsevol punt $(x,y)$ al quadrat de la unitat admeten una expansió binària; les dues es poden entrellaçar en un sol membre de $C$ en un revers de la definició de $f$.

Lebesgue va ampliar el mapatge de $f$ amb una interpolació lineal de $C$ a $[0,1]$ per construir la funció esglaonada de Cantor. Definint $(a,b)$ com un dels intervals eliminats en la construcció del conjunt de Cantor, llavors per $t\in (a,b)$:

$f(t)={\frac {1}{b-a}}(f(b)(t-a)+f(a)(b-t))$.

La funció és diferenciable a tot interval $(a,b)$, i com que la mesura ("llargada") del conjunt és 0, és diferenciable gairebé a tot l'interval unitari $[0,1]$.

Vegeu també

• Corba de Peano
• Corba de Hilbert

Bibliografia

• Sagan, H. Space-Filling Curves. Springer-Verlag, 1994. 

Enllaços externs

• Plane Filling Curves: the Lebesgue Curve - Cut The Knot (anglès)
• Lebesgue 3D Curves - Visualització de la versió tridimensional de la corba