Criteri de Kelly

Exemple de la fracció òptima d'apostes de Kelly, enfront del rendiment esperat d'altres apostes fraccionades.

En teoria de la probabilitat, el criteri de Kelly (o estratègia de Kelly o aposta de Kelly), és una fórmula per dimensionar una aposta. La mida de l'aposta de Kelly es troba maximitzant el valor esperat del logaritme de la riquesa, que equival a maximitzar la taxa de creixement geomètrica esperada. Se suposa que els rendiments esperats són coneguts i és òptim per a un apostant que valora la seva riquesa de manera logarítmica. J. L. Kelly Jr, un investigador dels Bell Labs, va descriure el criteri el 1956. Com que el criteri de Kelly condueix a una riquesa més gran que qualsevol altra estratègia a llarg termini (és a dir, el rendiment màxim teòric a mesura que el nombre d'apostes arriba a l'infinit), és un mètode científic d'apostes.

S'ha demostrat l'ús pràctic de la fórmula per als jocs d'atzar i la mateixa idea es va utilitzar per explicar la diversificació en la gestió d'inversions. A la dècada de 2000, l'anàlisi a l'estil Kelly es va convertir en una part de la teoria de la inversió i s'ha afirmat que els inversors d'èxit com Warren Buffett i Bill Gross usen mètodes Kelly.

Exemple d'apostes òptimes

En un estudi, a cada participant se li van donar 25 dòlars i se li va demanar que fes apostes a cara o creu amb una moneda que donaria cara el 60% de les vegades. Els participants tenien 30 minuts per jugar, així que podien fer unes 300 apostes, i els premis tenien un límit de 250 dòlars. Però el comportament dels subjectes de prova estava lluny de ser òptim:

«

Sorprenentment, el 28% dels participants van fallar i el retorn mitjà va ser de només 91 dòlars. Només el 21% dels participants van assolir el màxim. 18 dels 61 participants ho van apostar tot en un sol llançament, mentre que dos terços van jugar creu en algun moment de l'experiment.

»

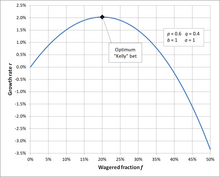
Fent servir el criteri de Kelly i basant-se en les probabilitats de l'experiment (ignorant el límit de 250 dòlars i la durada finita de la prova), l'enfocament correcte seria apostar el 20% de la liquiditat a cada llançament de la moneda, que resulta en un guany mitjà del 2,034% a cada ronda. Aquesta és una mitjana geomètrica, no la taxa aritmètica del 4% ($r=(1+0.2\cdot 1.0)^{0.6}\cdot (1-0.2\cdot 1.0)^{0.4}$).

El benefici esperat teòric després de 300 rondes arriba a 10.505 dòlars ($=25\cdot (1.02034)^{300}$) si no hi ha límit.

En aquest joc en particular, a causa del límit, una estratègia d'apostar només el 12% del pot en cada llançament tindria resultats encara millors (una probabilitat del 95% d'assolir el límit i un retorn mitjà de 242,03 dòlars).

Fórmula en apostes

Quan perdre l'aposta implica perdre tota l'aposta, l'aposta Kelly és:

$f^{*}=p-{\frac {q}{b}}=p-{\frac {1-p}{b}}$

on:

• $f^{*}$ és la fracció d'efectiu actual a apostar.
• $p$ és la probabilitat de guanyar.
• $q$ és la probabilitat de perdre ($q=1-p$).
• $b$ és la proporció de l'aposta guanyada amb una victòria. Per exemple, si aposteu 10 dòlars en una aposta de 2 a 1 (en guanyar, us retornarà 30 dòlars, guanyant 20 dòlars), aleshores $b=\$20/\$10=2.0$.