Deformació temporal dinàmica

Deformació temporal dinàmica entre dues funcions lineals a trossos. La línia de punts il·lustra la relació de deformació temporal. Observeu que diversos punts de la funció inferior s'assignen a un punt de la funció superior i viceversa.

En l'anàlisi de sèries temporals, la deformació temporal dinàmica (DTW) és un algorisme per mesurar la similitud entre dues seqüències temporals, que poden variar en velocitat. Per exemple, es podrien detectar similituds en caminar amb DTW, fins i tot si una persona caminava més ràpid que l'altra, o si hi hagués acceleracions i desacceleracions durant el transcurs d'una observació. DTW s'ha aplicat a seqüències temporals de dades de vídeo, àudio i gràfics; de fet, qualsevol dada que es pugui convertir en una seqüència unidimensional es pot analitzar amb DTW. Una aplicació coneguda ha estat el reconeixement automàtic de la veu, per fer front a diferents velocitats de parla. Altres aplicacions inclouen el reconeixement de parlants i el reconeixement de signatures en línia. També es pot utilitzar en aplicacions de concordança de formes parcials.

Dues repeticions d'una seqüència de caminada gravades amb un sistema de captura de moviment. Tot i que hi ha diferències en la velocitat de caminar entre repeticions, els camins espacials de les extremitats segueixen sent molt similars.

En general, DTW és un mètode que calcula una concordança òptima entre dues seqüències donades (per exemple, sèries temporals) amb certes restriccions i regles:

• Cada índex de la primera seqüència ha de coincidir amb un o més índexs de l'altra seqüència, i viceversa.
• El primer índex de la primera seqüència ha de coincidir amb el primer índex de l'altra seqüència (però no ha de ser la seva única coincidència)
• L'últim índex de la primera seqüència ha de coincidir amb l'últim índex de l'altra seqüència (però no ha de ser la seva única coincidència)
• El mapatge dels índexs de la primera seqüència als índexs de l'altra seqüència ha de ser monòtonament creixent, i viceversa, és a dir, si són índexs de la primera seqüència, llavors no hi ha d'haver dos índexs en l'altra seqüència, tal que l'índex coincideix amb l'índex i índex coincideix amb l'índex , i viceversa

  

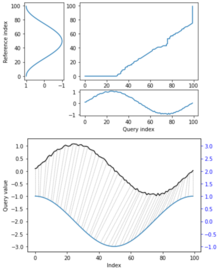
  DTW entre una sinusoide i una versió sorollosa i desplaçada.

Podem representar cada coincidència entre les seqüències $1:M$ i $1:N$ com un camí en a $M\times N$ matriu de $(1,1)$ a $(M,N)$, de manera que cada pas és un dels $(0,1),(1,0),(1,1)$. En aquesta formulació, veiem que el nombre de coincidències possibles és el nombre de Delannoy.

La concordança òptima és la coincidència que compleix totes les restriccions i les regles i que té el cost mínim, on el cost es calcula com la suma de diferències absolutes, per a cada parell d'índexs coincidents, entre els seus valors.

Les seqüències es "deforman" de manera no lineal en la dimensió temporal per determinar una mesura de la seva similitud independent de certes variacions no lineals en la dimensió temporal. Aquest mètode d'alineació de seqüències s'utilitza sovint en la classificació de sèries temporals. Tot i que DTW mesura una quantitat semblant a una distància entre dues seqüències donades, no garanteix que es mantingui la desigualtat del triangle.

A més d'una mesura de similitud entre les dues seqüències, es produeix un anomenat "camí de deformació". Deformant-se segons aquest camí, els dos senyals es poden alinear en el temps. El senyal amb un conjunt original de punts X (original), Y (original) es transforma en X (deformat), Y (deformat). Això troba aplicacions en la seqüència genètica i la sincronització d'àudio. En una tècnica relacionada, es poden promediar seqüències de velocitat variable utilitzant aquesta tècnica, vegeu la secció de seqüències mitjanes.

Això és conceptualment molt similar a l'algorisme de Needleman-Wunsch.

Aplicacions

Reconeixement de paraules parlades

A causa de les diferents velocitats de parla, es produeix una fluctuació no lineal en el patró de parla en funció de l'eix del temps, que s'ha d'eliminar. La concordança DP és un algorisme de concordança de patrons basat en la programació dinàmica (DP), que utilitza un efecte de normalització del temps, on les fluctuacions en l'eix del temps es modelen mitjançant una funció de deformació temporal no lineal. Tenint en compte dos patrons de parla qualsevol, podem desfer-nos de les seves diferències de temps deformant l'eix del temps d'un de manera que s'assoleixi la màxima coincidència amb l'altre. A més, si es permet que la funció de deformació prengui qualsevol valor possible, es pot fer menys distinció entre paraules que pertanyen a categories diferents. Així doncs, per millorar la distinció entre paraules pertanyents a diferents categories, es van imposar restriccions al pendent de la funció de deformació.

Anàlisi de la potència de correlació

Els rellotges inestables s'utilitzen per derrotar l'anàlisi de potència ingènua. S'utilitzen diverses tècniques per contrarestar aquesta defensa, una de les quals és la deformació del temps dinàmica.

Finances i econometria

La deformació temporal dinàmica s'utilitza en finances i econometria per avaluar la qualitat de la predicció en comparació amb les dades del món real.