Efecte Doppler
L'efecte Doppler és el canvi de freqüència aparent d'una ona produït pel moviment relatiu de la font respecte al seu observador.[1][2] Aquest fenomen es va anomenar en honor del físic austríac Christian Andreas Doppler, qui el va descriure el 1842. El nom efecte Doppler-Fizeau es reserva per a les ones electromagnètiques.
El motiu de l'efecte Doppler és que quan la font de les ones es desplaça cap a l'observador, cada cresta d'ona successiva s'emet des d'una posició més propera a l'observador que la cresta de l'ona anterior i, per tant, cada ona triga una mica menys en arribar a l'observador que l'ona anterior, de manera que es redueix el temps entre l'arribada de successives crestes d'ona a l'observador, provocant un augment de la freqüència.[3] Mentre viatgen, la distància entre els fronts successius d'ones es redueix, de manera que les ones «s'agrupen». Per contra, si la font d'ones s'allunya de l’observador, cada ona s'emet des d’una posició més allunyada de l’observador que l’ona anterior, de manera que el temps d’arribada entre ones successives augmenta, reduint la freqüència. Mentre viatgen, s'incrementa la distància entre els successius fronts d'ona, de manera que les ones «s'estenen».
Hi ha exemples quotidians de l'efecte Doppler en què la velocitat a la qual es mou l'objecte que emet les ones és comparable a la velocitat de propagació d'aquestes ones. La velocitat d'una ambulància (50 km/h) pot semblar insignificant respecte a la velocitat del so al nivell de la mar (uns 1235 km/h), però, es tracta d'aproximadament un 4% de la velocitat del so, fracció prou gran com per provocar que s'apreciï clarament el canvi del so de la sirena des d'un to més agut a un de més greu, just en el moment en què el vehicle passa a la vora de l'observador.
-
Efecte Doppler produït per un vehicle en moviment
En el cas de l'espectre visible de la radiació electromagnètica, si l'objecte s'allunya, la seva llum es desplaça a longituds d'ona més llargues, produint-se un desplaçament cap al roig. Si l'objecte s'apropa, la seva llum presenta una longitud d'ona més curta, desplaçant cap al blau. Aquesta desviació cap al vermell o el blau és molt lleu fins i tot per a velocitats elevades, com les velocitats relatives entre estrelles o entre galàxies, i l'ull humà no pot captar-lo, només mesurar-lo indirectament utilitzant instruments de precisió com espectròmetres. El fet que el desplaçament cap al vermell sigui més pronunciat en les galàxies més llunyanes va ajudar a formular la teoria de l'expansió de l'univers i del big-bang.[1]
-
Desplaçament cap al roig o cap al blau en funció del moviment relatiu entre l'objecte emissor i l'observador
-
El mètode de la velocitat radial per detectar exoplanetes es basa en el efecte Doppler
-
Imatge del telescopi espacial Hubble, on es pot veure de desplaçament cap al roig de les galàxies llunyanes.
Si l'objecte emissor es mogués a fraccions significatives de la velocitat de la llum, sí seria apreciable de forma directa la variació de longitud d'ona.
Per a ones que es propaguen en un medi, com ara les ones sonores, la velocitat de l'observador i de la font és relativa al medi en què es transmeten les ones.[2] Per tant, l'efecte Doppler total pot resultar del moviment de la font, del moviment de l'observador o del moviment del medi. Cadascun d’aquests efectes s'analitza per separat. Per a ones que no necessiten un medi, com la llum o la gravetat en la relativitat general, només cal tenir en compte la diferència de velocitat relativa entre l'observador i la font.
Història
[modifica]Christian Andreas Doppler va proposar aquest efecte el 1842 en el seu tractat Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la llum en estrelles binàries i altres astres).[4]
-
Efecte Doppler d’una font de so en moviment
-
Experiment de C.H.D. Buys Ballot (1845) representat en un mur a Utrecht (2019)
El científic neerlandès Christoph Hendrik Diederik Buys Ballot va investigar aquesta hipòtesi el 1845 per al cas d'ones sonores (utilitzant músics que tocaven una nota determinada en un tren de la línia Utrecht-Amsterdam), i va confirmar que el to d'un so emès per una font que s'aproxima a l'observador és més agut que si la font s'allunya. Hippolyte Fizeau va descobrir independentment el mateix fenomen en el cas d'ones electromagnètiques en 1848. A Gran Bretanya, John Scott Russell va fer un estudi experimental de l'efecte Doppler el 1848.[5]
A França aquest efecte es coneix com a «efecte Doppler-Fizeau» i als Països Baixos com «efecte Doppler-Gestirne».[6]
Conceptes generals
[modifica]En física clàssica, on les velocitats de l'emissor (també anomenat «font») i del receptor (o també «observador») pel que fa al medi són inferiors a la velocitat de les ones en el propi medi, la relació entre la freqüència observada i la freqüència emesa ve donada per:[7]
- on
- és la velocitat de les ones en el medi (no és necessàriament la velocitat de la llum);
- és la velocitat del receptor (observador) en relació amb el medi (positiva si el receptor s'apropa cap a l'emissor, i negativa si s'allunya);
- és la velocitat de l'emisor (font) en relació al medi (positiva si l'emisor s'allunya del receptor, i negativa si s'apropa).
(Conclusió: la freqüència augmenta quan font i observador s'apropen entre ells, i es redueix quan s'allunyen).
En la fórmula anterior se suposa que la font està apropant-se (o allunyant-se) «directament» de l'observador. Si la font s'apropa a l'observador amb velocitat constant, però en una trajectòria «no incident» (com per exemple, un avió en vol respecte a un observador situat en terra), llavors:
- La freqüència que l'observador escolta primer és més alta que la freqüència emesa des de l'objecte.
- A continuació es produeix una disminució gradual de la freqüència percebuda a mesura que la font s'apropa a l'observador, coincidint la freqüència percebuda amb l'original quan l'ona arriba des d'una direcció perpendicular al moviment relatiu (és a dir, quan va ser emesa des del punt més proper a l'observador, encara que quan es rebi l'ona, la font i l'observador ja no estaran en la posició més propera).
- Finalment, l'observador percebrà una contínua disminució de la freqüència a mesura que s'allunya la font.
Quan el receptor es troba a tocar de la trajectòria de l'emisor, la transició d'alta a baixa freqüència és molt abrupta. En canvi, quan el receptor està lluny de la trajectòria de l'emisor, la transició d'alta a baixa freqüència és gradual.
Si les velocitats i són petites en comparació amb la velocitat de l'ona , la relació entre la freqüència observada i la freqüència emesa és aproximadament[7]
| Freqüència observada | Canvi de freqüència |
|---|---|
- on
- és el contrari de la velocitat del receptor respecte a l'emisor; és positiu quan l'emisor i el receptor s'apropen entre ells
Demostració:Donat
dividint per
A partir de es pot deduir l'expressió geomètrica:
Anàlisis
[modifica]Per entendre el que succeeix, consideri la següent analogia. Algú llança una bola cada segon a un home. S'assumeix que les boles viatgen amb velocitat constant. Si el llançador està aturat, l'home rebrà una bola cada segon. No obstant això, si el llançador s'està movent cap a l'home, aquest rebrà les boles amb més freqüència a causa que les boles es trobaran menys espaiades. L'invers és cert si el llançador s'allunya de l'home. Per tant, en realitat és la longitud d'ona la que es veu afectada; com a conseqüència, la freqüència rebuda també es veu afectada. També es pot afirmar que la velocitat de l'ona roman constant, mentre que es produeixen canvis en la longitud d'ona; i per tant, la freqüència també canvia.
-
Un micròfon immòbil registra les sirenes dels automòbils de policia en moviment en diversos tons, depenent de la seva direcció relativa
Per a un observador en repòs respecte al medi, si una font en moviment està emetent ones amb una freqüència real donada (en aquest cas, la longitud d'ona canvia però la velocitat de transmissió de l'ona es manté constant, de manera que la velocitat de transmissió de l'ona no depèn de la velocitat de la font), llavors l'observador detecta ones amb una freqüència donada per:
Una anàlisi similar per a un observador en moviment i una font estacionària (en aquest cas, la longitud d'ona es manté constant, però a causa del moviment de l'observador, la velocitat a la qual l'observador rep les ones i, per tant, la velocitat de transmissió de l'ona (pel que fa a l'observador) canvia), produeix la freqüència observada:

Això es pot generalitzar en l'equació que es va presentar a la secció anterior, per al cas d'un observador en moviment i una font en moviment (en aquest cas, la longitud d'ona es manté constant, però, a causa del moviment, la velocitat a la qual l'observador rep ones i, per tant, la velocitat de transmissió de l'ona (respecte de l'observador) canvia) produeix la freqüència observada:
- ×
En el cas d'un observador estacionari i una font que es mou a la velocitat del so, l'equació Doppler preveu una freqüència infinita momentània percebuda per un observador davant d’una font que viatja a la velocitat del so. Tots els pics estan al mateix lloc, de manera que la longitud d'ona és zero i la freqüència és infinita. Aquesta superposició de totes les ones produeix una ona de xoc que per a les ones sonores es coneix com a bang sònic. Quan la font es mou més ràpidament que la velocitat de l’ona, la font supera l’ona i l'equació pot donar valors de freqüència negatius, però -500 Hz és gairebé el mateix que +500 Hz pel que fa a un observador.
Un efecte interessant va ser predit per Lord Rayleigh en el seu llibre clàssic sobre el so: «si la font s'apropa a l'observador a dues vegades la velocitat del so, una peça musical emesa per aquesta font se sentiria en el temps i to correcte, però a l'inrevés» (és a dir, les notes de la fi de la peça arribarien a l'observador abans que les del seu començament).[8]
L'efecte Doppler sobre el so només es percep clarament amb objectes movent-se a força velocitat; el canvi en la freqüència de to musical implica una velocitat de prop de 40 m/s (144 km/h). No obstant això, els canvis d'amplitud dels sons dels emissors en moviment poden ser fàcilment confosos amb petits canvis en la freqüència. Neil A Downie ha demostrat com l'efecte Doppler pot fer-se molt més fàcilment audible mitjançant l'ús d'un emissor ultrasònic (per exemple, de 40 kHz) emetent des d'objectes en moviment. L'observador ha d'utilitzar un convertidor de freqüència heterodí (com els que s'utilitzen en molts detectors de ratpenats) amb capacitat per treballar en la banda de fins als 40 kHz. En aquest cas, amb el receptor ajustat per traduir les ones rebudes a la banda dels 2000 Hz per fer-les audibles, només cal que l'emissor es desplaci a tan sols 2 m/s perquè l'observador percebi un desplaçament de freqüència d'un to sencer (240 Hz).
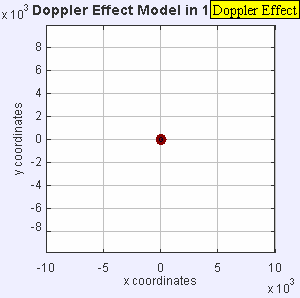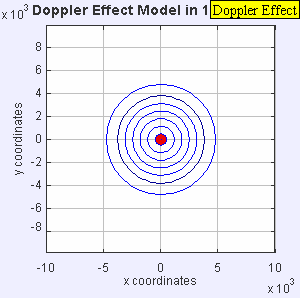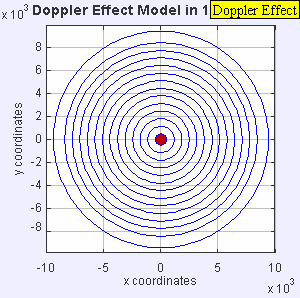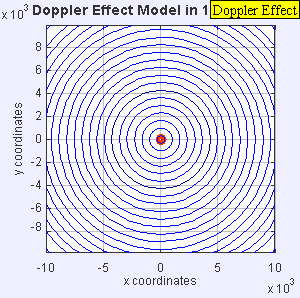
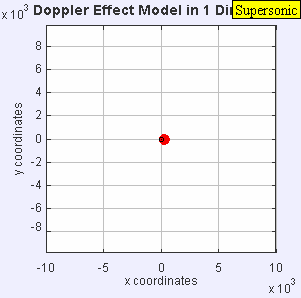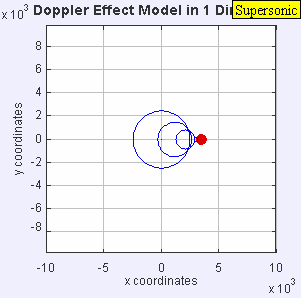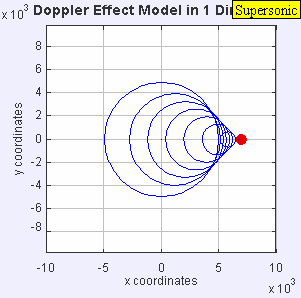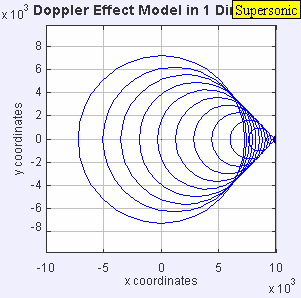
Situació estacionària, subsònica, sònica i supersònica
[modifica]En els quatre gràfics següents s'inclou una animació amb l'anàlisi del comportament de les ones sonores en els quatre casos característics de l'efecte Doppler en relació amb la velocitat de l'emissor respecte a la velocitat de propagació del so en l'aire (Mach 1):
-
Una font d'àudio fixa produeix ones de so a una freqüència constant fe, i els fronts d'ona es propaguen de forma simètrica allunyant-se de la font a una velocitat constant c. La distància entre els fronts d'ona és la longitud d'ona. Tots els observadors escoltaran la mateixa freqüència, que serà igual a la freqüència real de la font, on fr = fe
-
La mateixa font de so està irradiant ones de so a una freqüència constant en el mateix mitjà. No obstant això, ara la font de so es mou amb una velocitat de ve = 0.7 c (Mach 0,7). Ja que la font està en moviment, el centre de cada nou front d'ona està lleugerament desplaçat a la dreta. Com a resultat, els fronts d'ones comencen a «acumular-se» al costat dret (al davant) i queden més distanciats a la banda esquerra (al darrere) de la font. Un observador situat al davant de la font escoltarà una freqüència més alta:
fr = c + 0c - 0.7c fe = 3.33 fe
i un observador situat al darrere de la font escoltarà una freqüència més baixa:
fr = c - 0c + 0.7c fe = 0.59 fe. -
Ara la font s'està movent a la velocitat del so en el medi (ve = c, (és a dir, a Mach 1). Els fronts d'ona davant de la font estan ara tots acumulats en el mateix punt. Com a resultat, un observador situat al davant de la font no detectarà res fins que la font arribi a la seva posició
f = c + 0c - c f0 = ∞
i un observador situat al darrere de la font escoltarà una freqüència més baixa
fr = c - 0c + c fe = 0.5 fe -
La font de so ja ha superat la velocitat del so en el medi, i en aquest exemple es desplaça a 1,4 c (Mach 1.4). Ja que la font s'està movent més ràpid que les ones de so que crea, el que realment fa és dirigir el front d'ones a mesura que avança. La font de so passarà davant un observador en repòs abans que l'observador senti el so. Com a resultat, un observador situat al davant de la font de percebrà:
fr = c + 0c - 1.4c fe = -2.5 fe
i un observador situat al darrere de la font escoltarà una freqüència més baixa:
fr = c - 0c + 1.4c fe = 0.42 fe.
La trajectòria de l'emissor no incident en el receptor
[modifica]En el cas de la sirena d'un vehicle d'emergència en moviment que passa prop d'un observador, començarà a sentir-se amb una freqüència més alta que la del seu to estacionari. Anirà baixant a mesura que s'acosti, i continuarà reduint-se (per sota del seu to estacionari) a mesura que s'allunyi de l'observador. L'astrònom John Dobson va explicar l'efecte d'aquesta manera: «La raó per la qual es percep com llisca gradualment el to de la sirena és perquè no atropella l'observador.»
En altres paraules, si la sirena s'acostés a l'observador directament (amb velocitat constant), la freqüència percebuda romandria invariable fins que el vehicle ho arribés a l'observador, per saltar immediatament a un nou to més baix quant comencés a allunyar-se. A causa que el vehicle no passa pel punt exacte que ocupa l'observador, sinó que el sobrepassa a certa distància, la seva velocitat relativa presenta una component radial que no es manté constant, sinó que varia com una funció de l'angle entre la seva línia de visió i la velocitat del vehicle que porta la sirena:
on és l'angle entre la velocitat d'avanç de l'objecte i la línia de visió des de l'objecte cap a l'observador.
Efectes
[modifica]Observador apropant-se a una font en repòs
[modifica]Imaginem que un observador (receptor, r) es mou a una velocitat i que té una direcció i sentit cap a una font de so (emisor, e) que es troba en repòs.[9] El medi és aire i també es troba en repòs. La font emet un so de velocitat , freqüència i longitud d'ona . Per tant, la velocitat de les ones respecte de l'observador no serà , sinó la següent:
No obstant això, com la velocitat del medi no canvia, la longitud d'ona serà la mateixa, per tant, si:
Però com esmentem en la primera explicació, l'observador a l'apropar-se a la font escoltarà un so més agut, això implica que la seva freqüència és més gran. A aquesta freqüència major captada per l'observador s'anomena «freqüència aparent», que la denominem .
L'observador escoltarà un so de major freqüència a causa que
Observador allunyant-se d'una font en repòs
[modifica]Analitzem el cas contrari. Quan l'observador s'allunya de la font, la velocitat serà i de manera anàloga podem deduir que
Font apropant-se a l'observador en repòs
[modifica]En aquest cas, la freqüència aparent percebuda per l'observador serà més gran que la freqüència real emesa per la font, el que genera que l'observador percebi un so més agut. Per tant, la longitud d'ona percebuda per a una font que es mou amb una velocitat és:
Com podem deduir que:
Font allunyant-se de l'observador en repòs
[modifica]Fent un raonament anàleg pel cas contrari (font allunyant-se), podem concloure que la freqüència percebuda per un observador en repòs amb una font en moviment serà:
Quan la font s'apropi a l'observador es posarà un signe negatiu (-) en el denominador, i quan la font s'allunyi es reemplaçarà per un signe positiu (+).
Font i observador en moviment
[modifica]Si la font i l'observador es mouen al mateix temps s'aplica la següent fórmula, que no és més que una combinació de les dues fórmules anteriors:
El sentit del desplaçament de la font i l'observador són inversos:
- Si l'observador (receptor) s'apropa a la font el numerador és positiu, si s'allunya negatiu.
- Si la font (emisor) de so s'apropa a l'observador el denominador és negatiu, si s'allunya és positiu.
- Es pot donar el cas numerador i denominador siguin una suma, i també de numerador i denominador siguin una resta.
Exemple
[modifica]Un observador es mou a una velocitat de cap a un trompetista en repòs. El trompetista està tocant (emetent) la nota la (440 Hz). Quina freqüència percebrà l'observador, sabent que la velocitat del so és ?Solució: Si l'observador s'apropa cap a la font, implica que la velocitat amb què percebrà cada front d'ona serà més gran, per tant la freqüència aparent serà major a la real (en repòs). Perquè això passi hem d'aplicar el signe (+) en l'equació.
En aquest cas particular, el trompetista emet la nota la a 440 Hz; però, l'observador percep una nota que vibra a una freqüència de 494,353 Hz, que s'aproxima altament a la freqüència pertanyent a la nota si. Musicalment parlant, l'observador percep el so amb un to més agut de què s'emet realment.
Formulació matemàtica
[modifica]Efecte Doppler galileà
[modifica]Suposem que l'emissor i el receptor es mouen sobre la mateixa línia. Hi ha tres referències galileanes a considerar:
- El sistema de referència del medi en què es propaga l'ona (per exemple l'atmosfera per a una ona sonora). Es denota per la velocitat de l’ona en aquest marc de referència (no és necessàriament la velocitat de la llum).
- El sistema de referència vinculat a l'emissor (font); anomenem la velocitat algebraica de l'emissor (font) respecte al marc de referència (1).
- El sistema de referència vinculat al receptor (observador); anomenem la velocitat del receptor respecte al marc de referència (1).
Per convenció, les velocitats es comptaran com a positives (+) en funció de la direcció i del sentit de propagació del senyal (des de l'emisor fins al receptor). Així, una velocitat positiva i negativa corresponen a un apropament entre la font i l'observador, mentre que la velocitat negativa i positiva correspondran a un distanciament.
Si és la freqüència de l'ona en el sistema de referència de l'emisor, el receptor rebrà una ona de freqüència
De fet, suposem que la font emet xiulets a una freqüència i que el moviment relatiu entre emissor i receptor es produeix al llarg de la línia que els uneix. Quan se sent el segon xiulet, el primer xiulet ha recorregut una distància
respecte al sistema de referència (1), amb . L'emisor s'ha traslladat una distància de durant el temps ; la distància que separa els dos xiulets és
Calculem el temps que separa la detecció dels dos xiulets pel receptor. Aquest últim rep el primer xiulet. Al final d’aquest temps , el receptor ha recorregut la distància de quan escolta el segon xiulet. Durant aquest temps , el segon xiulet haurà recorregut la distància
cosa que dona:
Si només l'emisor és mòbil en relació amb el sistema de referència del receptor (), llavors:
Si només el receptor és mòbil en relació amb el sistema de referència de l'emisor (), llavors:
Les dues situacions no són simètriques: de fet, si el receptor s'allunya del transmissor a una velocitat superior a , mai rebrà una ona, mentre que si el transmissor s'allunya d’un receptor estacionari, aquest rebrà sempre una ona. No es pot revertir el paper de l'emissor i receptor. En el cas clàssic, hi ha una asimetria en el desplaçament de freqüència en funció de si l'emissor o el receptor es mou (les freqüències rebudes difereixen en termes del segon ordre per a la mateixa freqüència de transmissió). Aquesta asimetria es deu a la presència del medi en què es propaguen les ones, justificada per a ones sonores.
Efecte Doppler i la relativitat galileana
[modifica]Es pot verificar que la fórmula:
resulta directament de la relativitat galileana de les longituds (aquí la longitud d'ona) que s'escriu anotant respectivament i el període i la longitud d'ona en el sistema de referència del medi de propagació en repòs:
.
La longitud d'ona, que és la mateixa als tres sistemes de referència, només depèn de la velocitat de la font respecte al sistema de referència:
.
Càlcul relativista simple
[modifica]En el cas d'ones electromagnètiques en un buit, la velocitat de l’ona és la velocitat de la llum, i no depèn del sistema de referència. A continuació, hem de tractar el problema en el marc de la relativitat especial i esperem trobar un efecte perfectament simètric ja que no podem distingir entre la velocitat del transmissor i la velocitat del receptor, només comptant la velocitat relativa entre ells.
Tanmateix, en el cas d'ones electromagnètiques en un medi dielèctric, la velocitat de l’ona depèn de la naturalesa del medi (i en particular del seu índex de refracció) i del sistema de referència (combinació de la velocitat de l’ona en el medi dielèctric i la velocitat del medi dielèctric en el sistema de referència considerat) com mostra l'experiment de Fizeau.
Abans de donar la fórmula per a l'efecte Doppler relativista en el cas general, aquí hi ha primer una demostració ràpida i simplificada de la fórmula relativista en el cas en què tots els moviments es realitzen al llarg del mateix eix, al llarg del qual és propaga el senyal. El principi del càlcul consisteix a tenir en compte l'efecte de la dilatació del temps que acompanya el pas d'un punt de referència en repòs a un punt de referència en moviment.
Canviem la notació abans de passar a una simetriació del problema. La velocitat entre l'emissor i el receptor es denotarà i es comptabilitzarà com a positiva (+) si correspon a una velocitat de distància. Aquesta és la convenció generalment adoptada en astronomia per a la velocitat radial. Per tant, si només es mou l'emissor, la seva velocitat en les fórmules anteriors és ; i si el receptor es mou sol, la seva velocitat és
- Considerem primer que és la font que es mou. Si ho calculéssim mitjançant la fórmula clàssica anterior, la freqüència del senyal a la recepció seria
- amb
Si ara tenim en compte el factor de dilatació del temps de la relativitat especial
que augmenta els temps mesurats pel receptor fix, la freqüència observada disminuirà pel factor invers de manera que la freqüència es converteix en
- Ara considerem que és el receptor que es mou. Amb la fórmula galileana tindríem
Com abans, hem de tenir en compte el factor relativista . Aquí és el receptor que es troba en moviment i la font fixa. Aquesta és l'expressió de que s'ha de multiplicar per . Per tant, obtenim la mateixa fórmula que abans:
cosa que demostra que l'efecte Doppler és perfectament simètric i depèn només de la velocitat relativa entre l'emissor i el receptor.
Aquesta simetria va ser explotada pel físic Hermann Bondi amb finalitats educatives, en el seu mètode per calcular mitjançant el factor k (k-càlcul de Bondi), representat gràficament pel diagrama de Bondi.
L'efecte Doppler relativista combina dos efectes, l'efecte galileà i l'efecte de la dilatació del temps. El primer implica la velocitat radial entre la font i l'observador, el segon el valor de la velocitat total.
Si tenim en compte el cas més clàssic d’un pla monocromàtic d'ona electromagnètica progressiva que es mou en al llarg de l'eix X amb un camp elèctric al llarg de l'eix Y
i un camp magnètic
i si considerem un marc de referència desplaçat per una velocitat respecte a tal com tenim:
llavors:
- i
d'on
s'obté un nou vector d'ones i una nova pulsació
El tensor de Maxwell permet trobar les transformacions d' , tal com passa en
- de la mateixa manera per a
La nova ona en
es pot trobar la proporcionalitat entre l’augment d’energia i l’augment de freqüència integrant la densitat d’energia respecte al volum , és a dir, si és l'energia de l’ona en i en , llavors
Efecte Doppler transversal
[modifica]L'efecte Doppler relativista tenint en compte diferents direccions de moviment és descrit per la fórmula:
on és l'angle entre la direcció del moviment de la font i la línia recta que connecta la font al receptor.
Quan la font es desplaça perpendicularment a la línia recta que connecta el receptor a la font ( = 90°), no canvia la seva distància respecte del receptor, malgrat això el receptor rep una ona amb una freqüència diferent de la transmesa:
Aquest fenomen s'anomena «efecte Doppler transversal».
Efecte Doppler-Fizeau relativista
[modifica]En la relativitat restringida, un fotó es caracteritza completament pel seu quadrivector energia-moment . Aquesta quantitat es defineix independentment de qualsevol sistema de coordenades, però és útil quan es vol fer mesures o càlculs algebraics per especificar el valor dels components d’aquest quadrivector. Si, en un sistema de coordenades, la freqüència de fotó és i el vector unitari al llarg del camí del fotó és el vector tridimensional , el quadrivector és
on és la constant de Planck
Considerem una estrella de la qual rebem a la Terra els seu fotons. Triem un sistema de coordenades terrestres OXYZ de tal manera que l'eix OX estigui orientat al llarg de la velocitat de l'estrella. La relativitat especial ens ensenya que els components d’un quadrivector en el sistema de referència en moviment de l'estrella es transformen els components en la referència terrestre segons les fórmules de Lorentz següents
amb sempre
- i
Utilitzant les notacions dels paràgrafs anteriors, les freqüències de fotons són en el sistema de referències terrestres i en el sistema de referències de l'estrella emissora. Les equacions de Lorentz després donen (els components del quadrivector són proporcionals a la freqüència i el factor comú de proporcionalitat desapareix):
on és l’angle que el fotó fa amb l'eix OX en el sistema de referència de l'estrella. Si la quantitat correspon al component radial de la velocitat relativa entre emissor i receptor en el sistema de referències de l'estrella, és a dir
podem escriure la fórmula relativista de Doppler en la forma
que dona les fórmules presentades anteriorment quan fem .
L'efecte relativista és en certa manera la combinació de l'efecte Doppler clàssic degut a la velocitat radial i al fenomen de la dilatació del temps inherents a la relativitat especial.
Anem a trobar l’angle què fa el raig de llum amb l'eix OX al sistema de referències terrestre. La diferència entre les direccions del fotó en el sistema de referències de la Terra i el sistema de referències de l'estrella és el fenomen d'aberració de la llum. De les equacions de Lorentz escrites anteriorment, tenim:
Aquestes fórmules donen una descripció relativista completa de l'efecte Doppler-Fizeau.
Hi ha una subtilesa a comprendre en el fenomen de l’aberració. Si el fotó es propaga radialment en un marc, també es propagarà en l'altre. En altres paraules, si llavors . D'altra banda, si la velocitat és perpendicular a la direcció del fotó en un sistema de referències, no serà tan estrictament en l'altre. De fet, si llavors . I si llavors .
Aplicacions
[modifica]Astronomia
[modifica]L'efecte Doppler sobre les ones electromagnètiques com la llum és de gran utilitat en astronomia, i es manifesta en els anomenats desplaçament cap al roig i desplaçament cap al blau. S'ha utilitzat per a mesurar la velocitat a la qual estrelles i galàxies estan apropant-se (com la Galàxia d'Andròmeda) o allunyant-se de la Terra; és a dir, les seves velocitats radials. Aquest fenomen físic s'utilitza per detectar estrelles binàries, per mesurar la velocitat de gir de les estrelles i galàxies, o per detectar exoplanetes.[10]
Cal tenir en compte que el desplaçament cap al roig també s'utilitza per mesurar l'expansió de l'univers, encara que en aquest cas no es tracta realment d'un efecte Doppler.[11] Més aviat, el desplaçament cap al roig a causa de l'expansió de l’univers es coneix com a desplaáment cap al vermell cosmològic, que es pot derivar purament de la mètrica FLRW sota el formalisme de la relativitat general. Dit això, també passa que hi ha efectes Doppler detectables en escales cosmològiques, que, si no s'interpreten correctament com a origen cosmològic, condueixen a l'observació de distorsions espacials a escala vermella.[12]
-
Desplaçament cap al roig de les línies espectrals en l'espectre òptic d'un supercúmul de galàxies llunyanes (dreta), comparat amb el del Sol (esquerra)
-
Animació de la modificació de les línies espectrals procedent d'una estrella orbitada per un exoplaneta
-
Dues estrelles de mida diferent orbitant el centre de massa. El desplaçament de l'estrella A és major que l'estrella B perquè la velocitat tangencial és més alta. L’amplada de línia de l'estrella B és superior a la de l'estrella A perquè l'estrella B és més gran i lluminosa.
L'ús de l'efecte Doppler sobre la llum en astronomia depèn del coneixement que es té que els espectres de les estrelles no són homogenis. Exhibeixen línies d'absorció definides de les freqüències que estan en correspondència amb les energies requerides per excitar els electrons de diversos elements d'un nivell a un altre. L'efecte Doppler és recognoscible en el fet que els patrons coneguts de les línies d'absorció no apareixen sempre coincidint amb les freqüències que s'obtenen a partir de l'espectre d'una font de llum estacionària. Atès que la llum blava té una freqüència més alta que la llum vermella, les línies espectrals d'una font de llum astronòmica que s'apropa exhibeixen un desplaçament cap al blau, i les d'un que s'allunya experimenten un desplaçament cap al roig.
Entre les estrelles més properes a la Terra, les majors velocitats radials pel que fa al Sol són +308 km / s (BD-15°4041, també coneguda com LHS 52, situada a 81,7 anys llum de distància) i -260 km / s (Woolley 9722, també coneguda com Wolf 1106 i LHS 64, situada a 78,2 anys llum de distància). Una velocitat radial positiva vol dir que l'estrella s'està allunyant de el Sol, i negativa que s'està apropant.
Radar Doppler
[modifica]L'efecte Doppler s'utilitza en alguns tipus de radar per mesurar la velocitat dels objectes detectats. Un feix de radar es dispara contra un objecte mòbil (per exemple, un automòbil, com en l'ús que fa la policia del radar Doppler per detectar la velocitat dels vehicles) a mesura que s'acosta o s'allunya de la font de radar. Cada ona successiva de radar ha de viatjar més lluny per a arribar fins al cotxe abans de ser reflectida i detectada de nou prop per la font. Com cada ona s'ha de moure més lluny, la distància entre cada ona augmenta, produint un augment de la longitud d'ona. En algunes situacions, el feix de radar s'utilitza amb el cotxe en moviment i, si s'acosta al vehicle observat, llavors cada ona successiva recorre una distància menor, produint una disminució de la longitud d'ona. En qualsevol d'aquestes situacions, els càlculs de l'efecte Doppler permeten determinar amb precisió la velocitat del vehicle amb el radar.
Per tant, el radar es pot adaptar per aprofitar aquest efecte per a:
- Radar de control de velocitat: es pot utilitzar el radar per determinar la velocitat dels automòbils. Per fer això s'utilitza un radar que emet amb una freqüència perfectament coneguda. La mesura de la freqüència de l'eco dona la velocitat del vehicle. La tecnologia moderna permet disposar de radars automàtics i binocles làser.
- Radar meteorològic: No utilitza la variació de la freqüència per l'efecte Doppler perquè és massa petita, sinó la variació de la fase entre dos polsos que tornen de la precipitació. Es tracta d’un efecte Doppler de segon ordre.
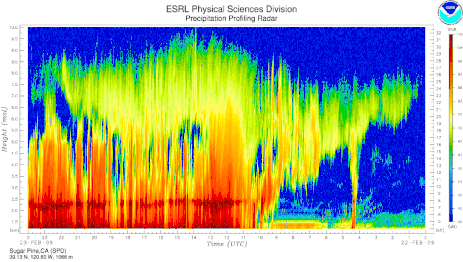
- Perfilador de vents: és un radar meteorològic que apunta verticalment i mesura la velocitat de caiguda i el desplaçament horitzontal de les precipitacions.
- Radar de mesurament balístic: moltes mesures balístiques es realitzen mitjançant el radar Doppler. Permet mesurar la velocitat del projectil, i especialment la mesura de la (velocitat inicial del projectil a la sortida de la boca del canó), la velocitat d'impacte (per exemple, per a l'elaboració d'armilles antibales), la velocitat de rotació del projectil, així com la seva trajectòria i el seu coeficient d'arrossegament.
-
Radar de control de velocitat, una de les aplicacions del radar Doppler
-
Radar meteorològic protegit per un radom
-
Reflectivitats observades per un perfilador de vents.
-
Sistema de navegació amb radar Doppler d'un avió
D'altra banda, l'espoleta de proximitat, desenvolupada durant la Segona Guerra Mundial, es basa en el radar Doppler per detonar explosius en el moment adequat en funció de la seva altura sobre el sòl o la seva distància a l'objectiu.[13]
A causa que el desplaçament Doppler afecta l'ona incident en l'objectiu, així com a l'ona reflectida de nou al radar, el canvi en la freqüència observat per un radar en moviment respecte a un objectiu també en moviment és funció de la seva velocitat relativa , i és el doble de què es registraria directament entre l'emissor i el receptor:
- .[14]
Imatges mèdiques i el mesurament del flux sanguini
[modifica]Una ecocardiografia pot, dins de certs límits, produir una avaluació precisa de la direcció del flux sanguini, de la velocitat de la sang i del teixit cardíac en qualsevol punt arbitrari usant l'efecte Doppler. Una de les limitacions és que el feix d'ultrasons ha de ser tan paral·lel possible a la direcció del flux de la sang. Els mesuraments de velocitat permeten l'avaluació de les àrees de les vàlvules cardíaques i del seu funcionament, de totes les possibles comunicacions anormals entre el costat esquerre i el dret de cor, de qualsevol fuita de sang a través de les vàlvules (insuficiència valvular), i el càlcul del cabal cardíac.
-
Ecografia Doppler en color d'el flux sanguini en una artèria caròtide; escàner i pantalla
-
Eco-Doppler: valorant el flux sanguini a través de la vàlvula mitral
-
Ultrasò Doppler d'un cor amb endocarditis
Encara que el terme «Doppler» s'ha convertit en un sinònim de «mesurament de la velocitat» a la imatge mèdica, en molts casos, no és el desplaçament de freqüència (efecte Doppler) del senyal rebut el que es mesura, sinó el canvi de fase (és a dir, quan arriba el senyal rebut, el que permet calcular distàncies).
Els mesuraments de la velocitat del flux de la sang també s'utilitzen en altres camps de la medicina ecogràfica, com obstetrícia i en neurologia. El mesurament de la velocitat del flux sanguini a les artèries i les venes basada en l'efecte Doppler és una eina eficaç per al diagnòstic de problemes vasculars com l'estenosi.[15]
Mesura de velocitat de flux
[modifica]Instruments com el velocímetre làser Doppler (LDV en anglès), i el velocímetre acústic Doppler (ADV en anglès) s'han desenvolupat per mesurar velocitats en el flux d'un fluid. El LDV emet un feix de llum i el ADV emet un tren d'ones acústiques ultrasòniques, i mesurant l'efecte Doppler en les longituds d'ona dels reflexos de les partícules que es mouen amb el flux del fluid. El flux real es calcula com una funció de la velocitat del líquid i de la fase sòlida. Aquesta tècnica permet realitzar mesuraments no invasius de cabal, amb alta precisió i amb alta freqüència.
Mesura de perfils de velocitat
[modifica]Originalment desenvolupat per a mesuraments de velocitat en aplicacions mèdiques (flux sanguini), la velocimetria d'ultrasons Doppler (UDV) permet mesurar pràcticament en temps real el perfil complet de velocitat en gairebé qualsevol fluid que contingui partícules en suspensió, com la pols, les bombolles de gas, o les emulsions. Els fluxos poden ser polsants, oscil·lants, laminars o turbulents, estacionaris o transitoris. Aquesta tècnica és completament no invasiva.
Comunicacions per satèl·lit
[modifica]Els satèl·lits es mouen molt ràpidament i poden tenir un desplaçament Doppler de desenes de Khz respecte a una estació terrestre. La velocitat dels satèl·lits, de la qual depèn la magnitud de l'efecte Doppler, sofreix canvis a causa de la curvatura de la Terra. Per evitar aquest problema s'ha ideat la compensació Doppler dinàmica, mitjançant la qual es modifica la freqüència del senyal diverses vegades durant la transmissió, de manera que el satèl·lit rebi un senyal de freqüència constant.[16]
-
Geometria per l'efecte Doppler. Variables: és la velocitat de l'estació mòbil, és la velocitat del satèl·lit, és la velocitat relativa del satèl·lit, és l'angle d'elevació del satèl·lit i és la direcció de conducció respecte al satèl·lit
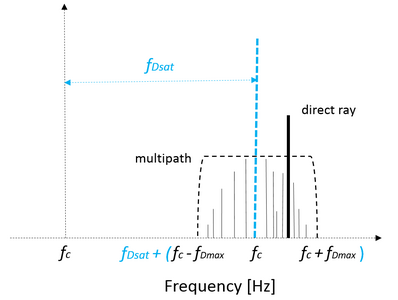
-
Efecte Doppler al canal mòbil. Variables: és la freqüència de l'ona portadora, és el desplaçament màxim Doppler a causa de l'estació mòbil en moviment (vegeu Fàding de Rayleigh) i és el canvi addicional Doppler a causa del moviment del satèl·lit.
El desplaçament Doppler de la ruta directa es pot estimar mitjançant la següent fórmula:[18]
on és la velocitat de l'estació mòbil, és la longitud de l'ona portadora, és l'angle d'elevació del satèl·lit, i és la direcció de conducció respecte al satèl·lit.
L'efecte Doppler addicional a causa del moviment del satèl·lit es pot descriure com:
on és la velocitat relativa del satèl·lit.
Quan es va planificar la missió espacial Cassini-Huygens (2005), no es va considerar l'efecte Doppler en la transmissió de dades entre el mòdul de descens Huygens i la sonda Cassini. Les proves de simulació només es van dur a terme durant el viatge, massa tard per corregir la causa, un bucle de bloqueig de fase massa rígidament parametrizat. Diverses mesures en l'àmbit de l'error van reduir la pèrdua de dades esperada del 90% al 50%. A més, es va canviar la ruta del vol de la missió (apropant el mòdul de descens Huygens a Tità de manera que les seves transmissions viatjaven perpendicularment a la seva direcció del moviment respecte a la sonda Cassini) per a reduir molt l'efecte Doppler i evitar pèrdues de dades a causa d’aquest error.[19]
Àudio
[modifica]L'altaveu Leslie, comunament associat amb els orgues Hammond, utilitza l'efecte Doppler mitjançant l'ús d'un motor elèctric que fa girar una botzina acústica al voltant d'un altaveu, fent rotar 360 ° l'orientació del so amb cada volta. Això es tradueix en l'oïda humana en què les freqüències fluctuen ràpidament per a cada nota del teclat.
-
Una nota tocada amb un orgue Hammond, mentre que el music va canviant gradualment de «chorale» a «tremolo» i viceversa en un altaveu Leslie
Mesura de vibracions
[modifica]Un vibròmetre làser Doppler (LDV) és un mètode mitjançant el qual es pot obtenir el mesurament de vibracions sense necessitat de contacte. El feix làser es dirigeix a la superfície a examinar des del LDV, i l'amplitud de la vibració i la seva freqüència s'extreuen a partir del desplaçament Doppler de la freqüència del feix làser causa del moviment de la superfície.
Robòtica
[modifica]Sovint s'utilitza l'efecte Doppler en robòtica per a la planificació de rutes dinàmiques en temps real per ajudar el moviment dels robots en un entorn sofisticat amb obstacles en moviment.[20] Aquestes aplicacions s'utilitzen especialment per a la robòtica competitiva on l'entorn està constantment canviant, com el RoboCup.
-
Partit de futbol de la lliga de robots de mida mitjana de RoboCupSoccer. RoboCup 2009
-
Robot movent-se entre obstacles en la competició RoboCupRescue. RoboCup 2009
Biologia del desenvolupament
[modifica]Durant la segmentació dels embrions dels vertebrats, el procés d'expressió genètica produeix una sèrie d'ones d'escombrat a través del mesoderma presomític, el teixit de què es formen els precursors dels vertebrats (somites). Un nou somita es forma a l'arribada d'una ona al final de l'anterior del mesoderma presomític. En el peix zebra, s'ha demostrat que l'escurçament del mesoderma presomític durant la segmentació produeix un efecte Doppler que a través de les ones orienta els moviments del teixit de l'extrem anterior. Aquest efecte Doppler contribueix al control del període de segmentació.[21]
Efecte Doppler invers
[modifica]Des de 1968, científics com Victor Veselago han especulat sobre la possibilitat d'un efecte Doppler invers. L'experiment que va afirmar haver detectat aquest efecte va ser dut a terme per Nigel Seddon i Trevor Bearpark a Bristol (Regne Unit) el 2003.[22]
Els investigadors de moltes universitats, com la Universitat de Tecnologia de Swinburne (Austràlia) i la Universitat per a Ciència i Tecnologia de Xangai (上海理工大学) (Xina), van mostrar que aquest efecte també es pot observar en freqüències òptiques. Això va ser possible gràcies a la generació d'un cristall fotònic sobre el qual projectar un raig làser. Això va fer que el vidre es comportés com un superprisma i es poguès observar l'efecte Doppler invers.[23]
Referències
[modifica]- ↑ 1,0 1,1 «Efecte Doppler». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ 2,0 2,1 Giordano, Nicholas. College Physics: Reasoning and Relationships (en anglès). Cengage Learning, 2009, p. 421–424. ISBN 978-0534424718.
- ↑ Tom, Henderson. «The Doppler Effect – Lesson 3, Waves» (en anglès). The Physics Classroom, 2017.
- ↑ Eden, Alec. The search for Christian Doppler (en anglès). Viena: Springer-Verlag, 1992. ISBN 0-387-82367-0.
- ↑ Scott Russell, John «On certain effects produced on sound by the rapid motion of the observer» (en anglès). Report of the Eighteenth Meeting of the British Association for the Advancement of Science. John Murray, Londres (1849), 18(7), 1848, pàg. 37-38.
- ↑ Houdas, Y «Doppler, Buys-Ballot, Fizeau. Historical note on the discovery of the Doppler's effect» (en anglès). Annales de cardiologie et d'angéiologie, 40(4), 4-1991, pàg. 209-213. PMID: 2053764.
- ↑ 7,0 7,1 Rosen, Joe; Gothard, Lisa Quinn. Encyclopedia of Physical Science (en anglès). Infobase Publishing, 2009, p. 155. ISBN 0-8160-7011-3.
- ↑ Strutt (Lord Rayleigh), John William. The Theory of Sound (en anglès). 2. MacMillan & Co, 1896, p. 154.
- ↑ «Doppler Effect Equation» (en anglès). TutorVista. Arxivat de l'original el 2020-07-28. [Consulta: 29 juliol 2020].
- ↑ «Doppler Shift» (en anglès). astro.ucla.edu.
- ↑ La distinció queda clara en Harrison, Edward Robert. Cosmology: The Science of the Universe (en anglès). Cambridge University Press, 2000, p. 306ff. ISBN 978-0-521-66148-5.
- ↑ Es fa una excel·lent revisió del tema en detall en Percival, Will; Samushia, Lado; Ross, Ashley; Shapiro, Charles; Raccanelli, Alvise «Review article: Redshift-space distortions» (en anglès). Philosophical Transactions of the Royal Society, 369(1957), 2011, pàg. 5058–5067. Bibcode: 2011RSPTA.369.5058P. DOI: 10.1098/rsta.2011.0370. PMID: 22084293.
- ↑ Brennen, James W «The Proximity Fuze Whose Brainchild?» (en anglès). United States Naval Institute Proceedings, 9-1968.
- ↑ http://www.radartutorial.eu/11.coherent/co06.en.html
- ↑ Evans, D. H; McDicken, W. N. Doppler Ultrasound (en anglès). Nova York: John Wiley and Sons, 2000. ISBN 0-471-97001-8.
- ↑ Qingchong, Liu «Doppler measurement and compensation in mobile satellite communications systems» (en anglès). Military Communications Conference Proceedings / MILCOM, 1, 1999, pàg. 316-320. DOI: 10.1109/milcom.1999.822695.
- ↑ Popescuy, Otilia; Harrisz, Jason S; Popescuz, Dimitrie C «Designing the Communication Sub-System for Nanosatellite CubeSat Missions: Operational and Implementation Perspectives» (en anglès). IEEE Spectrum, 2016.
- ↑ Arndt, D «On Channel Modelling for Land Mobile Satellite Reception» (en anglès). Tesi doctoral, 2015.
- ↑ Oberg, James «Titan Calling. How a Swedish engineer saved a once-in-a-lifetime mission to Saturn's mysterious moon» (en anglès). IEEE Spectrum, 04-10-2004. Arxivat de l'original el 2004-10-10 [Consulta: 29 juliol 2020].
- ↑ Agarwal, Saurabh; Gaurav, Ashish Kumar; Nirala, Mehul Kumar; Sinha, Sayan. «Potential and Sampling Based RRT Star for Real-Time Dynamic Motion Planning Accounting for Momentum in Cost Function». A: Neural Information Processing (en anglès). 11307, 2018, p. 209–221 (Lecture Notes in Computer Science). DOI 10.1007/978-3-030-04239-4_19. ISBN 978-3-030-04238-7.
- ↑ Soroldoni, D; Jörg, D. J; Morelli, L. G; Richmond, D. L; et al. «A Doppler Effect in Embryonic Pattern Formation» (en anglès). Science, 345, 2014, pàg. 222–225. Bibcode: 2014Sci...345..222S. DOI: 10.1126/science.1253089. PMID: 25013078.
- ↑ Kozyrev, Alexander B; van der Weide, Daniel W «Explanation of the Inverse Doppler Effect Observed in Nonlinear Transmission Lines» (en anglès). Physical Review Letters, 94(20), 2005, pàg. 203902. Bibcode: 2005PhRvL..94t3902K. DOI: 10.1103/PhysRevLett.94.203902. PMID: 16090248.
- ↑ «Scientists reverse Doppler Effect» (en anglès). Physical Review Letters, 07-03-2011.






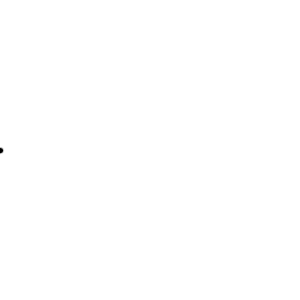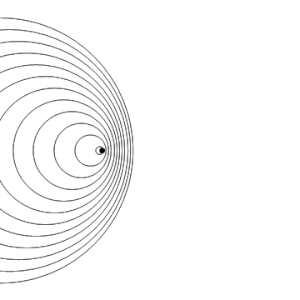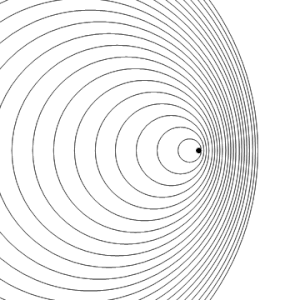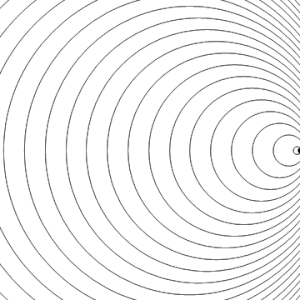











































































![{\displaystyle [1-(v^{2}/c^{2})]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b68bae23b669c269cbe23d6d53ee6468c088c0)



































































![Possibles desplaçaments Doppler en funció de l’angle d’elevació (LEO: altitud de l’òrbita '"`UNIQ--postMath-000000A1-QINU`"' = 750 km). Estació de terra fixa.[17]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a6/SatDoppler.png/401px-SatDoppler.png)