Electró-volt
| Tipus | unitat d'energia, unitat no SI acceptada pel SI, unitat derivada en UCUM, unitat de massa, constant física i unitats que no formen part del SI però s'hi mencionen i accepten |
|---|---|
| Unitat de | energia |
| Epònim | electró |
| Conversions d'unitats | |
| A unitats del SI | 0 J |
Un electró-volt (símbol: eV) —de vegades electronvolt, que també és correcte[1]— és la quantitat d'energia adquirida per un electró lliure en travessar un camp elèctric amb una diferència de potencial d'un volt. És una unitat d'energia, la qual equivalència exacta en joules és:[2]
L'energia que adquireix un electró dins d'un camp elèctric és energia cinètica , deguda a la velocitat que adquireix quan s'accelera l'electró de massa . Aquesta energia es pot calcular a partir del treball que fa el camp elèctric sobre l'electró .[3] En el cas d'un electró , el valor de la càrrega elèctrica elemental, i si la diferència de potencial és 1 volt, , resulta que l'energia cinètica és:
L'electró-volt no és una unitat del Sistema Internacional d'Unitats (SI), però està acceptada per ser utilitzada amb unitats del SI. Com que l'electró-volt és una quantitat ínfima, sovint se n'utilitzen els múltiples del SI, que són:
- El quiloelectró-volt: 1 keV = 10³ eV
- El megaelectró-volt: 1 MeV = 10⁶ eV
- El gigaelectró-volt: 1 GeV = 10⁹ eV
- El teraelectró-volt: 1 TeV = 1012 eV
Història
[modifica]L'electró-volt és una unitat d'energia introduïda en física l'octubre del 1912 amb el nom en anglès d'equivalent volt,[4] en un article sobre l'efecte fotoelèctric, pel físic anglès Owen Willans Richardson (1879-1959), Premi Nobel de Física del 1928, i l'estatunidenc Karl Taylor Compton (1887-1954) de la Universitat de Princeton, germà del Premi Nobel de Física del 1927 Arthur Holly Compton (1892-1962).[5]
Als EUA, amb el desenvolupament de la física de partícules, es va començar a utilitzar la unitat BeV (o bev o Bev), on B representava un bilió (de l'anglès "billion"). El 1948, però, la IUPAP va rebutjar-ne l'ús i va preferir l'ús del prefix gig per a mil milions d'electrovolts, per la qual cosa la unitat s'abreuja GeV.[6]
En algunes publicacions antigues, s'usa "ev" com a abreviatura d'electronvolt.[7]
El nom de l'accelerador de partícules Bevatron (en funcionament de 1954 a 1993, Berkeley, EUA) es va derivar de la unitat BeV. Segons la mateixa clau, es va nomenar l'accelerador Tevatron (1983-2011, Illinois), que accelerava protons i antiprotons a energies de fins a 1 TeV. El nom Zevatron s'usa de vegades amb exageració per a fonts astrofísiques naturals de partícules amb energies de fins a 1021 eV (prefix zetta). Mai no s'havia registrat l'energia més gran d'una sola partícula.[8]
Radiació electromagnètica
[modifica]La radiació electromagnètica a partir de l'infraroig proper fins als raigs còsmics més energètics sovint es classifiquen en intervals d'energia mesurats en electró-volts. La relació entre l'energia en joules del fotó i la freqüència de la radiació és la fórmula d'Einstein , on és la constant de Planck i la freqüència en hertz.
| Nom de la radiació | Energies (eV) | Energies (J) | Freqüències (Hz) |
|---|---|---|---|
| Part de les microones i infraroig llunyà | 0,1 – 1 | (1,6 – 16) × 10–20 | (3 – 30) × 1013 |
| Infraroig proper, visible i ultraviolat proper | 1 – 10 | (1,6 – 16) × 10–19 | (3 – 30) × 1014 |
| Ultraviolat de buit | 10 – 100 | (1,6 – 16) × 10–18 | (3 – 30) × 1015 |
| Raigs X blans | 100 – 1 000 | (1,6 – 16) × 10–17 | (3 – 30) × 1016 |
| Raigs X blans | (1 – 10) × 10³ | (1,6 – 16) × 10–16 | (3 – 30) × 1017 |
| Raigs X durs i raigs γ blans | (1 – 10) × 104 | (1,6 – 16) × 10–15 | (3 – 30) × 1018 |
| Raigs γ blans i durs | (1 – 10) × 10⁵ | (1,6 – 16) × 10–14 | (3 – 30) × 1019 |
| Raigs γ durs i raigs γ còsmics | (1 – 10) × 106 | (1,6 – 16) × 10–13 | (3 – 30) × 1020 |
| Raigs γ produïts per raigs còsmics | (1 – 10) × 107 | (1,6 – 16) × 10–12 | (3 – 30) × 1021 |
Energies de fenòmens atòmics i moleculars
[modifica]
Diferents energies de fenòmens atòmics s'expressen en electró-volts. És el cas de l'energia d'ionització, l'energia que cal aportar a un àtom o una molècula per extreure-li un electró. És una propietat característica de cada element químic i presenta una variació regular en la taula periòdica. Els valors oscil·len entre 3,89 eV pel cesi fins a 24,59 eV de l'heli. També el treball d'extracció dels metalls o funció de treball, l'energia necessària per extreure electrons d'un sòlid, s'expressen en electró-volts. S'empra en l'efecte fotoelèctric i l'efecte termoiònic.
| Elements | Al | Ag | Be | Cd | Ca | Cs | Co | Cu | Ni | Nb | Au | Pt | Zn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Funció de treball (eV) | 4,08 | 4,26-4,73 | 5,0 | 4,07 | 2,9 | 1,95 | 5,0 | 4,7 | 5,01 | 4,3 | 5,1 | 6,36 | 4,3 |
Masses en eV
[modifica]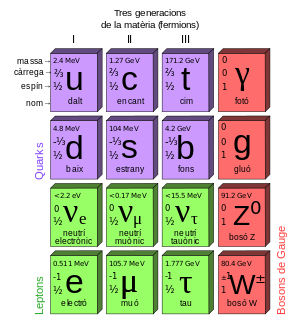
A causa de la relació massa i energia o establerta pel físic alemany Albert Einstein el 1905, en física de partícules usa l'eV/c² com a unitat de massa, amb l'avantatge que la conversió entre massa i energia és trivial. Per exemple, un electró i un positró, cadascun amb una massa de 0,511 MeV/c², poden aniquilar-se generant una energia de 2 · 0,511 MeV = 1,022 MeV. L'equivalència és:
- 1 eV/c² = 1,783 × 10–36 kg
- 1 keV/c² = 1,783 × 10–33 kg
- 1 MeV/c² = 1,783 × 10–30 kg
- 1 GeV/c² = 1,783 × 10–27 kg
Grandària de la unitat
[modifica]L'electró volt és una quantitat extremadament petita d'energia a una escala comuna. L'energia d'un mosquit volador és d'aproximadament un bilió d'electrovolts.[11] Per tant, la unitat és útil on les energies típiques són molt petites, és a dir, en un món de partícules Aquí, també, 1 eV és sovint una energia relativament petita, per la qual cosa s'utilitzen múltiples i prefixos més grans. 1 keV és mil eV, 1 MeV és un milió d'eV, 1 GeV és mil milions d'eV, 1 TeV és un bilió de eV. De vegades s'utilitza l'abreviatura com a sigla.[12]
L'accelerador de partícules més gran (LHC) subministra a cada protó 7 TeV.[13] En trencar un sol nucli d'urani 235U, s'alliberen aproximadament 215 MeV. En combinar un nucli d'un àtom de deuteri amb un nucli de triti, s'alliberen 17,6 MeV.[14] A les pantalles de televisió en color, els electrons són accelerats per un alt voltatge d'uns 32.000 volts, de manera que els electrons adquireixen una energia cinètica de 32 keV. Els electrovolts són molt adequats per mesurar l'energia dels enllaços químics, són de l'ordre d'unitats o desenes d'eV per una molècula.[14] Calen 13,6 eV per extreure un electró d'un àtom d'hidrogen (ionització).[14] L'ordre d'eV també té energies de fotons de llum visible.[14] En la termodinàmica es produeixen energies inferiors als electronvolts; per exemple, l'energia cinètica mitjana de les partícules d'aire a temperatura ambient és de 38 meV (mil·lielectrovolts).[14]
La velocitat d'un electró amb una energia cinètica d'1 eV és d'aproximadament 593 km/s. La velocitat d'un protó amb la mateixa energia cinètica és aleshores de només 13,8 km/s.
La magnitud de l'electronvolt en unitats SI es determina mesurant la càrrega de l'electró. El més precís dels mètodes coneguts és el mesurament de l'efecte Josephson, que determina el valor de la constant de Josephson . La magnitud de la càrrega elemental es determina llavors a partir de la relació . Zde . Aquí és la constant de von Klitzing, que es mesura amb més precisió que . La desviació estàndard relativa del mesurament constant de Josephson és 2,5 × 10 −8 (2,5 milionèsimes de percentatge), i la conversió d'un electró-volt en un juliol és igual de precisa.[15]
Experiments de dispersió
[modifica]En un experiment de dispersió nuclear de baixa energia, és convencional referir-se a l'energia de retrocés nuclear en unitats d'eVr, keVr, etc. Això distingeix l'energia d'entrada nuclear de l'energia d'entrada "equivalent a l'electró" (eVee, keVee, etc.) mesurada per llum de centelleig. Per exemple, el rendiment d'un fototub es mesura en phe/keVee (fotoelectrons per keV d'energia equivalent a l'electró). La relació entre eV, eVr i eVee depèn del medi en què té lloc la dispersió, i cal establir-lo empíricament per a cada material.
Relació amb altres propietats físiques i unitats
[modifica]Massa
[modifica]Per equivalència massa-energia, l'electronvoltio correspon a una unitat de massa. És comú en física de partícules, on les unitats de massa i energia sovint s'intercanvien, expressar la massa en unitats de eV/c2, on c és la velocitat de la llum en el buit (d'E = mc2). És comú expressar informalment la massa en termes d'eV com a unitat de massa, utilitzant efectivament un sistema d'unitats naturals amb c fixat en 1.[16] El quilogram equivalent de 1eV/c2 és:
Per exemple, un electró i un positró, cadascun amb una massa de 0.511 MeV/c², poden aniquilar-se per produir 1,022 MeV d'energia. Un protó té una massa de 0,938 GeV/c². En general, les masses de tots els hadrons són de l'ordre d'1 GeV/c², el que fa del GeV/c2 una unitat de massa convenient per a la física de partícules:[17]
- 1 GeV/c² = 1.78266192×10−27 kg.
La constant de massa atòmica (mu), una dotzena part de la massa d'un àtom de carboni-12 s'aproxima a la massa d'un protó. Per convertir a electronvolt massa-equivalent, es pot utilitzar la fórmula:
- mu = 1 Da = 931.4941 MeV/c² = 0.9314941 GeV/c².
Mesura de la temperatura
[modifica]En algunes àrees, com per exemple la física dels plasmes, pot ser convenient utilitzar l'electró-volt com la unitat de la temperatura. Per a saber la temperatura d'una partícula en kèlvins, a partir de la seva energia en electró-volts, es fa servir la constant de Boltzmann kB.
Per exemple, una temperatura típica del plasma a una fusió per confinament magnètic és de 15 keV, és a dir 174 MK (megakelvins). La temperatura ambient (~ 20 °C) correspondria a 1/40e electró-volt (0,025 eV).
Moment
[modifica]Amb la física d'altes energies, sovint s'utilitza l'electronvolt com a unitat de moment (quantitat de moviment). Una diferència de potencial de 1 volt causa que un electró guanyi una quantitat d'energia (o sigui 1 eV). Això dóna lloc a l'ús d'eV (i keV, MeV, GeV o TeV) com a unitats de moment, perquè l'energia proveïda resulta en l'acceleració de la partícula.
Les dimensions de les unitats de moment són L1 M1 T -1. Les dimensions d'unitats d'energia són L2 M1 T -2. Per tant, dividint les unitats d'energia (com eV) per una constant fonamental que té unitats de velocitat L1 T -1, facilita la conversió requerida dutilitzar unitats denergia per descriure moment. En el camp de la física de partícules d'alta energia, la unitat de velocitat fonamental és la velocitat de la llum al buit c.
Si es divideix l'energia en eV per la velocitat de la llum, podeu descriure el moment d'un electró en unitats de eV/c.[18][19]
La constant fonamental de velocitat c sovint és deixada de costat de les unitats de moment mitjançant definir unitats de longitud tal com el valor de c és unitari. Per exemple, si el moment p d'un electró es diu que és d'1 GeV, per tant, la conversió a MKS es realitza com:
Distància
[modifica]A física de partícules, un sistema d′"unitats naturals" en el qual la velocitat de la llum en el buit c i la constant de Planck reduïda ħ són adimensionals i iguals a la unitat és àmpliament utilitzat: c = ħ = 1. En aquestes unitats, tant distàncies com a temps són expressats en unitats d'energia inverses (mentre que energia i massa són expressats en les mateixes unitats, vegeu equivalència massa energia). En particular, les longituds de dispersió de partícules sovint són presentades en unitats de la inversa de les masses de partícules.
Fora d'aquest sistema d'unitats, els factors de conversió entre electrovolti, segon i nanòmetre són les següents:
Aquestes relacions també permeten expressar la vida mitjana τ d'una partícula inestable (en segons) en funció de la seva amplada de la ressonància Γ (en eV) mitjançant Γ = ħ/τ. Per exemple, el mesó B0 posseeix una vida mitjana de 1.530(9) picosegons, l'amplada mitjana de ressonància és cτ = 459.7 μm, o una amplada de ressonància de 4.302 10-4 eV.
En canvi, les minúscules diferències de masses dels mesons responsables de les oscil·lacions dels mesons sovint són expressades en picosegons inversos a la unitat que resulta més convenient.
L'energia expressada en electrovolts de vegades és expressada mitjançant la longitud d'ona de la llum amb fotons de la mateixa energia:
- sovint són presentades en unitats de la inversa de la massa de la partícula.
Referències
[modifica]- ↑ «Electró-volt». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ «CODATA Value: electron volt». [Consulta: 28 juliol 2023].
- ↑ Jackson, J. D.. Classical Electrodynamics. 2a ed. Nova York: John Wiley & Sons, 1975, p. 45. ISBN 978-0-471-43132-9.
- ↑ Gyllenbok, Jan. Encyclopaedia of historical metrology, weights, and measures. Cham: Birkhäuser, 2018. ISBN 978-3-319-69067-4.
- ↑ Richardson, O.W.; Compton, Karl T. «LIII. The photoelectric effect». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 24, 142, 10-1912, pàg. 575–594. DOI: 10.1080/14786441008637361. ISSN: 1941-5982.
- ↑ MADORE, Barry F. The Lexicon and Glossary of Terms in LEVEL 5, heslo Electron volt [online]. Pasadena, Kalifornie, USA: Caltech and Carnegie, 2002-08-14, rev. 2006-01-10
- ↑ National Research Council (U.S.). Conference on Glossary of Terms in Nuclear Science and Technology, National Research Council (U.S.). A glossary of terms in nuclear science and technology. New York: American Society of Mechanical Engineers, 1957
- ↑ Kulhanek, Petr. Mohou Alfvénovy vlny i za vysoké energie v kosmickém záření?. Aldebaran Bulletin. 2009-04-17, ročník 2009, číslo 16
- ↑ Lide, David R.; Frederikse, H. P. R.. CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data. 76th ed. Boca Raton: CRC press, 1997. ISBN 978-0-8493-0597-9.
- ↑ Zolotoyabko, Emil. Introduction to solid state physics for materials engineers. Weinheim: Wiley-VCH, 2021. ISBN 978-3-527-34884-8.
- ↑ LHC Glossary, heslo TeV [online]. CERN [cit. 2009-04-08]
- ↑ WAGNER, Vladimír. Jak se zkoumá narušení chirální symetrie aneb jak mi vládce podsvětí pomůže zjistit, proč má půvabná ženuška váží 64 kilo, místo méně než 1,4 kg, jak by se dalo očekávat [online]. 2001-10-25 [cit. 2009-04-14]
- ↑ LHC Machine Outreach [online]. CERN [cit. 2009-04-08]
- ↑ 14,0 14,1 14,2 14,3 14,4 NAVE, Carl. HyperPhysics [online]. Atlanta, USA: Georgia State University, Department of Physics and Astronomy, 1999 [cit. 2009-04-08]. Hesla: Energy From Uranium Fission, Deuterium-Tritium Fusion, Chemical Bonding, Hydrogen, Photon Energies for EM Spectrum, Thermal Energy.
- ↑ «CODATA Value: electron volt-joule relationship». [Consulta: 24 juny 2019].
- ↑ Barrow, J. D. «Natural Units Before Planck». Quarterly Journal of the Royal Astronomical Society, vol. 24, 1983, pàg. 24. Bibcode: 1983QJRAS..24...24B.
- ↑ Gron Tudor Jones. «ch/event/318730/contributions/737345/attachments/613347/843809/gevtypeunitshst14.pdf Unidades de energía y momento en la física de partículas» (PDF). Indico.cern.ch. [Consulta: 5 juny 2022].
- ↑ «Units in particle physics». Associate Teacher Institute Toolkit. Fermilab, 22-03-2002. Arxivat de l'original el 14 May 2011. [Consulta: 13 febrer 2011].
- ↑ «Special Relativity». Virtual Visitor Center. SLAC, 15-06-2009. Arxivat de l'original el 2008-08-28. [Consulta: 13 febrer 2011].
Bibliografia
[modifica]- Diccionari de la llengua catalana, dirigit per Jesús Giralt i Radigales, Enciclopèdia Catalana, Barcelona 2002.
- Donald H. Perkins. Introduction to High Energy Physics 4th Edition. (2000). 442 pàg. ISBN 0521621968, ISBN 978-0521621960.
- David Griffiths. Introduction to Elementary Particles 2nd Edition. (2008). 470 pàg. ISBN 9783527406012, ISBN 978-3527406012


























