Encreuament evitat

En física quàntica i química quàntica, un encreuament evitat (de vegades anomenat encreuament previst, ^[1] no encreuament o anticreuament) és el fenomen en què dos valors propis d'una matriu hermítica que representen un observable quàntic i depenent de N paràmetres reals continus no es poden igualar en valor ("creu") excepte en un col·lector de dimensions N-3. El fenomen també es coneix com el teorema de von Neumann-Wigner. En el cas d'una molècula diatòmica (amb un paràmetre, és a dir, la longitud de l'enllaç), això significa que els valors propis no es poden creuar en absolut. En el cas d'una molècula triatòmica, això vol dir que els valors propis només poden coincidir en un sol punt (vegeu intersecció cònica).^[2]

Això és especialment important en la química quàntica. En l'aproximació de Born-Oppenheimer, l'hammiltonià molecular electrònic està diagonalitzat en un conjunt de geometries moleculars diferents (els valors propis obtinguts són els valors de les superfícies d'energia potencial adiabàtica). Les geometries per a les quals les superfícies d'energia potencial eviten creuar són el lloc on falla l'aproximació de Born-Oppenheimer.^[3]

Els encreuaments evitats també es produeixen en les freqüències de ressonància dels sistemes mecànics sense amortiment, on les matrius de rigidesa i massa són simètriques reals. Allà les freqüències de ressonància són l'arrel quadrada dels valors propis generalitzats.^[4]

En sistemes de dos estats

Emergència

L'estudi d'un sistema de dos nivells és de vital importància en mecànica quàntica perquè incorpora la simplificació de molts dels sistemes físicament realitzables. L'efecte de la pertorbació en un sistema hamiltonià de dos estats es manifesta mitjançant encreuaments evitats en la trama de la corba de diferència d'energia individual vs energia dels estats propis. L'hammiltonià de dos estats es pot escriure com

$H={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}\,\!$

Els valors propis dels quals són $\textstyle E_{1}$ i $\textstyle E_{2}$ i els vectors propis, $\textstyle {\begin{pmatrix}1\\0\end{pmatrix}}$ i $\textstyle {\begin{pmatrix}0\\1\end{pmatrix}}$ . Aquests dos vectors propis designen els dos estats del sistema. Si el sistema està preparat en qualsevol dels estats, es mantindria en aquest estat. Si $\textstyle E_{1}$ passa a ser igual a $E_{2}$ hi haurà una doble degeneració en l'Hamiltonià. En aquest cas, qualsevol superposició dels estats propis degenerats és evidentment un altre estat propi de l'Hamiltonià. Per tant, el sistema preparat en qualsevol estat romandrà en aquest per sempre.

S'ha evitat l'encreuament en el sistema de dos estats. El pas de nivell d'energia s'evita amb l'augment del paràmetre $\textstyle w(=|W|)$ . En absència de pertorbació externa, els nivells haurien creuat si els estats energètics originals fossin degenerats, és a dir $\textstyle \Delta E=0$

Tanmateix, quan es sotmeten a una pertorbació externa, els elements de la matriu de l'Hamiltonià canvien. Per simplificar, considerem una pertorbació amb només elements diagonals. Com que l'hammiltonià global ha de ser hermitià, podem escriure simplement el nou hamiltonià

$H'=H+P={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}+{\begin{pmatrix}0&W\\W^{*}&0\end{pmatrix}}={\begin{pmatrix}E_{1}&W\\W^{*}&E_{2}\end{pmatrix}}\,\!$

On P és la pertorbació amb zero termes diagonals. El fet que P sigui hermitià fixa les seves components fora de la diagonal. Els estats propis modificats es poden trobar diagonalitzant l'hammiltonià modificat. Resulta que els nous valors propis són,

E_{+}={\frac {1}{2}}(E_{1}+E_{2})+{\frac {1}{2}}{\sqrt {(E_{1}-E_{2})^{2}+4|W|^{2}}}

E_{-}={\frac {1}{2}}(E_{1}+E_{2})-{\frac {1}{2}}{\sqrt {(E_{1}-E_{2})^{2}+4|W|^{2}}}

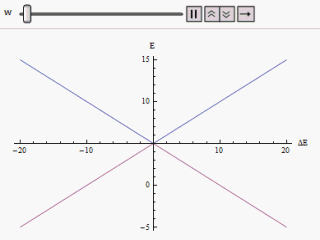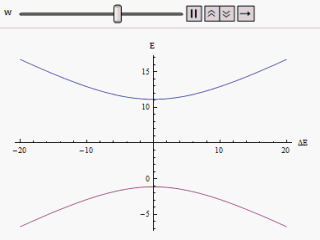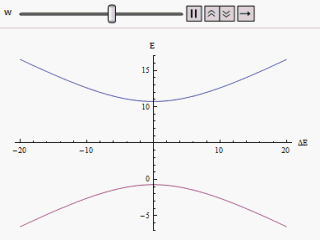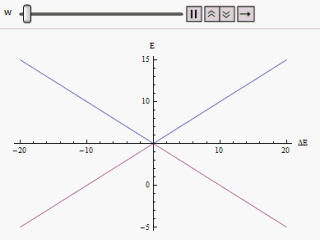
Si es dibuixa una gràfica variant $\textstyle (E_{1}-E_{2})$ al llarg de l'eix horitzontal i $\textstyle E_{+}$ o $\textstyle E_{-}$ al llarg de la vertical, trobem dues branques d'una hipèrbola (com es mostra a la figura). La corba s'aproxima asimptòticament als nivells d'energia originals impertorbables. Analitzant les corbes es fa evident que encara que els estats originals fossin degenerats (és a dir $\textstyle E_{1}=E_{2}$ ) els nous estats d'energia ja no són iguals. Tanmateix, si $\textstyle W$ s'estableix a zero que podem trobar a $\textstyle (E_{1}-E_{2})=0$ , $\textstyle E_{+}=E_{-}$ i els nivells es creuen. Així amb l'efecte de la pertorbació s'eviten aquests passos a nivell.