Equació d'Eckhaus
En física matemàtica, l'equació d’Eckhaus (o l'equació de Kundu-Eckhaus) és una equació diferencial parcial no-lineal dins la classe no-lineal de Schrödinger:[1]
L'equació va ser introduïda de forma independent per Wiktor Eckhaus i per Anjan Kundu per modelar la propagació de les ones en medis dispersius.[2][3] L'equació de Kundu-Eckhaus admet molts tipus diferents de solucions analítiques (igual que l'equació no-lineal de Schrödinge), incloent, però sense limitar-se, les solucions racionals d'onades gegants.[4] El comportament de les seves solucions estocàstiques d'onada gegant i els seus espectres es poden utilitzar amb finalitats de detecció precoç.[5]
Linealització
[modifica]L'equació d’Eckhaus es pot linealitzar a l'equació lineal de Schrödinger:[6]
mitjançant la transformació no-lineal:[7]
La transformació inversa és:
Aquesta linealització també implica que l'equació d’Eckhaus és integrable.
-
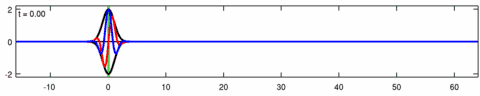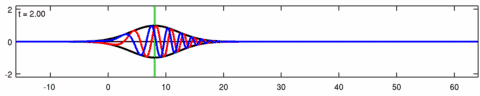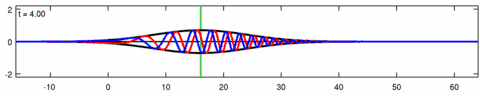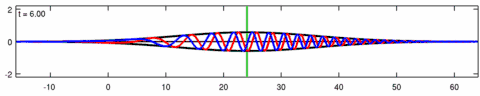
Animació d'una solució de paquets d'ones de l'equació d'Eckhaus. La línia blava és la part real de la solució, la línia vermella és la part imaginària i la línia negra és l'embolcall d’ona (valor absolut). Tingueu en compte l’asimetria del sobre per a l'equació d’Eckhaus, mentre que el sobre (de la solució corresponent a l'equació lineal de Schrödinger) és simètric (a ). Les ones curtes del paquet es propaguen més ràpidament que les ones llargues
-
Animació de la solució de paquets d’ones de l'equació lineal de Schrödinger (corresponent amb l’animació anterior per a l'equació d’Eckhaus). La línia blava és la part real de la solució, la línia vermella és la part imaginària, la línia negra és l'embolcall d’ona (valor absolut) i la línia verda és el centroide del paquet d’ona
Solució d’ones itinerants
[modifica]L'equació d’Eckhaus té diverses solucions d’ones itinerants:
Referències
[modifica]Bibliografia
[modifica]- Ablowitz, M.J.; Ahrens, C.D.; De Lillo, S. «On a "quasi" integrable discrete Eckhaus equation» (en anglès). Journal of Nonlinear Mathematical Physics, 12 (suplement 1), 2005, pàg. 1–12. Bibcode: 2005JNMP...12S...1A. DOI: 10.2991/jnmp.2005.12.s1.1.
- Calogero, F.; De Lillo, S. «The Eckhaus PDE iψt + ψxx+ 2(|ψ|²)x ψ + |ψ|4 ψ = 0» (en anglès). Inverse Problems, 3(4), 1987, pàg. 633–682. Bibcode: 1987InvPr...3..633C. DOI: 10.1088/0266-5611/3/4/012.
- Eckhaus, W. «The long-time behaviour for perturbed wave-equations and related problems» (en anglès). Department of Mathematics, University of Utrecht, 1985..
Publicat en part en: Eckhaus, W. Trends in applications of pure mathematics to mechanics (en anglès). 249. Berlin: Springer, 1986, p. 168–194 (Lecture Notes in Physics). DOI 10.1007/BFb0016391. ISBN 978-3-540-16467-8. «Contribució: The long-time behaviour for perturbed wave-equations and related problems» - Bayindir, C. «Rogue waves of the Kundu–Eckhaus equation in a chaotic wavefield» (en anglès). Physical Review E, 93(032201), 2016a. arXiv: 1601.00209. Bibcode: 2016PhRvE..93c2201B. DOI: 10.1103/PhysRevE.93.032201.
- Bayindir, C. «Rogue wave spectra of the Kundu–Eckhaus equation» (en anglès). Physical Review E, 93(062215), 2016b. arXiv: 1604.08035. Bibcode: 2016PhRvE..93f2215B. DOI: 10.1103/PhysRevE.93.062215.
- Kundu, A. «Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations» (en anglès). Journal of Mathematical Physics, 25, 1984, pàg. 3433–3438. Bibcode: 1984JMP....25.3433K. DOI: 10.1063/1.526113.
- Taghizadeh, N.; Mirzazadeh, M.; Tascan «The first-integral method applied to the Eckhaus equation» (en anglès). Applied Mathematics Letters, 25(5), 2012, pàg. 798–802. DOI: 10.1016/j.aml.2011.10.021.
- Zwillinger, D. Handbook of differential equations (en anglès). Academic Press, 1998. ISBN 9780127843964.