Estimació de la densitat de probabilitat

Demostració de l'estimació de la densitat mitjançant l'estimació de la densitat del nucli: la densitat real és una barreja de dos gaussians centrats al voltant de 0 i 3, mostrats amb una corba blava sòlida. En cada fotograma, es generen 100 mostres a partir de la distribució, mostrades en vermell. Centrat a cada mostra, es dibuixa un nucli gaussià en gris. Mitjançant les gaussianes s'obté l'estimació de la densitat que es mostra a la corba negra discontínua.

En estadística, l'estimació de la densitat de probabilitat o simplement l'estimació de la densitat és la construcció d'una estimació, basada en dades observades, d'una funció de densitat de probabilitat subjacent no observable. La funció de densitat no observable es considera com la densitat segons la qual es distribueix una gran població; les dades solen considerar-se com una mostra aleatòria d'aquesta població.

S'utilitzen una varietat d'enfocaments per a l'estimació de la densitat, incloses les finestres de Parzen i una sèrie de tècniques d'agrupació de dades, inclosa la quantificació vectorial. La forma més bàsica d'estimació de la densitat és un histograma reescalat.

Densitat estimada de p (glu | diabetis=1) (vermell), p (glu | diabetis=0) (blau) i pàg (glu) (negre)

Exemple

Considerarem els registres de la incidència de la diabetis. El següent es cita textualment de la descripció del conjunt de dades:

Una població de dones d'almenys 21 anys, d'origen indi Pima i que vivia a prop de Phoenix, Arizona, es va fer la prova de diabetis mellitus segons els criteris de l'Organització Mundial de la Salut. Les dades van ser recollides per l'Institut Nacional de Diabetis i Malalties Digestives i Renals dels EUA. Hem utilitzat els 532 registres complets.

Probabilitat estimada de p (diabetis=1 | glu)

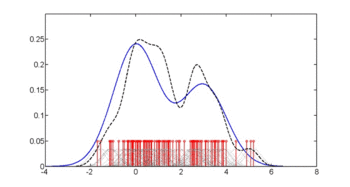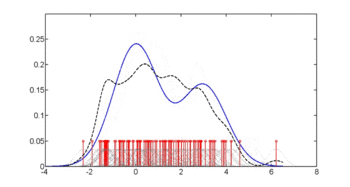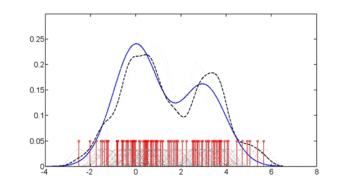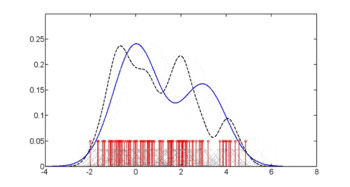
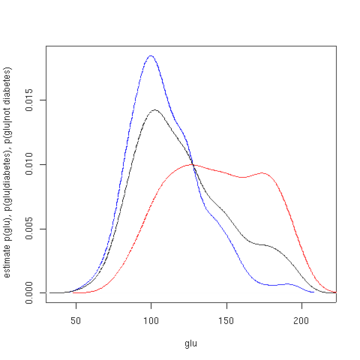
En aquest exemple, construïm tres estimacions de densitat per a "glu" (concentració de glucosa plasmàtica), una condicionada a la presència de diabetis, la segona condicionada a l'absència de diabetis i la tercera no condicionada a la diabetis. Les estimacions de densitat condicionals s'utilitzen llavors per construir la probabilitat de diabetis condicionada a "glu".

Les dades "glu" es van obtenir del paquet MASS del llenguatge de programació R.

La mitjana de "glu" en els casos de diabetis és de 143,1 i la desviació estàndard és de 31,26. La mitjana de "glu" en els casos sense diabetis és de 110,0 i la desviació estàndard és de 24,29. D'això veiem que, en aquest conjunt de dades, els casos de diabetis s'associen a nivells més elevats de "glu". Això quedarà més clar mitjançant gràfics de les funcions de densitat estimades.

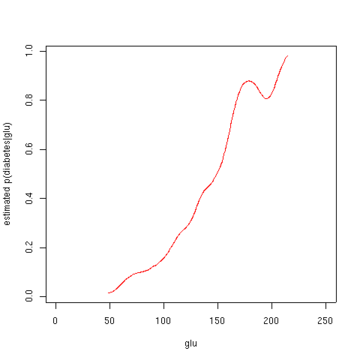
A partir de la densitat de "glu" condicionada a la diabetis, podem obtenir la probabilitat de diabetis condicionada a "glu" mitjançant la regla de Bayes. Per a la brevetat, "diabetis" s'abreuja "db". en aquesta fórmula.

$p({\mbox{diabetes}}=1|{\mbox{glu}})={\frac {p({\mbox{glu}}|{\mbox{db.}}=1)\,p({\mbox{db.}}=1)}{p({\mbox{glu}}|{\mbox{db.}}=1)\,p({\mbox{db.}}=1)+p({\mbox{glu}}|{\mbox{db.}}=0)\,p({\mbox{db.}}=0)}}$

Aplicació i finalitat

Un ús molt natural de les estimacions de densitat és en la investigació informal de les propietats d'un conjunt de dades donat. Les estimacions de densitat poden donar una indicació valuosa de característiques com ara la sessió i la multimodalitat de les dades. En alguns casos, obtindran conclusions que després es poden considerar com a certes per si mateixes, mentre que en d'altres l'únic que faran és indicar el camí per a una anàlisi posterior i/o recollida de dades.