Estructura de Weaire–Phelan
| Estructura de Weaire–Phelan | |
|---|---|

|
En geometria, l'estructura de Weaire–Phelan és una estructura tridimensional complexa que representa una escuma idealitzada constituïda per bombolles de la mateixa mida. El 1993, el físic Denis Weaire, del Trinity College de Dublín, juntament amb el seu estudiant Robert Phelan, van descobrir, en simulacions d'escumes per ordinador que aquesta estructura era una solució millor al "problema Kelvin" que la millor solució coneguda fins llavors, l'estructura Kelvin.[1]
El problema Kelvin
[modifica]
El 1887, Lord Kelvin va preguntar com es podria dividir l'espai en cel·les d'igual volum amb la mínima superfície entre elles, és a dir, quina era l'escuma de bombolles més eficient.[2] Des d'aleshores, aquest problema es coneix com a problema de Kelvin.
Va proposar una escuma, basada en l'enrajolat cúbic bitruncat, anomenada estructura Kelvin. Es tracta de l'enrajolat uniforme convex format per l'octàedre truncat, que és un poliedre de 14 cares que omple l'espai (un tetradecàedre), amb 6 cares quadrades i 8 cares hexagonals. Per adaptar-se a les lleis de Plateau, que regulen les estructures de les escumes, les cares hexagonals de la variant de Kelvin estan lleugerament corbades.
La conjectura de Kelvin és que aquesta estructura soluciona el problema de Kelvin, és a dir, que l'escuma de l'enrajolat cúbic bitruncat és la més eficient. Aquesta conjectura fou àmpliament acceptada, i no va ser superada durant més de 100 anys, fins que va ser rebatuda per la descoberta de l'estructura de Weaire–Phelan.
El 2009, Ruggero Gabbrielli[3] va publicar una manera d'utilitzar l'equació Swift–Hohenberg per trobar solucions candidates al problema Kelvin en superfícies mínimes.[4]

L'estructura de Weaire–Phelan difereix de la de Kelvin en què utilitza dues classes de cel·les, tot i que tenen un volum igual.
Des d'un punt de vista topològic i simètric, una d'elles és un piritòedre, un dodecàedre irregular amb cares pentagonals, que posseeix simetria tetraèdrica (Th).
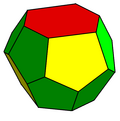
L'altra és una forma de trapezòedre hexagonal truncat, una espècie de tetradecàedre amb dues cares hexagonals i dotze pentagonals, i que en aquest cas només posseeix dos plans de mirall i una simetria de rotació impròpia.
De la mateixa manera que els hexàgons de l'estructura de Kelvin, els pentàgons en ambdós tipus de cel·les són lleugerament corbats. L'àrea de superfície de l'estructura de Weaire–Phelan és un 0,3% inferior a la de Kelvin. No s'ha demostrat, però, que l'estructura de Weaire–Phelan sigui òptima. Els experiments també han mostrat que, amb condicions de frontera favorable, les bombolles de volum igual s'autoassemblen espontàniament en una fase A15, els àtoms de la qual coincideixen amb els centroides dels poliedres de l'estructura Weaire–Phelan.[5][6]

Aproximació polièdrica
[modifica]L'enrajolat polièdric associat amb l'estructura de Weaire–Phelan (obtingut per l'aplanament de les cares i el redreçament de les arestes) també s'anomena, de manera més general, estructura de Weaire–Phelan. Ja es coneixia molt abans del descobriment de l'estructura Weaire–Phelan, però l'aplicació al problema de Kelvin va passar desapercebuda.[7]
Es troba en dos geometries relacionades d'estructura cristal·lina en química.
Allà on els components del cristall se situen als centres de cantonades dels poliedres, forma una de les fases Franc–Kasper.[8]
Allà on els components del cristall se situen a les cantonades dels poliedres, es coneix com a "estructura de clatrat de tipus I". Els hidrats de gas formats per metà, propà i diòxid de carboni a temperatures baixes tenen una estructura en què les molècules d'aigua se situen als nodes de l'estructura Weaire–Phelani i interactuen mitjançant enllaços d'hidrogen, i les molècules de gas més grans queden atrapades en les gàbies polièdriques. Alguns metalls alcalins silicurs i germànids també formen aquesta estructura (Si/Ge als nodes, metalls alcalins a les gàbies), com ho fa també la melanoflogita (silici als nodes, enllaçat amb oxigen al llarg de les arestes. La melanoflogita és una forma metaestable de SiO₂ que s'estabilitza en aquesta estructura a causa de molècules de gas atrapades a les gàbies. L'Associació de Zeolita Internacional utilitza el símbol MEP per indicar la topologia de marc de melanoflogita.
Aplicacions
[modifica]L'estructura Weaire–Phelan va inspirar el disseny del Pequín Nacional Aquatics Centre per als Jocs olímpics de 2008 de Pequín, Xina.[9] El sistema de suport estructural resultant és inherentment fort i lleuger. Atès que totes les juntes de l'estructura són properes a angles tetraèdrics, el marc omple un volum gran d'espai amb una quantitat reduïda de material, similar a un enrajolat en dues dimensions.
Vegeu també
[modifica]Referències
[modifica]- ↑ Weaire, D.; Phelan, R. «A counter-example to Kelvin's conjecture on minimal surfaces». Phil. Mag. Lett., 69, 2, 1994, p. 107–110. DOI: 10.1080/09500839408241577.
- ↑ Lord Kelvin (Sir William Thomson) «On the Division of Space with Minimum Partitional Area». Philosophical Magazine, 24, 151, 1887, p. 503. DOI: 10.1080/14786448708628135.
- ↑ Gabbrielli, Ruggero. «Ruggero Gabbrielli - Google Scholar Citations». scholar.google.com.
- ↑ Gabbrielli, Ruggero Philosophical Magazine Letters, 89, 8, 01-08-2009, pàg. 483–491. DOI: 10.1080/09500830903022651. ISSN: 0950-0839.
- ↑ Gabbrielli, R.; Meagher, A.J.; Weaire, D.; Brakke, K.A. «An experimental realization of the Weaire-Phelan structure in monodisperse liquid foam». Phil. Mag. Lett., 92, 2012, p. 1–6. DOI: 10.1080/09500839.2011.645898.
- ↑ Ball, Philip «Scientists make the 'perfect' foam: Theoretical low-energy foam made for real». Nature, 2011. DOI: 10.1038/nature.2011.9504.
- ↑ A diagram can be found in Pauling, Linus. The Nature of the Chemical Bond. 3rd. Cornell University Press, 1960, p. 471., as shown on Ken Brakke's page Arxivat 2008-08-20 a Wayback Machine..
- ↑ Frank, F. C.. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles, 1958, p. 184–190.. Frank, F. C.. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures, 1959, p. 483–499.
- ↑ Fountain, Henry «A Problem of Bubbles Frames an Olympic Design». New York Times, 05-08-2008.
