Experiment d'esborrador quàntic
En mecànica quàntica, un experiment d'esborrador quàntic és un experiment d'interferòmetre que demostra diversos aspectes fonamentals de la mecànica quàntica, incloent l'entrellat quàntic i la complementarietat.[1][2] :328 L'experiment d'esborrador quàntic és una variació del clàssic experiment de doble escletxa de Thomas Young. Estableix que quan es prenen mesures per determinar per quina de les 2 escletxes ha passat un fotó, el fotó no pot interferir amb si mateix. Quan un corrent de fotons es marca d'aquesta manera, no es veuran les franges d'interferència característiques de l'experiment de Young. L'experiment també crea situacions en què un fotó que s'ha "marcat" per revelar per quina escletxa ha passat es pot "desmarcar". Un fotó que ha estat "sense marcar" interferirà amb si mateix una vegada més, restaurant els serrells característics de l'experiment de Young.[3]
Història
[modifica]L'experiment de l'esborrador quàntic es va proposar l'any 1982 a Marlan Scully i Kai Drühl a l'article "Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics", com a forma realitzable de provar les prediccions de la mecànica quàntica fins ara no provades. Com a inspiració, el document esmenta l'enfocament d'Eugene Wigner en el problema de la mesura, les converses amb Willis Lamb i els experiments mentals de John Archibald Wheeler. El document també assenyala que l'experiment es podria executar en mode d'elecció retardada, tal com es va conceptualitzar pels experiments de pensament de Wheeler, el que ara es coneix com a esborrador quàntic d'elecció retardada.[4]
L'experiment
[modifica]Concepte
[modifica]Aquest experiment implica un aparell amb dues seccions principals. Després de crear dos fotons entrellaçats, cadascun es dirigeix a la seva pròpia secció de l'aparell. Qualsevol cosa que es faci per conèixer el camí de la parella enredada del fotó que s'està examinant a la part de doble escletxa de l'aparell influirà en el segon fotó, i viceversa. L'avantatge de manipular els socis entrellaçats dels fotons a la part de doble escletxa de l'aparell experimental és que els experimentadors poden destruir o restaurar el patró d'interferència en aquest últim sense canviar res en aquesta part de l'aparell. Els experimentadors ho fan manipulant el fotó enredat, i ho poden fer abans o després que el seu soci hagi passat per les ranures i altres elements de l'aparell experimental entre l'emissor de fotons i la pantalla de detecció. En condicions en què la part de doble escletxa de l'experiment s'ha configurat per evitar l'aparició de fenòmens d'interferència (perquè hi ha informació definitiva de "quina ruta" present), l'esborrador quàntic es pot utilitzar per esborrar efectivament aquesta informació. En fer-ho, l'experimentador restaura la interferència sense alterar la part de doble escletxa de l'aparell experimental.[5]
Una variació d'aquest experiment, l'esborrador quàntic d'elecció retardada, permet que la decisió de mesurar o destruir la informació de "quina ruta" es retardi fins que la partícula parella entrellaçada (la que passa per les escletxes) hagi interferit amb ella mateixa o no.[6] En experiments d'elecció retardada, els efectes quàntics poden imitar una influència d'accions futures en esdeveniments passats.[7] Tanmateix, l'ordre temporal de les accions de mesura no és rellevant.[8]
Procediment
[modifica]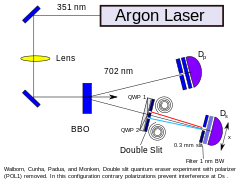
En primer lloc, es dispara un fotó a través d'un dispositiu òptic no lineal especialitzat: un cristall de borat de bari beta (BBO).[9] Aquest cristall converteix el fotó únic en dos fotons entrellaçats de menor freqüència, un procés conegut com a conversió paramètrica a la baixa espontània (SPDC). Aquests fotons entrellaçats segueixen camins separats. Un fotó va directament a un detector de resolució de polarització, mentre que el segon fotó passa per la màscara de doble escletxa a un segon detector de resolució de polarització. Tots dos detectors estan connectats a un circuit de coincidència, assegurant que només es compten els parells de fotons entrellaçats. Un motor pas a pas mou el segon detector per escanejar l'àrea objectiu, produint un mapa d'intensitat. Aquesta configuració produeix el patró d'interferència familiar.
A continuació, es col·loca un polaritzador circular davant de cada escletxa a la màscara de doble escletxa, produint una polarització circular en el sentit de les agulles del rellotge en la llum que passa per una escletxa i una polarització circular en sentit contrari a les agulles del rellotge a l'altra escletxa (vegeu la figura 1). (Quina escletxa correspon a quina polarització depèn de la polarització informada pel primer detector.) Aquesta polarització es mesura al segon detector, "marcant" així els fotons i destruint el patró d'interferència (vegeu lleis de Fresnel-Arago).
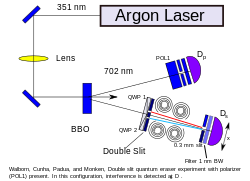
Finalment, s'introdueix un polaritzador lineal en el camí del primer fotó del parell entrellat, donant a aquest fotó una polarització diagonal (vegeu la figura 2). L'entrellat assegura una polarització diagonal complementària en la seva parella, que passa per la màscara de doble escletxa. Això altera l'efecte dels polaritzadors circulars: cadascun produirà una barreja de llum polaritzada en sentit horari i en sentit contrari a les agulles del rellotge. Així, el segon detector ja no pot determinar quin camí s'ha pres, i es restableixen les franges d'interferència.
També es pot tenir en compte una doble escletxa amb polaritzadors giratoris considerant que la llum és una ona clàssica.[10] Tanmateix, aquest experiment utilitza fotons entrellaçats, que no són compatibles amb la mecànica clàssica.
Altres aplicacions
[modifica]La tecnologia d'esborrat quàntic es pot utilitzar per augmentar la resolució dels microscopis avançats.[11]
Equívoc comú
[modifica]Un malentès comú sobre aquest experiment és que es pot utilitzar per comunicar informació instantàniament entre dos detectors. La simple causalitat, però, impedeix la imposició d'informació "donada" sobre els resultats observats. És important entendre el paper del detector de coincidències en aquesta configuració experimental. El polaritzador lineal del camí superior filtra efectivament la meitat dels fotons entrellaçats i, mitjançant el detector de coincidències, filtra els fotons corresponents del camí inferior. El detector de coincidències només pot funcionar comparant dades d'ambdós sensors, cosa que fa impossible utilitzar aquesta configuració per a la comunicació instantània.
Un malentès comú sobre aquest experiment és que es pot utilitzar per comunicar informació instantàniament entre dos detectors. La simple causalitat, però, impedeix la imposició d'informació "donada" sobre els resultats observats. És important entendre el paper del detector de coincidències en aquesta configuració experimental. El polaritzador lineal del camí superior filtra efectivament la meitat dels fotons entrellaçats i, mitjançant el detector de coincidències, filtra els fotons corresponents del camí inferior. El detector de coincidències només pot funcionar comparant dades d'ambdós sensors, cosa que fa impossible utilitzar aquesta configuració per a la comunicació instantània.
Tingueu en compte que a l'estat final d'aquesta configuració experimental, les mesures del camí inferior sempre mostren un patró tacat a les dades en brut. Veure un patró d'interferència només és possible filtrant les dades amb el detector de coincidències i mirant només fotons que eren 1/2 d'un parell entrellaçat.
Referències
[modifica]- ↑ Englert, Berthold-Georg Zeitschrift für Naturforschung, 54, 1, 1999, pàg. 11–32. Bibcode: 1999ZNatA..54...11E. DOI: 10.1515/zna-1999-0104 [Consulta: 10 abril 2019].
- ↑ Baggott, J. E.. The quantum story: a history in 40 moments. Impression: 3. Oxford: Oxford Univ. Press, 2013. ISBN 978-0-19-965597-7.
- ↑ Walborn, S. P.; Terra Cunha, M. O.; Pádua, S.; Monken, C. H. (en anglès) Physical Review A, 65, 3, 20-02-2002. arXiv: quant-ph/0106078. DOI: 10.1103/PhysRevA.65.033818. ISSN: 1050-2947.
- ↑ Scully, Marian O.; Drühl, Kai Physical Review A, 25, 4, 1982. DOI: 10.1103/PhysRevA.25.2208.
- ↑ Walborn, S. P.; Terra Cunha, M. O.; Pádua, S.; Monken, C. H. (en anglès) Physical Review A, 65, 3, 20-02-2002. arXiv: quant-ph/0106078. DOI: 10.1103/PhysRevA.65.033818. ISSN: 1050-2947.
- ↑ Yoon-Ho, Kim; Yu, R.; Kulik, S.P.; Shih, Y.H.; Scully, Marlan Physical Review Letters, 84, 1, 2000, pàg. 1–5. arXiv: quant-ph/9903047. Bibcode: 2000PhRvL..84....1K. DOI: 10.1103/PhysRevLett.84.1. PMID: 11015820.
- ↑ Fankhauser, Johannes Quanta, 8, 2019, pàg. 44–56. arXiv: 1707.07884. DOI: 10.12743/quanta.v8i1.88.
- ↑ Ma, Xiao-song; Kofler, Johannes; Zeilinger, Anton Rev. Mod. Phys., 88, 1, 2016, pàg. 015005. arXiv: 1407.2930. Bibcode: 2016RvMP...88a5005M. DOI: 10.1103/RevModPhys.88.015005.
- ↑ Walborn, S. P.; Terra Cunha, M. O.; Pádua, S.; Monken, C. H. (en anglès) Physical Review A, 65, 3, 20-02-2002. arXiv: quant-ph/0106078. DOI: 10.1103/PhysRevA.65.033818. ISSN: 1050-2947.
- ↑ Chiao, R Y; Kwia, P G; Steinberg, A M Quantum and Semiclassical Optics: Journal of the European Optical Society Part B, 7, 3, 6-1995, pàg. 259–278. arXiv: quant-ph/9501016. Bibcode: 1995QuSOp...7..259C. DOI: 10.1088/1355-5111/7/3/006.
- ↑ Aharonov, Yakir; Zubairy, M. Suhail Science, 307, 5711, 2005, pàg. 875–879. Bibcode: 2005Sci...307..875A. DOI: 10.1126/science.1107787. PMID: 15705840.
