Fatiga mecànica

La fatiga és, en la ciència dels materials, un tipus de trencament que es produeix en una peça d'una màquina o a un element d'una estructura a causa de tensions dinàmiques cícliques o fluctuants, és a dir, que el valor de la tensió no és continu, sinó que varia amb el temps, i pot ser en alguns moments nul. S'ha de tenir en compte en fer els càlculs per al disseny de màquines i estructures, ja que en general el trencament per fatiga suposa la fi de la vida de la màquina o estructura completa. En el cas d'una estructura, d'un edifici o d'un pont, per exemple, pot suposar el seu esfondrament. En el cas d'una màquina, a més d'una aturada no desitjada, pot suposar greus accidents.
La fatiga és la primera causa de trencament dels materials ceràmics, polímers i sobretot metàl·lics, dels quals un 90% dels trencaments són d'aquesta mena.[1] És molt habitual, per exemple, en avions, ponts i components de màquines de tota mena. La resistència a la fatiga, la vida a fatiga i el límit de fatiga (o de resistència a la fatiga) són propietats mecàniques que es poden conèixer a partir d'assajos.
Els psiquiatres i psicòlegs es van inspirar d'aquest comportament físic dels materials sotmesos a tensions potser petites però sempre de manera continuada per a donar nom a l'"estrès" (és a dir, fatiga, en anglès) que poden patir les persones o altres éssers vius.
Etapes
[modifica]El trencament per fatiga consta de tres etapes: inici, propagació i trencament. La propagació es divideix en dues etapes fonamentals, la primera etapa de propagació, lenta i subtil, i la segona, a continuació, inesperada, ràpida i brusca.[1]
- Inici: S'inicia una molt petita escletxa en un punt dels que tenen major concentració de tensions. Sol ser a l'exterior i en un colze de la peça, un cantó, una ranura, o una ratlladura, per exemple.
- Propagació: L'escletxa creix i es propaga a cada cicle de càrrega, per exemple, en una roda, a cada volta que fa, o en un pont, a cada cop que algú el travessa. La velocitat de propagació es pot conèixer i calcular. Aquesta etapa en realitat es pot dividir en dues:
- Primera etapa de propagació: una primera molt subtil, que només es pot observar microscòpicament, i molt lenta. En metalls policristal·lins l'escletxa és de només d'uns quants grans de llargària en aquesta etapa.
- Segona etapa de propagació: en aquesta etapa, que pot no existir, l'escletxa creix de manera molt ràpida i la direcció de propagació canvia, de ser paral·lela a perpendicular a la tensió aplicada. Es produeixen estries de fatiga de mida microscòpica, observables amb microscopis electrònics TEM o SEM. De vegades, a més d'estries (marques lineals paral·leles) es formen també marques anomenades de petxina, que són marques circulars que poden recordar les ranures de la closca d'una escopinya.
- Trencament: Quan l'escletxa assoleix un certa mida crítica, es produeix de manera sobtada i molt ràpida (es considera instantani) un gran trencament.
Diagnosi
[modifica]
Quan s'observa la part trencada amb un microscopi electrònic i hi veiem unes petites línies al voltant, no observables a vista, sabem que segurament s'ha tractat d'un trencament per fatiga. Tanmateix, de vegades pot ser també per fatiga però que les línies no siguin visibles tampoc amb un microscopi.[1]
Disseny
[modifica]L'anomenada vida a fatiga, el temps que durarà fins a trencar-se per fatiga, es pot allargar calculant una tensió aplicada adequada. També per mitjà d'altres factors, com el disseny del component (evitant discontinuïtats, entalles, etc.), tractaments superficials (polir les petites ratlladures que inevitablement es formen en fabricar la peça, per exemple) i (als acers) l'enduriment superficial (carburació, cimentació, nitruració).[1]
Tipus
[modifica]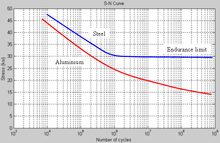
- Oligofatiga: O fatiga a baix nombre de cicles. La vida a fatiga és curta (menor de 104 cicles). Deformacions cícliques elàstiques i de vegades també plàstiques. Causada per a càrregues grans.[1]
- Fatiga a alt nombre de cicles: La vida a fatiga és superior (major de 10⁵ cicles), ja que les deformacions que es produeixen a cada cicle són sempre totalment elàstiques, de manera que necessita un nombre major de cicles fins que es trenqui.[1]
Cronologia de la fatiga mecànica
[modifica]- 1837. Wilhelm Albert, enginyer alemany, escrigué el primer treball sobre la fatiga mecànica. [2]
- 1839. Jean Victor Poncelet.[3][4]
- 1842. William John Macquorn Rankine.[5]
- 1843. Joseph Glynn va informar de la fatiga d’un eix pertanyent a un tènder de locomotora. Identificà la xaveta com a responsable.[6]
- 1848. L’organisme Railway Inspectorate informava dels primers tipus de falla de les llandes. Probablement atribuïble a la fatiga.[7]
- 1849. Eaton Hodgkinson fou recompensat amb una modesta quantitat de diners per haver informat al Parlament britànic de les seves recerques pràctiques sobre la variació continuada d’esforços sobre estructures de ferro. I haver proporcionat detalls sobre les càrregues màximes segures.[8]
- 1854. F. Braithwaite.[9]
- 1860. William Fairbairn [10] i AugustWöhler.[11] Proves sistemàtiques sobre la fatiga.
- 1870. August Wöhler presentà les conclusions dels seus assaigs sobre eixos de ferrocarrils. Destacà que el rang de variació de les tensions cícliques era més important que les tensions màximes. Introduí el concepte de límit de fatiga.[12]
- 1903. James Alfred Ewing. Determinà que l’origen de la fatiga eren les microfractures.[13]
- 1910. O.H.Basquin.[14]
- 1940. Sidney M. Cadwell va publicar el primer estudi seriós sobre la fatiga en peces de cautxú.[15]
- 1945. A.M. Miner va divulgar el mètode de Palmgren ( de 1924) com a eina pràctica de disseny.[16]
- 1952. W.Weibull.[17]
- 1954. Triple accident del model d’avió Haviland Comet que va provocar canvis de disseny.[18]
- 1954. L.F. Coffin i S.S.Manson explicaren el creixement d’una esquerda a partir de la deformació plàstica dels extrems de l’esquerda.[19]
- 1961. P.C.Paris. Proposà mètodes de predicció del creixement d’esquerdes individuals en front de l’escepticisme inicial i del corrent popular que seguia el mètode de Miner.[20]
- 1968. Tatsuo Endo i M.Matsuishi proposaren l’algorisme de recompte de la pluja i permeteren una aplicació fiable de la regla de Miner per a càrregues aleatòries.[21]
- 1970. Smith, Watson i Topper presentaren un model de correcció basat en que el dany en un cicle es determinava pel producte de la tensió màxima i el valor (amplitud) de la deformació.[22]
- 1970. W.Elber.[23]
- 1973. Treballs de M.W.Brown i K.J.Miller.[24]
- 2013.[25]
Referències
[modifica]- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 W.D. Callister Jr, Ciencia e ingeniería de los materiales, Volum I, Editorial Reverté, Barcelona, 1995, (castellà) (anglès) ISBN 84-291-7253-X
- ↑ Cotterell, B. Fracture and Life. Imperial College Press, 2010, p. 174. ISBN 978-1-84816-283-9.
- ↑ Ohnami, M. Fracture and Society. Ohmsha, 1992, p. 85. ISBN 978-90-5199-092-8.
- ↑ Poncelet, J.V.; Schiwel, J. Traité de mécanique appliquée aux machines (en francès). Jean Schiwel, 1844, p. 191 (Traité de mécanique appliquée aux machines).
- ↑ Ohnami, M. Fracture and Society. Ohmsha, 1992, p. 86. ISBN 978-90-5199-092-8.
- ↑ Cotterell, B. Fracture And Life. World Scientific Publishing Company, 2010, p. 176. ISBN 978-1-908978-67-7.
- ↑ OECD. Safety and Regulatory Reform of Railways. OECD Publishing, 2010, p. 30 (Transport Research Centre). ISBN 978-92-821-0283-1.
- ↑ Harter, H.L.. A Survey of the Literature on the Size Effect on Material Strength. Air Force Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, Air Force Systems Command, 1977, p. 409 (Technical report (Air Force Flight Dynamics Laboratory (U.S.)))).
- ↑ Vassilopoulos, A.P.. Fatigue Life Prediction of Composites and Composite Structures. Elsevier Science, 2019, p. 1 (Woodhead Publishing Series in Composites Science and Engineering). ISBN 978-0-08-102576-5.
- ↑ Box, T. A Practical Treatise on the Strength of Material: Including Their Elasticity and Resistance to Impact. E. & F.N. Spon, 1883, p. 477.
- ↑ Straub, T. Experimental Investigation of Crack Initiation in Face-Centered Cubic Materials in the High and Very High Cycle Fatigue Regime. KIT Scientific Publishing, 2016, p. 4 (Schriftenreihe des Instituts fuer Angewandte Materialien, Karlsruher Institut fuer Technologie). ISBN 978-3-7315-0471-9.
- ↑ Pook, L.P.. Metal Fatigue: What It Is, Why It Matters. Springer Netherlands, 2007, p. 85 (Solid Mechanics and Its Applications). ISBN 978-1-4020-5597-3.
- ↑ Newman, J.C.; Elber, W. Mechanics of Fatigue Crack Closure. ASTM, 1988, p. 6 (ASTM STP 982). ISBN 978-0-8031-0996-4.
- ↑ Giudice, F.; Rosa, G.L.; Risitano, A. Product Design for the Environment: A Life Cycle Approach. CRC Press, 2006, p. 291. ISBN 978-1-4200-0104-4.
- ↑ Bhowmick, A.K.. Current Topics in Elastomers Research. CRC Press, 2008, p. 683. ISBN 978-1-4200-0718-3.
- ↑ Straub, D. Generic Approaches to Risk Based Inspection Planning for Steel Structures. vdf Hochschulverlag AG an der ETH Zürich, 2004, p. 39 (Bericht (Institut für Baustatik und Konstruktion ETH Zürich)). ISBN 978-3-7281-2969-7.
- ↑ Lauraitis, K.N.. Fatigue of Fibrous Composite Materials. ASTM International, 1981, p. 133.
- ↑ Jones, D.R.H.. Failure Analysis Case Studies II. Elsevier Science, 2013, p. 185. ISBN 978-0-08-054555-4.
- ↑ Gomatam, R.; Mittal, K.L.. Electrically Conductive Adhesives. Taylor & Francis, 2008, p. 262. ISBN 978-90-04-16592-2.
- ↑ Engle, R.M.. Cracks, a Fortran IV Digital Computer Program for Crack Propagation Analysis. Air Force Flight Dynamics Laboratory, Air Force Systems Command, United States Air Force, 1970, p. 2 (Technical report (Air Force Flight Dynamics Laboratory (U.S.)))).
- ↑ Murakami, Y. The Rainflow Method in Fatigue: The Tatsuo Endo Memorial Volume. Elsevier Science, 2013, p. 4. ISBN 978-1-4831-6142-6.
- ↑ McDowell, D.L.; Ellis, R. Advances in Multiaxial Fatigue. ASTM, 1993, p. 144 (ASTM STP 1191). ISBN 978-0-8031-1862-1.
- ↑ Orringer, O.; Orkisz, J.; Świderski, Z. Residual stress in rails :: effects on rail integrity and railroad economics. Springer Netherlands, 1992, p. 98 (Engineering application of fracture mechanics). ISBN 978-0-7923-1635-0.
- ↑ Ngo, A.D.. Design, Manufacturing and Applications of Composites: Proceedings of the Eighth Joint Canada-Japan Workshop on Composites : École de Technologie Supérieure, Montréal, Québec, Canada ; Industrial Materials Institute, Boucherville, Québec, Canada : July 26-29, 2010 (en francès). DEStech Publications, 2010, p. 163. ISBN 978-1-60595-028-0.
- ↑ Server, N.T.R.. Effectiveness of Shot Peening in Suppressing Fatigue Cracking at Non-Metallic Inclusions in Udimet. BiblioLife, 2013. ISBN 978-1-289-25448-3.
Enllaços externs
[modifica]- Caracteritzacio de la resposta a la fatiga Azterlan, centro metalúrgico de investigación. 2004 (castellà)
- Granallat de pretensionat III: Comportament sota fatiga a alt nombre de cicles Arxivat 2007-09-28 a Wayback Machine. Jornadas SAM 2000: IV Coloquio Latinoamericano de Fractura y Fatiga, Argentina, agost de 2000.(castellà)
