Mecànica
| Aquest article tracta sobre la mecànica com una part de la física. Si cerqueu mecànica aplicada a la tecnologia, vegeu «Enginyeria mecànica». |

La mecànica (del grec Μηχανική mekanicos) és la part de la física que estudia el moviment dels cossos físics i les causes d'aquests moviments, tals com les forces o les energies. La mecànica pot ser dividida en la mecànica clàssica, la mecànica relativista, la mecànica quàntica i la mecànica quàntica relativista. Aquesta divisió depèn de la dimensió i la velocitat dels objectes físics que s'estudien. Aquesta disciplina té els seus inicis a l'antiga Grècia però és a l'edat moderna, amb científics com Galileo, Kepler i especialment Newton, quan s'inicia el que avui coneixem com a mecànica clàssica.
La mecànica és una ciència que pertany a la física, ja que estudia fenòmens físics. Per això té una estreta relació amb el rigor de les matemàtiques i el seu raonament deductiu, així com amb l'enginyeria, amb un caràcter fortament empíric.
Història
[modifica]Alguns filòsofs grecs de l'antiguitat, particularment Aristòtil,[1] ja van introduir la idea de l'existència de principis abstractes que governaven la natura. Un desenvolupament posterior va ser fet per Hiparc de Nicea.[2]
Per una altra banda, alguns conceptes relacionats amb les lleis de Newton del moviment van ser enunciats per alguns físics musulmans durant l'edat mitjana. Una versió inicial de la llei de la inèrcia (primera llei de Newton) i el concepte de quantitat de moviment (una part de la segona llei de Newton) van ser descrits per Alhazen (965-1040)[3][4] i Avicenna (980-1037).[5][6] La proporcionalitat entre força i acceleració, un principi important en mecànica clàssica, va ser postulat per primera vegada per Abu-l-Barakat (1077-1165),[7] i teories sobre la gravetat van ser desenvolupades per Banu Mussa,[8] Alhazen,[9] i al-Khaziní.[10] És sabut que el tractat sobre l'acceleració de Galileo Galilei i el seu concepte de la inèrcia (impetus)[11] va sorgir a partir de l'anàlisi anterior del moviment que a l'edat mitjana havien fet Avicenna,[5] Avempace,[12] i Jean Buridan (1300-1358).
A Europa la primera explicació de les causes del moviment dels planetes va ser l'obra Astronomia nova que Johannes Kepler va publicar el 1609. Aquest trencament amb el pensament antic va coincidir amb la proposta de Galileu d'unes lleis matemàtiques abstractes sobre el moviment dels planetes. Els seus experiments sobre la gravetat, publicats el 1590 a De Motu (En Moviment) i al 1600 Le Meccaniche (Mecànica), va permetre a Galileu la formulació de la seva teoria sobre l'acceleració, reflectida a la seva obra Discorsi e dimostrazioni matematiche, intorno à due nuove scienze (Discurs i demostració matemàtica, entorn de dues noves ciències) publicat el 1638, constitueix una pedra angular de la mecànica clàssica[13] i marca la fi de la física aristotèlica.
Newton postula la mecànica clàssica
[modifica]
Isaac Newton va proposar per primer cop juntes les tres lleis del moviment: la llei de la inèrcia, la llei de l'acceleració, i la llei de llei d'acció i reacció, que serien els fonaments de la mecànica clàssica. Tant la segona com tercera lleis de Newton van ser objecte d'un tractament científic i matemàtic adequat a la seva obra Philosophiae Naturalis Principia Mathematica el 1687. També va ser el primer a oferir la primera formulació científica i matemàtica de la gravetat a la seva llei de la gravitació universal. Després de Newton la mecànica clàssica va esdevenir el camp principal d'estudi en matemàtiques i en física.
Leonhard Euler el 1750 va introduir una generalització de les lleis de Newton anomenades lleis del moviment d'Euler, vàlides per a cossos deformables, donant peu a la formulació de la mecànica dels medis continus.
Entre 1772 i 1788, Joseph-Louis Lagrange va reformular la mecànica vectorial d'Isaac Newton per facilitar-ne els càlculs. Lagrange descriu en el seu tractat La mecànica analítica una extensió de la llei del treball virtual, i fa d'ell un principi fonamental de la mecànica, amb l'ajuda del càlcul de variacions presenta una nova formulació coneguda com a mecànica lagrangiana.
El 1833 William Rowan Hamilton defineix, a partir de la formulació lagrangiana, una altra reformulació de la mecànica clàssica coneguda com a mecànica hamiltoniana. Un dels principals avantatges d'aquesta mecànica és el fet que fa servir una metodologia que condueix a un coneixement més profund de la mecànica. Apareix el concepte de hamiltonià que permetrà, més endavant, la formulació de la mecànica quàntica.
A finals del segle xix es van descobrir algunes dificultats que només van poder ser resoltes amb una física més moderna. Algunes d'aquestes dificultats eren relacionades amb la compatibilitat amb la teoria electromagnètica i el famós experiment de Michelson-Morley, la resolució del qual va portar a l'aparició de la teoria de la relativitat especial, que sovint és inclosa dins la mecànica clàssica.
Des de finals del segle xx la mecànica clàssica ja no és considerada com una teoria independent. L'èmfasi s'ha posat en els esforços per comprendre les forces fonamentals de la natura com en el cas del model estàndard de física de partícules i les seves extensions més modernes vers una teoria del tot.[14] Per tant, en l'actualitat la mecànica clàssica és una teoria per a l'estudi del moviment en un entorn fóra de l'àmbit de la mecànica quàntica, amb partícules de baixa energia i camps gravitacionals febles.
L'arribada de la mecànica quàntica
[modifica]Els fonaments de la mecànica quàntica es van establir durant la primera meitat del segle xx per Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, David Hilbert, entre d'altres. Els desenvolupaments fets a mitjans dels anys vint amb la mecànica quàntica van portar a la formulació de la física atòmica. El 1925, Bohr i Heisenberg van publicar els resultats que tancaven l'antiga teoria quàntica (Old Quantum Theory). El 1926 apareix el concepte de fotó, que permet la dualitat entre matèria i energia de la llum. L'acceptació definitiva de la mecànica quàntica va esdevenir durant la Fifth Solvay Conference el 1927.
Mecànica clàssica
[modifica]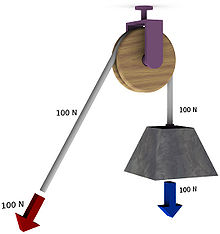
La mecànica clàssica descriu amb molta precisió la majoria dels fenòmens de l'experiència quotidiana. El seu rang de validesa va des del moviment de les cèl·lules dins el cos humà fins al moviment dels planetes al sistema solar, passant per tots els moviments dels objectes que ens trobem a la nostra vida diària. Quan les velocitats dels objectes s'aproximen a la velocitat de la llum, la mecànica clàssica perd la seva validesa i és reemplaçada per la mecànica relativista. Quan anem a escales atòmiques també perd la seva validesa i és reemplaçada per la mecànica quàntica.
Mecànica newtoniana
[modifica]La mecànica newtoniana, també anomenada mecànica vectorial, és la formulació més coneguda i la més senzilla de la mecànica clàssica. Basada en les Lleis de Newton, en honor de les contribucions fonamentals a aquesta teoria per Isaac Newton, i que requereix l'ús d'uns sistemes de referència inercial. Permet l'estudi del moviment de partícules i sòlids en un espai euclidi tridimensional.
- Estàtica, que estudia els cossos en repòs a través del seu equilibri de forces i moments.
- Cinemàtica, que estudia el moviment dels cossos des d'un punt de vista purament geomètric, sense tenir-ne en compte les forces que actuen sobre ells.
- Dinàmica, que estudia el moviment dels cossos tenint en compte les forces que actuen sobre ells.
Mecànica analítica
[modifica]És usada per descriure de forma més matemàtica la mecànica clàssica, formulada inicialment per Isaac Newton. De fet és un formalisme de la mecànica clàssica que es basa en una anàlisi variacional de l'equilibri energètic entre l'energia cinètica i l'energia potencial.
- Mecànica lagrangiana. La formulació lagrangiana identifica el camí actual seguit pel moviment com una selecció del camí sobre el qual la integral temporal de l'energia cinètica és menor, assumint l'energia total constant i sense imposar condicions en el temps de trànsit.
- Mecànica hamiltoniana. La formulació hamiltoniana és més general; permet que l'energia depengui del temps. Identifica el camí seguit que sigui el que tingui menys acció (la integral sobre el camí de la diferència entre les energies cinètica i potencial) amb els temps de sortida i arribada constants.[15]
Mecànica aplicada
[modifica]- Mecànica celeste. És una branca de l'astronomia i la mecànica clàssica que té per objecte l'estudi dels moviments dels cossos en virtut dels efectes gravitatoris que exerceixen sobre ells altres cossos celestes.
- Mecànica dels medis continus. Tracta els cossos materials deformables extensos i que no poden ser tractats com sistemes amb un nombre finit de graus de llibertat. Aquesta disciplina compren:
- Mecànica dels sòlids, que considera els fenòmens de l'elasticitat, la resistència de materials, la plasticitat, la degradació, la viscoelasticidad, etc. També engloba altres branques de la mecànica aplicada com la mecànica de la fractura o la mecànica dels sòls.
- Mecànica dels fluids, que comprèn un conjunt de teories parcials com la hidràulica, la hidroestàtica i la hidrodinàmica. Es distingeix l'estudi de fluid compressible i fluid incompressible. Si es té en compte la seva equació constitutiva, es té un fluid perfecte, fluid newtonià o fluid no-newtonià.
- Acústica i la mecànica ondulatòria clàssica
- Biomecànica és l'aplicació dels principis mecànics a sistemes biològics. Una de les millors definicions de la biomecànica prové de Herbert Hatze el 1974: Biomechanics is the study of the structure and function of biological systems by means of the methods of mechanics. La biomecànica és propera a l'enginyeria, ja que usa sovint l'enginyeria per analitzar els sistemes biològics.
Mecànica estadística
[modifica]La mecànica estadística tracta els sistemes amb moltes partícules amb un nombre elevat de graus de llibertat, de manera que no es poden escriure totes les equacions de moviment involucrades. Per tant, la mecànica estadística tracta de resoldre aspectes parcials del sistema per mètodes estadístics que donen informació sobre el comportament global del sistema sense saber que passa en cada una de les partícules. Els resultats obtinguts coincideixen amb els de la termodinàmica. Empra formulacions tant de la mecànica hamiltoniana com de la teoria de la probabilitat.
Mecànica relativista
[modifica]La mecànica relativista o teoria de la relativitat comprèn:
- La teoria de la relativitat especial, que descriu adequadament el comportament clàssic dels cossos que es mouen a grans velocitats en un espaitemps pla (no-corbat).
- La teoria general de la relativitat, que generalitza l'anterior descrivint el moviment en espais-temps corbs, a més engloba una teoria relativista de la gravitació que generalitza la llei de la gravitació universal de Newton.
La mecànica relativista té algunes diferències importants respecte a la mecànica newtoniana. Una de les propietats interessants de la dinàmica relativista és que la força i l'acceleració no són en general vectors paral·lels en una trajectòria corba. De fet, la relació entre l'acceleració tangencial i la força tangencial és diferent que la que existeix entre l'acceleració i forces normals. Tampoc és constant el quocient entre els mòduls de la força i l'acceleració (en la mecànica newtoniana és la massa o la inèrcia), que apareix l'invers del factor de Lorentz, que decreix amb la velocitat arribant a ser nul a velocitats properes a la velocitat de la llum. Tot i això, malgrat les diferències, la mecànica relativista és molt més similar a la mecànica clàssica, des d'un punt de vista formal, que a la mecànica quàntica. Per exemple, és una teoria estrictament determinista igual que la mecànica newtoniana.
Mecànica quàntica
[modifica]| Mecànica quàntica |
|---|
 |
|
Principi d'incertesa Història de la mecànica quàntica Cronologia de la mecànica quàntica |
|
Conceptes fonamentals |
|
Científics Bell · Bohm · Bohr · Born · Bose · de Broglie · Dirac · Ehrenfest · Everett · Feynman · Heisenberg · Jordan · Kramers · von Neumann · Pauli · Planck · Schrödinger · Sommerfeld · Wien · Wigner · Salam · Riazuddin |
La mecànica quàntica és coneguda també com a mecànica ondulatòria i com a física quàntica, és la branca de la física que estudia el comportament de la llum i de la matèria a escala atòmica i subatòmica. Els seus principis bàsics s'apliquen a molts dels camps de la física i la química actuals com, per exemple, la física de partícules, la física nuclear, la física de la matèria condensada, la física atòmica i molecular, la computació quàntica, l'òptica quàntica, la química quàntica i la química computacional.
Mecànica quàntica relativista
[modifica]La mecànica quàntica relativista tracta d'unir la mecànica relativista i la mecànica quàntica. El seu desenvolupament porta a la conclusió que en un sistema quàntic relativista el nombre de partícules no es conserva. Per tant, de fet no es pot parlar d'una mecànica de partícules, sinó d'una teoria quàntica de camps. Aquesta teoria no aconsegueix incorporar els principis de la relativitat general. Amb ella no es consideren estats de les partícules, sinó de l'espaitemps.
Referències
[modifica]- ↑ "A history of mechanics". René Dugas (1988). p.19. ISBN 0486656322
- ↑ "A Tiny Taste of the History of Mechanics". The University of Texas at Austin.
- ↑ Abdus Salam (1984), "Islam and Science". C. H. Lai (1987), Ideals and Realities: Selected Essays of Abdus Salam, 2a ed., World Scientific, Singapur, pàg. 179-213.
- ↑ Seyyed Hossein Nasr, "The achievements of Ibn Sina in the field of science and his contributions to its philosophy", Islam & Science, Desembre 2003.
- ↑ 5,0 5,1 Fernando Espinoza (2005). "An analysis of the historical development of ideas about motion and its implications for teaching", Physics Education 40 (2), pàg. 141.
- ↑ Seyyed Hossein Nasr, "Islamic Conception Of Intellectual Life", Philip P. Wiener (ed.), Dictionary of the History of Ideas, Vol. 2, pàg. 65, Charles Scribner's Sons, Nova York, 1973-1974.
- ↑ Shlomo Pines. «Abu'l-Barakāt al-Baghdādī, Hibat Allah». A: Dictionary of Scientific Biography. 1. Nova York: Charles Scribner's Sons, 1970, p. 26-28. ISBN 0684101149.
(Abel B. Franco (October 2003). "Avempace, Projectile Motion, and Impetus Theory", Journal of the History of Ideas 64 (4), pàg. 521-546 [528] - ↑ Robert Briffault (1938). The Making of Humanity, pàg. 191.
- ↑ Nader El-Bizri (2006), "Ibn al-Haytham or Alhazen", Josef W. Meri (2006), Medieval Islamic Civilization: An Encyclopaedia, Vol. II, p. 343-345, Routledge, New York, London.
- ↑ Mariam Rozhanskaya i I. S. Levinova (1996), "Statics", Roshdi Rashed, ed., Encyclopaedia of the History of Arabic Science, Vol. 2, pàg. 622. Londres i Nova York: Routledge.
- ↑ Galileo Galilei, Two New Sciences, trad. Stillman Drake, (Madison: Univ. of Wisconsin Pr., 1974), pàg. 217, 225, 296-7.
- ↑ Ernest A. Moody (1951). "Galileo and Avempace: The Dynamics of the Leaning Tower Experiment (I)", Journal of the History of Ideas 12 (2), pàg. 163-193.
- ↑ Galileo Galilei, Dialogues Concerning Two New Sciences by Galileo Galilei. Translated from the Italian and Latin into English by Henry Crew and Alfonso de Salvio. With an Introduction by Antonio Favaro (Nova York: Macmillan, 1914). Chapter: The Motion of Projectiles
- ↑ A la pàgina 2-10 de l'obra Feynman Lectures on Physics es diu "For already in classical mechanics there was indeterminability from a practical point of view." (Perquè a la mecànica clàssica existia indeterminabilitat des d'un punt de vista pràctic.)
- ↑ Cornelius Lanczos. The variational principles of mechanics (en anglès). 4a ed.. Nova York: Dover Publications Inc., 1970, p. Introduction, pp. xxi–xxix. ISBN 0-486-65067-7.

