Fitxer:Spring resonance.gif
El contingut de la pàgina no s'admet en altres llengües.
Aparença
De la Viquipèdia, l'enciclopèdia lliure
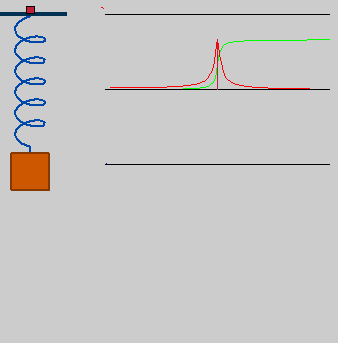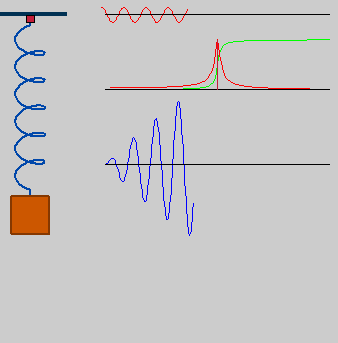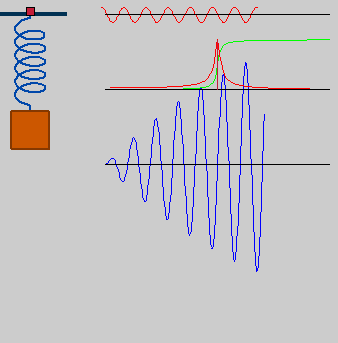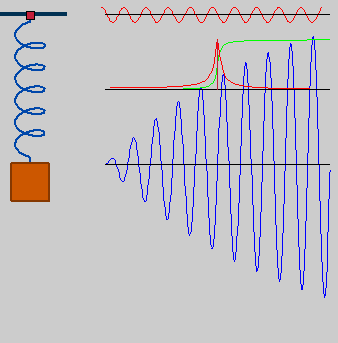
Spring_resonance.gif (338 × 343 píxels, mida del fitxer: 308 Ko, tipus MIME: image/gif, en bucle, 100 fotogrames, 5,0 s)
| Aquest fitxer i la informació mostrada a continuació provenen del dipòsit multimèdia lliure Wikimedia Commons. |
Resum
| DescripcióSpring resonance.gif |
Deutsch: getriebener Oszillator in Resonanz, omega_drive=omega0*1 |
| Data | |
| Font | Treball propi |
| Autor | Jkrieger |
base upon work by Oleg Alexandrov: [Simple harmonic oscillator.gif]
Aquesta GIF imatge rasteritzada ha estat creada amb MATLAB.
Source code
function main()
% colors
red = [0.867 0.06 0.14];
blue = [0 129 205]/256;
green = [0 200 70]/256;
black = [0 0 0];
white = [1 1 1]*0.99;
cardinal = [196 30 58]/256;
cerulean = [0 123 167]/256;
denim = [21 96 189]/256;
cobalt = [0 71 171]/256;
pblue = [0 49 83]/256;
teracotta= [226 114 91]/256;
tene = [205 87 0]/256;
wall_color = pblue;
spring_color = cobalt;
mass_color = tene;
exc_color=cardinal;
a=0.65; bmass_color = a*mass_color+(1-a)*black;
% linewidth and fontsize
lw=2;
fs=20;
ww = 0.5; % wall width
ms = 0.25; % the size of the mass
sw=0.1; % spring width
curls = 5;
exc_size=0.05;
plot_width=1.5; % width of plots
K_osz = 0.05; % excitation amplitude
omega =1; % excitation frequency
omega0=1; % eigen frequency
gamma=0.02; % damping factor
filename='spring_resonance.gif';
frames=100;
options = odeset('RelTol',1e-4,'AbsTol',1e-4);
[T,YODE] = ode45(@(t,y) dampedoszi(t,y,K_osz, omega, omega0, gamma),[0 20*pi],[0 0],options);
figure(2)
plot(T,YODE(:,1));
A = 0.2; % the amplitude of spring oscillations
B = -1; % the y coordinate of the base state (the origin is higher, at the wall)
% Each of the small lines has length l
l = 0.05;
N = length(T); % times per oscillation
No = 1; % number of oscillations
for f = 1:frames
i=floor(length(T)/frames*f);
% set up the plotting window
figure(1); clf; hold on; axis equal; axis off;
t = T(i); % current time
POSW=K_osz*sin(omega*t); % position of exciter with cos-excitation is a sine!
H= B+YODE(i); % position of the mass
%H=K/sqrt((1-omega).^2+(2*gamma*omega).^2)*cos(
% plot the spring from Start to End
Start = [0, POSW]; End = [0, POSW+H];
[X, Y]=do_plot_spring(Start, End, curls, sw);
plot(X, Y, 'linewidth', lw, 'color', spring_color);
% Here we cheat. We modify the point B so that the mass is attached exactly at the end of the
% spring. This should not be necessary. I am too lazy to to the exact calculation.
K = length(X); End(1) = X(K); End(2) = Y(K);
% plot the wall from which the spring is hanging
plot_wall(-ww/2, ww/2, l, lw, wall_color);
% plot the mass at the end of the spring
X=[-ms/2 ms/2 ms/2 -ms/2 -ms/2 ms/2]+End(1); Y=[0 0 -ms -ms 0 0]+End(2);
H=fill(X, Y, mass_color, 'EdgeColor', bmass_color, 'linewidth', lw);
% plot exciter
rectangle('Position',[0-exc_size/2,POSW-exc_size/2,exc_size,exc_size], 'FaceColor',exc_color)
% the bounding box
Sx = -0.4*ww; Sy = B-max(abs(YODE(:,1)))-ms-0.05;
Lx = ww+l+plot_width; Ly=l+K_osz;
axis([Sx, Lx, Sy, Ly]);
% plot amplitude time course
plot(ww+T(1:i)./max(T).*plot_width, B+YODE(1:i,1), 'b-');
line([ww ww+plot_width], [B B], 'Color', black);
plot(ww+(T(1:i)-1)./(max(T)+1).*plot_width, K_osz*cos(omega*T(1:i)), 'r-');
line([ww ww+plot_width], [0 0], 'Color', black);
% plot resonance curve
omeg=0.05:0.01:2;
phase=atan2(-2.*gamma.*omeg, (omega0.^2-omeg.^2));
amplitude=K./sqrt((omega0^2-omeg.^2).^2+(2*gamma*omeg).^2);
plot(ww+omeg./max(omeg).*plot_width, B/2+B/3*phase/abs(max(phase)-min(phase)), 'g-')
plot(ww+omeg./max(omeg).*plot_width, B/2-B/3*amplitude/abs(max(amplitude)-min(amplitude)), 'r-')
line([ww ww+plot_width], [B/2 B/2], 'Color', black);
rx=ww+omega/max(omeg).*plot_width;
line([rx rx], [B/2 B/2-B/3], 'Color', cardinal)
frame=getframe;
[im,map1] = rgb2ind(frame.cdata,32,'nodither');
if f==1
map=map1;
imwrite(im, map, filename, 'gif', 'WriteMode', 'overwrite', 'DelayTime', 0.05, 'LoopCount', Inf);
else
im= rgb2ind(frame.cdata,map);
imwrite(im, map, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.05);
end
disp(sprintf('Spring_frame%d', 1000+f)); %show the frame number we are at
pause(0.1);
end
function dy = dampedoszi(t,y, K, omega, omega0, gamma);
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = K*cos(omega*t)-2*gamma*y(2)-omega0^2*y(1);
function dy = damper(t,y, K, omega, omega0, gamma);
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = K*cos(omega*t);
function [X, Y]=do_plot_spring(A, B, curls, sw);
% plot a 3D spring, then project it onto 2D. theta controls the angle of projection.
% The string starts at A and ends at B
% will rotate by theta when projecting from 1D to 2D
theta=pi/6;
Npoints = 500;
% spring length
D = sqrt((A(1)-B(1))^2+(A(2)-B(2))^2);
X=linspace(0, 1, Npoints);
XX = linspace(-pi/2, 2*pi*curls+pi/2, Npoints);
Y=-sw*cos(XX);
Z=sw*sin(XX);
% b gives the length of the small straight segments at the ends
% of the spring (to which the wall and the mass are attached)
b= 0.05;
% stretch the spring in X to make it of length D - 2*b
N = length(X);
X = (D-2*b)*(X-X(1))/(X(N)-X(1));
% shift by b to the right and add the two small segments of length b
X=[0, X+b X(N)+2*b]; Y=[Y(1) Y Y(N)]; Z=[Z(1) Z Z(N)];
% project the 3D spring to 2D
M=[cos(theta) sin(theta); -sin(theta) cos(theta)];
N=length(X);
for i=1:N;
V=M*[X(i), Z(i)]';
X(i)=V(1); Z(i)=V(2);
end
% shift the spring to start from 0
X = X-X(1);
% now that we have the horisontal spring (X, Y) of length D,
% rotate and translate it to go from A to B
Theta = atan2(B(2)-A(2), B(1)-A(1));
M=[cos(Theta) -sin(Theta); sin(Theta) cos(Theta)];
N=length(X);
for i=1:N;
V=M*[X(i), Y(i)]'+A';
X(i)=V(1); Y(i)=V(2);
end
function plot_wall(S, E, l, lw, wall_color)
% Plot a wall from S to E.
no=20; spacing=(E-S)/(no-1);
plot([S, E], [0, 0], 'linewidth', 1.8*lw, 'color', wall_color);
Llicència
Jo, el titular dels drets d'autor d'aquest treball, el public sota la següent llicència:
Aquest fitxer està subjecte a la llicència de Creative Commons Reconeixement i Compartir Igual 3.0 No adaptada.
- Sou lliure de:
- compartir – copiar, distribuir i comunicar públicament l'obra
- adaptar – fer-ne obres derivades
- Amb les condicions següents:
- reconeixement – Heu de donar la informació adequada sobre l'autor, proporcionar un enllaç a la llicència i indicar si s'han realitzat canvis. Podeu fer-ho amb qualsevol mitjà raonable, però de cap manera no suggereixi que l'autor us dóna suport o aprova l'ús que en feu.
- compartir igual – Si modifiqueu, transformeu, o generareu amb el material, haureu de distribuir les vostres contribucions sota una llicència similar o una de compatible com l'original
Llegendes
Afegeix una explicació d'una línia del que representa aquest fitxer
Elements representats en aquest fitxer
representa l'entitat
Algun valor sense element de Wikidata
29 gen 2012
image/gif
Historial del fitxer
Cliqueu una data/hora per veure el fitxer tal com era aleshores.
| Data/hora | Miniatura | Dimensions | Usuari/a | Comentari | |
|---|---|---|---|---|---|
| actual | 17:19, 29 gen 2012 |  | 338 × 343 (308 Ko) | Jkrieger |
Ús del fitxer
La pàgina següent utilitza aquest fitxer:
Ús global del fitxer
Utilització d'aquest fitxer en altres wikis:
- Utilització a de.wikipedia.org
- Utilització a pt.wikipedia.org
- Utilització a ta.wikipedia.org