Ressonància

Ressonància és el fenomen pel qual un cos elàstic entra en vibració per contacte amb un altre cos vibrant dintre uns límits d’adequació freqüencial. En assolir-se aquesta harmonia, el primer cos augmenta, o pot augmentar, l'amplitud de les vibracions i es comporta com un ressonador.

La ressonància s'investigà inicialment en sistemes acústics com els instruments musicals i la veu humana. Un exemple de ressonància acústica és la vibració induïda en una corda de violí o de piano d’un to determinat quan es canta o toca a prop una nota musical del mateix to. El concepte de ressonància s’ha ampliat per analogia a determinats fenòmens mecànics, elèctrics, òptics, quàntics, etc.

Història

El botafumeiro de la catedral de Santiago de Compostel·la és un exemple d'un cos oscil·lant en ressonància. A cada oscil·lació la força que s'exerceix sobre ell n'augmenta l'amplitud, però no la freqüència.

A mitjan segle xvii, Galileo Galilei assenyalà que un home que llançava de la manera correcta d'un pèndol pesat podia conduir-lo a un moviment tan gran que podia aixecar fàcilment sis homes a l'aire. No obstant això, no pogué oferir cap tractament matemàtic i arribà a conclusions molt incorrectes sobre el que passa quan una força periòdica condueix un sistema oscil·latori natural. En particular, conclogué que el moviment resultant mai no es podria fer desviar-se de la freqüència natural inherent del sistema oscil·lant. Isaac Newton mai no tractà directament la qüestió del moviment impulsat d’un sistema mecànic harmònic no astronòmic. La primera comprensió moderna de la qüestió –i la correcció de l'error de Galileu– esperava el desenvolupament del càlcul al segle xviii, quan Leonhard Euler resolgué el problema mitjançant una equació diferencial. Conclogué que, en la condició de fora de ressonància, el moviment d'un sistema oscil·latori impulsat sense fricció o amortiment exhibiria dos components a freqüències diferents: la freqüència forçada i la freqüència natural del sistema impulsat. També considerà el cas de coincidència ressonant de les dues freqüències, concloent que l'amplitud de l'oscil·lació augmentaria linealment en el temps i potencialment sense límit.^[1]

Tanmateix Euler només considerà el problema com una curiositat matemàtica que no tenia gens d’importància pràctica. Els resultats d'Euler foren ignorats durant més d'un segle, fins que els redescobrí Thomas Young. Curiosament, però, Young només considerà el problema en relació amb l'anàlisi de les marees, de manera que el seu treball també fou ignorat posteriorment i no tingué cap impacte en la mecànica en general, ni en física ni en enginyeria. De fet, fins a finals del segle xix, els científics eren reticents a utilitzar el terme ‘ressonància’ en relació amb qualsevol cosa excepte els fenòmens acústics, d’on s'originà. L’ús de la paraula en altres camps –especialment en mecànica i en l’anàlisi de vibracions a les màquines– sempre inclogué alguna exempció de responsabilitat que l'enllaç era “només per analogia”, malgrat l'equivalència formal de les equacions dinàmiques fonamentals.^[1]

L'ús del concepte només es difongué amb el reconeixement d'efectes similars a la ressonància en sistemes acústics generals per part de John Strutt, Lord Rayleigh i Hermann von Helmholtz a la dècada de 1860, seguits d'experiments de William Thomson que demostren el comportament de ressonància natural dels circuits LC. El 1885, el físic alemany Anton Overbeck titulà un document sobre un fenomen amb oscil·lacions elèctriques similar a la ressonància, i fou el primer científic que registrà la famosa corba de ressonància, mostrant el voltatge excitat a diferents freqüències i el pic a causa de la interacció ressonant. Ben aviat, Heinrich Hertz relacionà aquests fenòmens de ressonància amb la generació d’ones electromagnètiques de propagació, i Guglielmo Marconi aviat els explotà per realitzar comunicacions sense fils. Però, tot plegat, es produí abans que els enginyers realment comencessin a apreciar el paper de la ressonància en sistemes mecànics més tangibles. L’acceptació gradual de la ressonància com a fenomen mecànic només es produí ja que els dramàtics fracassos en ponts i màquines van fer que els enginyers fossin conscients dolorosament de la inadequació de l’anàlisi estàtica de forces i de la necessitat de considerar els sorprenents efectes de les interaccions a freqüències similars.^[1]

El 1902, com a jove professor a Aquisgrà, Arnold Sommerfeld tingué un paper important en empènyer els enginyers a reconèixer la importància pràctica de la ressonància mecànica, llavors en gran part desconeguda. Realitzà un experiment amb una taula oscil·lant sobre la qual hi havia una màquina pesada. Augmentant la potència subministrada es podia fer funcionar la màquina més ràpidament, però només fins a un punt. A mesura que l’augment de la potència empenyia la màquina cada cop més ràpidament, aproximant-se a la freqüència de ressonància de la taula, els espectadors podien veure que l'energia addicional només feia vibrar la taula de manera més violenta. Sommerfeld indicà que això significaria un augment de la factura del combustible sense obtenir res més que el risc de danyar la màquina i l'edifici. El fenomen es conegué com a «efecte Sommerfeld».^[1]

Ressonància mecànica

Tractament teòric

En el cas d'una massa $m$ acoblada a una molla de constant elàstica $k$ que oscil·la en la direcció de l'eix Y, la 2a llei de Newton compleix la llei de Hooke (força recuperadora proporcional al desplaçament $y$ ) i es pot expressar com:

$m{\frac {d^{2}y}{dt^{2}}}=-ky$ La solució d'aquesta equació diferencial és: ${\textstyle y(t)=Acos(\omega _{0}t)}$ , que si hom la substitueix a l'equació anterior obté que la freqüència angular $\omega _{0}$ és constant i val:

$\omega _{0}={\sqrt {\frac {k}{m}}}$

Aquesta freqüència angular és la que adopta el sistema quan es deixa oscil·lar lliurament, només depèn de la molla mitjançant la seva constant elàstica i de la massa que duu acoblada, s'anomena freqüència natural del sistema.

Si hom aplica a aquesta molla una força externa periòdica ${\textstyle F_{e}=F\cos(\omega t)}$ es té un sistema oscil·lant forçat amb una força total ${\textstyle F_{T}=-ky+F\cos(\omega t)}$ . Aplicant novament la 2a llei de Newton resulta:

$m{\frac {d^{2}y}{dt^{2}}}=-ky+F\cos(\omega t)$

la qual solució és ${\textstyle y=A\cos(\omega t)}$ , que es pot substituir i operar per obtenir l'amplitud del moviment:

$A={\frac {F}{k-m\omega ^{2}}}$ i com que $k=m\omega _{0}^{2}$ s'obté:

$A={\frac {F}{m(\omega _{0}^{2}-\omega ^{2})}}$

Si la freqüència de la força externa és semblant a la freqüència natural del sistema, l'amplitud tendeix a l'infinit. A cada oscil·lació la molla acumula energia. A aquesta situació és al que s'anomena ressonància.^[2]

Exemples

En un món sotmès contínuament a forces oscil·lants les estructures elàstiques com ara finestres, ponts, edificis, etc., és factible que en molts casos la freqüència de les forces oscil·lants coincideixi amb alguna de les freqüències naturals de les estructures elàstiques provocant fenòmens de ressonància.

Ponts

Vídeo de la caiguda del pont de Tacoma Narrows

Quan desenes o centenars de soldats marxen donant cops rítmics de freqüència molt constant al pis, al creuar sobre un pont, que com s'ha assenyalat és una estructura elàstica amb les seves pròpies freqüències naturals de vibració, en cas que conservin la seva marxa compassada es corre el perill que la seva freqüència de cops -aproximadament d'1 Hz- coincideixi amb alguna de les freqüències naturals de el pont; cal prendre en compte a més que la força de l'cop col·lectiu pot arribar a magnituds de desenes de milers de newtons, per evitar aquest perill és que a les formacions de soldats se'ls ordena trencar la marxa quan creuen un pont. El 1831 el pont suspès de Broughton a Manchester caigué a causa del pas de setanta quatra homes marxant al pas.^[3] A Angers, Maine i Loira, França, el 1850 també col·lapsà un pont en suspensió quan hi passava un batalló de cinc-cents soldats de l'exercit francès. Moriren uns 200 d'ells.^[4] El 1940, el pont de Tacoma Narrows, a l'estat de Washington, EUA, colapsà per efecte de la ressonància produïda pel vent.^[5]

Vehicles

Les actuacions estan fets de moltes parts elàstiques, com ara el volant, la palanca de velocitats, els vidres de les finestres, etc .; de fet, quan al volant se li dona un cop, se sent immediatament la seva vibració; doncs bé, quan el motor genera vibracions que coincideixen amb la freqüència natural de vibració d'algunes d'aquestes parts succeeix el fenomen de ressonància; és per això que els dissenyadors de les carrosseries han de tenir en compte que la potent font de vibracions del motor no provoqui la coincidència amb les freqüències naturals dels diversos components dels vehicles.^[2]

Cos humà

El cos humà està conformat amb estructures elàstiques com són els ossos, i és així que en el món de la medicina laboral s'ha de cuidar que la freqüència de cops de màquines com els martells pneumàtics que trenquen les capes de paviment, no coincideixi amb la freqüència natural de algunes de les parts de l'estructura òssia. Quan el cos humà està sotmès a vibracions de baixa freqüència, aquest es mou com un tot, però a freqüències altes la resposta de el cos és específica; així de 4 a 12 Hz els malucs i els espatlles comencen a ressonar, entre 20 i 30 Hz és el crani el que ressona, a freqüències més altes de 60 a 90 Hz són els globus oculars els que poden entrar en ressonància.^[2]

Món animal

En el món animal es tenen també exemples molt bells de ressonància; per exemple les freqüències de aleteig dels mosquits mascles i les femelles són diferents. A l'espècie Aedes aegypti la millor freqüència de l’antena femenina ronda els 230 Hz; la del mascle ronda els 380 Hz, que correspon aproximadament a la freqüència fonamental dels sons de vol femení. Els pèls antenals dels mascles estan sintonitzats de manera ressonant a freqüències compreses entre els 2600 i els 3100 Hz aproximadament i, per tant, s’acoblen rígidament a l'eix flagel·lar i es mouen junts amb l'eix flagel·lar quan s’estimula a freqüències biològicament rellevants al voltant dels 380 Hz. A causa d’aquest acoblament rígid, les forces que actuen sobre els pèls es poden transmetre a l'eix i, per tant, a l’òrgan sensorial auditiu a la base del flagel, un procés que es proposa per millorar la sensibilitat acústica. De fet, la sensibilitat mecànica de l’antena masculina no només supera la sensibilitat de l’antena femenina, sinó també la de tots els altres receptors de moviment d’artròpodes estudiats fins ara.^[6]

Sismes

Un exemple molt dràstic dels efectes destructius que poden produir-se en cas de ressonància, es presenta quan una ciutat és afectada per un sisme; la ciutat és plena d'estructures elàstiques de gran escala, com com edificis i ponts; la freqüència dels sismes, és a dir, la freqüència amb què es mou el sòl, està per damunt de tot en el rang dels 0,5–2 Hz, són freqüències relativament baixes, però les grans masses dels edificis de més de 5 pisos d'alçada per la seva pròpia inèrcia tendeixen a tenir freqüències baixes i propicien per tant l'ocurrència del fenomen de ressonància. En aquest cas l'amplitud de les oscil·lacions mecàniques dels edificis tendeix a créixer tant en cada cicle que poden arribar a el punt de ruptura, tal com succeir amb molts edificis en el gran terratrèmol de la ciutat de Mèxic de 1985.^[2]

Ressonància acústica

La ressonància acústica és un fenomen en què un sistema acústic amplifica les ones sonores la freqüència de les quals coincideix amb una de les seves pròpies freqüències naturals de vibració. Pot produir-se a freqüències fora del rang de l'audició humana.

Un objecte de ressonància acústica sol tenir més d’una freqüència de ressonància, especialment en harmònics de ressonància més forta. Vibrarà fàcilment a aquestes freqüències i vibrarà amb menys intensitat a altres freqüències. La ressonància acústica és important per als constructors d’instruments, ja que la majoria d’instruments acústics utilitzen ressonadors o caixes de ressonància, com ara les cordes i el cos d’un violí, la longitud del tub d’una flauta i la forma d’una membrana de tambor. La ressonància acústica també és important per a l'oïda. Per exemple, la ressonància d'un element estructural rígid, anomenat membrana basilar dins de la còclea de l'oïda interna, permet que les cèl·lules ciliades de la membrana detectin el so.

Un cas molt conegut de ressonància és quan un o una cantant dirigeixen la seva veu cap a una copa de vidre; és aparent que la copa és una estructura elàstica que vibra a freqüències clarament recognoscibles per l'oïda humana, per tant, l'afinat sentit dels cantants s'entona amb aquests sons i llança contra la copa un so potent de la mateixa freqüència, amb això es formen a la copa ones estacionàries, i si la intensitat i la freqüència es mantenen el temps suficient, es produeix el fenomen de ressonància fins que la copa a causa de les seves intenses vibracions es trenca.^[2]

És una experiència comuna que quan s'escolta música dins d'una cambra, algunes vegades a l'aparèixer sons de freqüència molt baixa els vidres de les finestres comencen a vibrar violentament. Això passa, de forma natural, perquè hi ha un fenomen de ressonància, ja que en aquests casos la freqüència dels sons greus coincideix amb alguna de les freqüències naturals d'oscil·lació dels vidres de les finestres.^[2]

Ressonància elèctrica

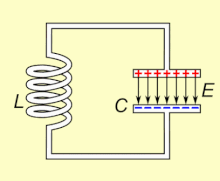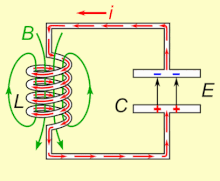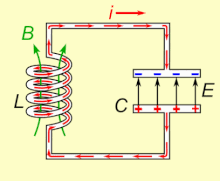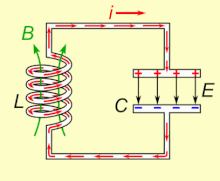
La ressonància elèctrica és un fenomen que es produeix en un circuit en el que existeixen elements reactius (bobines i condensadors) quan és recorregut per un corrent altern d'una freqüència tal que fa que la reactància s'anul·li, en cas d'estar tots dos en sèrie o es faça infinita si estan en paral·lel.

Un circuit LC o circuit ressonant és un circuit format per una bobina L i un condensador C. En circuit LC hi ha una freqüència per la qual es produeix un fenomen de ressonància elèctrica, a la qual es diu freqüència de ressonància, per la qual la reactància inductiva és igual a la reactància capacitiva. Per tant, la impedància serà mínima i igual a la resistència òhmica. Això també equival a dir, que el circuit estarà en fase.

Una característica dels circuits ressonants és que l'energia alliberada per un element reactiu (inductor o capacitor) és exactament igual a l'absorbida per l'altre. És a dir, durant la primera meitat d'un cicle d'entrada l'inductor absorbeix tota l'energia alliberada pel condensador, i durant la segona meitat del cicle el capacitor torna a capturar l'energia provinent de l'inductor. És precisament aquesta condició "oscil·latòria" que es coneix com a ressonància, i la freqüència en què aquesta condició es dona s'anomena freqüència ressonant.

Els circuits ressonants són especialment útils quan es vol fer "sintonitzadors" o "tuners", en els quals es vol donar prou potència a només una freqüència dins d'un espectre. Per exemple quan sintonitzem una emissora de ràdio en el nostre receptor el que s'ha produït és una condició de ressonància per a la freqüència central d'aquesta ràdio-emissora. En el cas dels receptors de ràdio comercials tenen un circuit ressonant "ajustable" per poder seleccionar la freqüència ressonant adequada.

Ressonància òptica

Una cavitat òptica, o ressonador òptic, és un dispositiu en el qual certs raigs lluminosos són susceptibles de restar confinats gràcies als miralls sobre els quals es reflecteixen. Aquestes cavitats són indispensables en els làsers perquè la seva llum passi moltes vegades en el seu medi amplificador. Són presents en els interferòmetres i dels oscil·ladors paramètrics òptics.

La manera més senzilla de realitzar una cavitat òptica és posar dos miralls plans o esfèrics cara a cara separats per una distància L. Es troba aquesta configuració en l'interferòmetre de Fabry-Pérot, i també en molts làsers de mida petita. Aquesta disposició no es pot utilitzar en material de mida grossa a causa de la dificultat d'aliniament (els miralls han d'estar paral·lels a alguns segons d'arc).

Amb dos miralls esfèrics de raigs de curvatura R₁ i R₂, es poden realitzar nombroses configuracions. Si els dos miralls tenen el mateix centre (R₁ + R₂ = L), es forma una cavitat concèntrica. Reemplaçant un dels dos miralls per un mirall pla posat al centre de l'altre, s'obté una cavitat hemisfèrica.

La cavitat confocal, és amb els dos miralls idèntics i els raigs de curvatura coincideixen amb la llargada de la cavitat (R₁ = R₂ = L). Aquest tipus permet produir els feixos el més fins possible.

Les cavitats còncaves-convexes estan constituïdes per dos miralls esfèrics : un de còncau i un de convex. Això permet de no focalitzar més els feixos, cosa important de vegades en els làsers de molta potència per a no destruir el medi amplificador.

Ressonància gravitacional

En mecànica celeste, es diu que hi ha ressonància orbital quan l'òrbita de dos cossos celestes tenen períodes de translació que, en ser dividits entre ells, el resultat és una fracció de nombres enters simples. Això significa que s'exerceixen una influència gravitatòria regular. Si el període orbital d'un satèl·lit és un múltiple exacte o una fracció del període d'un l'altre satèl·lit, l'efecte gravitatori net de cada satèl·lit sobre l'altre, ve a ser, en resum, una estirada o una empenta aplicat, repetidament, en el mateix punt del moviment cíclic. Així s'intensifica l'efecte. Això té un doble efecte: en alguns casos estabilitza i en altres desestabilitza les òrbites.

Exemples d'estabilització

Els períodes orbitals de Júpiter i Saturn estan en una ressonància 5:2. Això significa que per cada dues voltes que fa Saturn, Júpiter en fa cinc (i viceversa).

Plutó i alguns cossos més petits anomenats plutins, estan en ressonància 3:2 amb Neptú. Això significa que per cada tres voltes que fa Neptú, Plutó i alguns plutins en fan dos (i viceversa)

Els asteroides troians que ocupen els punts de Lagrange L₄ i L₅, i per tant, aquestes òrbites molt estables poden considerar-se en ressonància 1:1 amb Júpiter

La ressonància de Laplace fa que els períodes dels satèl·lits galileans de Júpiter (excepte Cal·listo) tinguin una relació entre els seus períodes orbitals de fraccions simples. Per exemple, els tres primers satèl·lits galileans Io, Europa i Ganimedes estan en una ressonància 4:2:1, respectivament.

En els satèl·lits de Saturn hi ha sis llunes amb ressonància orbital: El període de Mimas és 1/2 del de Tetis; el període de Encèlad és 1/2 del de Dione; el període d'Hiperió és 4/3 del de Tità.

Molts dels satèl·lits presenten una rotació síncrona, és a dir, triguen el mateix temps en girar sobre si mateixos, que quan giren al voltant del seu planeta. Es diu que estan en ressonància 1:1. Això significa que el satèl·lit mostra sempre la mateixa cara al planeta. L'exemple més comú és entre la Terra i la Lluna, però la immensa majoria dels satèl·lits estan en aquesta situació, entre ells tots els grans satèl·lits de Júpiter i Saturn. La raó és la força de marea, que ha detingut el gir del satèl·lit respecte al seu planeta. Perquè això ocorri, el satèl·lit ha de ser mínimament gran i estar relativament a prop del planeta

Exemples de desestabilització

La ressonància de Jupiter és responsable dels buits de Kirkwood o absència d'asteroides a determinades distàncies del cinturó d'asteroides que guarden una relació commensurable amb el període orbital de Júpiter. Els principals forats es troben a distàncies en els quals els asteroides trigarien a orbitar 1:3, 2:5, 3:7, i 1:2 del que triga Júpiter.

En els anells planetaris, i substancialment en els anells de Saturn, que són els més densos, prop de les distàncies radials del planeta a les que les partícules del disc tindrien un període orbital commensurat amb un dels satèl·lits del planeta (1/2, 1/3, 2/5) l'amplificació de l'efecte gravitatori del satèl·lits durant llargs períodes fa que es perdin partícules en una banda situada a la distància radial corresponent a una ressonància. L'explicació rau en el fet que cada nombre d'òrbites del satèl·lit natural, la partícula de l'anell dona voltes exactes, per la qual cosa al cap del temps en què el satèl·lit natural dona un nombre de voltes es troba a la mínima distància de la partícula, causant una estirada gravitatòria que fa que les òrbites de les partícules deixin de ser circulars, augmentant la possibilitat que les partícules desestabilitzades impactin amb les partícules estabilitzades.

Referències

↑ ^1,0 ^1,1 ^1,2 ^1,3 Buchanan, Mark «Going into resonance» (en anglès). Nature Physics, 15, 3, 3-2019, pàg. 203-203. DOI: 10.1038/s41567-019-0458-z. ISSN: 1745-2473.
↑ ^2,0 ^2,1 ^2,2 ^2,3 ^2,4 ^2,5 Peralta, J.A.; Reyes López, P.; Godínez Muñoz, A. «El fenómeno de la resonancia». Lat. Am. J. Phys. Educ. Vol. 3, No. 3, Sept. 2009, 3, 3, 9-2009, pàg. 612-618.
↑ Tietz, Tabea. «The Broughton Suspension Bridge and the Resonance Disaster» (en anglès americà), 12-04-2020. [Consulta: 31 juliol 2021].
↑ «Angers Bridge Collapse» (en anglès). [Consulta: 31 juliol 2021].
↑ Gazzola, Filippo. Brief History of Suspension Bridges. Cham: Springer International Publishing, 2015, p. 1–41. ISBN 978-3-319-15433-6.
↑ Gopfert, M.C.; Briegel, H.; Robert, D. «Mosquito hearing: sound-induced antennal vibrations in male and female Aedes aegypti». Journal of Experimental Biology, 202, 20, 15-10-1999, pàg. 2727–2738. DOI: 10.1242/jeb.202.20.2727. ISSN: 1477-9145.

[:0-1] 1,0 ^1,1 ^1,2 ^1,3 Buchanan, Mark «Going into resonance» (en anglès). Nature Physics, 15, 3, 3-2019, pàg. 203-203. DOI: 10.1038/s41567-019-0458-z. ISSN: 1745-2473.

[:1-2] 2,0 ^2,1 ^2,2 ^2,3 ^2,4 ^2,5 Peralta, J.A.; Reyes López, P.; Godínez Muñoz, A. «El fenómeno de la resonancia». Lat. Am. J. Phys. Educ. Vol. 3, No. 3, Sept. 2009, 3, 3, 9-2009, pàg. 612-618.

[3] Tietz, Tabea. «The Broughton Suspension Bridge and the Resonance Disaster» (en anglès americà), 12-04-2020. [Consulta: 31 juliol 2021].

[4] «Angers Bridge Collapse» (en anglès). [Consulta: 31 juliol 2021].

[5] Gazzola, Filippo. Brief History of Suspension Bridges. Cham: Springer International Publishing, 2015, p. 1–41. ISBN 978-3-319-15433-6.

[6] Gopfert, M.C.; Briegel, H.; Robert, D. «Mosquito hearing: sound-induced antennal vibrations in male and female Aedes aegypti». Journal of Experimental Biology, 202, 20, 15-10-1999, pàg. 2727–2738. DOI: 10.1242/jeb.202.20.2727. ISSN: 1477-9145.

[1]

[2]

[3]

[4]

[5]

[6]

Registres d'autoritat	BNF (1) GND (1) LCCN (1) NDL (1) NKC (1)
Bases d'informació	GEC (1)