Funció de dispersió de punt

Formació d'imatges en un microscopi confocal : tall longitudinal central (XZ). La distribució adquirida en 3D sorgeix de la convolució de les fonts de llum reals amb el PSF.

La funció de dispersió de punts (PSF) descriu la resposta d'un sistema d'imatge òptica enfocada a una font puntual o objecte puntual. Un terme més general per a la PSF és la resposta a l'impuls del sistema; el PSF és la resposta a impuls o funció de resposta a impuls (IRF) d'un sistema d'imatge òptica focalitzada. El PSF en molts contextos es pot considerar com la taca estesa en una imatge que representa un objecte puntual, que es considera com un impuls espacial. En termes funcionals, és la versió del domini espacial (és a dir, la transformada de Fourier inversa) de la funció de transferència òptica (OTF) d'un sistema d'imatge. És un concepte útil en òptica de Fourier, imatges astronòmiques, imatges mèdiques, microscòpia electrònica i altres tècniques d'imatge com ara la microscòpia 3D (com en la microscòpia d'exploració làser confocal) i la microscòpia de fluorescència.

Una font puntual tal com la representa un sistema amb una aberració esfèrica negativa (superior), zero (centre) i positiva (inferior). Les imatges de l'esquerra estan desenfocades cap a l'interior, les de la dreta cap a l'exterior.

El grau d'extensió (desenfocament) a la imatge d'un objecte puntual per a un sistema d'imatge és una mesura de la qualitat del sistema d'imatge. En sistemes d'imatge no coherents, com ara microscopis fluorescents, telescopis o microscopis òptics, el procés de formació de la imatge és lineal en la intensitat de la imatge i descrit per una teoria de sistemes lineals. Això vol dir que quan dos objectes A i B s'imatgen simultàniament per un sistema d'imatge no coherent, la imatge resultant és igual a la suma dels objectes amb imatges independents. En altres paraules: la imatge d'A no es veu afectada per la imatge de B i viceversa, a causa de la propietat de no interacció dels fotons. En els sistemes invariants a l'espai, és a dir, aquells en què la PSF és la mateixa a tot arreu de l'espai d'imatge, la imatge d'un objecte complex és llavors la convolució d'aquest objecte i la PSF. El PSF es pot derivar a partir de integrals de difracció.

Introducció

En virtut de la propietat de linealitat dels sistemes òptics d'imatges no coherents, és a dir,

Imatge (Objecte ₁ + Objecte₂) = Imatge (Objecte₁) + Imatge (Objecte₂)

la imatge d'un objecte en un microscopi o telescopi com a sistema d'imatge no coherent es pot calcular expressant el camp del pla objecte com una suma ponderada de funcions d'impuls 2D, i després expressant el camp del pla de la imatge com una suma ponderada de les imatges. d'aquestes funcions d'impuls. Això es coneix com el principi de superposició, vàlid per a sistemes lineals. Les imatges de les funcions d'impuls del pla objecte individuals s'anomenen funcions de dispersió de punts (PSF), que reflecteixen el fet que un punt matemàtic de llum en el pla objecte s'estén per formar una àrea finita en el pla de la imatge. (En algunes branques de les matemàtiques i la física, aquestes es podrien anomenar funcions de Green o funcions de resposta a impulsos. Els PSF es consideren funcions de resposta a impulsos per als sistemes d'imatge.

Aplicació de PSF: la desconvolució de la PSF modelada matemàticament i la imatge de baixa resolució millora la resolució.

Quan l'objecte es divideix en objectes puntuals discrets d'intensitat variable, la imatge es calcula com a suma de la PSF de cada punt. Com que el PSF normalment està determinat completament pel sistema d'imatge (és a dir, microscopi o telescopi), es pot descriure tota la imatge coneixent les propietats òptiques del sistema. Aquest procés d'imatge es formula normalment mitjançant una equació de convolució. En el processament d'imatges al microscopi i l'astronomia, conèixer el PSF del dispositiu de mesura és molt important per restaurar l'objecte (original) amb deconvolució. Per al cas dels raigs làser, el PSF es pot modelar matemàticament utilitzant els conceptes de feixos gaussians. Per exemple, la desconvolució del PSF modelat matemàticament i la imatge, millora la visibilitat de les característiques i elimina el soroll de la imatge.

Aplicacions

Microscòpia

Un exemple d'una funció de propagació de punts derivada experimentalment d'un microscopi confocal utilitzant un objectiu d'oli 63x 1,4NA. Es va generar mitjançant el programari de deconvolució Huygens Professional. Es mostren vistes en xz, xy, yz i una representació 3D.

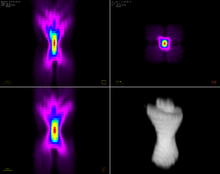
En microscòpia, la determinació experimental de PSF requereix fonts radiants de subresolució (puntuals). Els punts quàntics i les perles fluorescents solen considerar-se per a aquest propòsit. Els models teòrics descrits anteriorment, d'altra banda, permeten el càlcul detallat de la PSF per a diverses condicions d'imatge. Normalment es prefereix la forma limitada de difracció més compacta del PSF. Tanmateix, mitjançant l'ús d'elements òptics adequats (per exemple, un modulador de llum espacial), la forma del PSF es pot dissenyar per a diferents aplicacions.

Litografia

Pics de PSF superposats. Quan els pics estan tan a prop com ~ 1 longitud d'ona/NA, es fusionen efectivament. El FWHM és ~ 0,6 de longitud d'ona/NA en aquest punt.

El PSF també és un límit fonamental per a la imatge enfocada convencional d'un forat, amb la mida mínima impresa en el rang de 0,6-0,7 longitud d'ona/NA, sent NA l'obertura numèrica del sistema d'imatge. Per exemple, en el cas d'un sistema EUV amb una longitud d'ona de 13,5 nm i NA = 0,33, la mida mínima del forat individual que es pot visualitzar està en el rang de 25-29 nm. Una màscara de canvi de fase té vores de fase de 180 graus que permeten una resolució més fina.