Hidrodinàmica de partícules suavitzades
Aparença
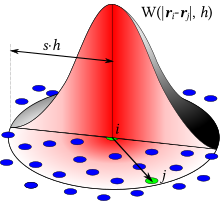
La hidrodinàmica de partícules suavitzades (SPH) és un mètode computacional utilitzat per simular la mecànica de medis continus, com ara la mecànica de sòlids i els fluxos de fluids. Va ser desenvolupat per Gingold i Monaghan [1] i Lucy [2] el 1977, inicialment per problemes astrofísics. S'ha utilitzat en molts camps d'investigació, incloent l'astrofísica, la balística, la vulcanologia i l'oceanografia. És un mètode lagrangià lliure de malla (on les coordenades es mouen amb el fluid) i la resolució del mètode es pot ajustar fàcilment respecte a variables com la densitat.[3]

Mètode
[modifica]Avantatges
[modifica]- Per construcció, SPH és un mètode lliure de malla, que el fa ideal per simular problemes dominats per dinàmiques de límits complexes, com ara fluxos de superfície lliure o grans desplaçaments de límits.
- La manca d'una malla simplifica significativament la implementació del model i la seva paral·lelització, fins i tot per a arquitectures de molts nuclis.
- SPH es pot estendre fàcilment a una gran varietat de camps i hibridar-se amb alguns altres models, tal com s'explica a Modeling Physics.
- Com es va comentar a la secció sobre SPH feblement compressible, el mètode té grans característiques de conservació.
- El cost computacional de les simulacions SPH per nombre de partícules és significativament menor que el cost de les simulacions basades en quadrícula per nombre de cel·les quan la mètrica d'interès està relacionada amb la densitat del fluid (per exemple, la funció de densitat de probabilitat de les fluctuacions de densitat). Aquest és el cas perquè a SPH la resolució es posa on està la qüestió.
Limitacions
[modifica]- Establir condicions de límit a SPH com ara entrades i sortides i parets és més difícil que amb mètodes basats en quadrícula. De fet, s'ha afirmat que "el tractament de les condicions de contorn és sens dubte un dels punts tècnics més difícils del mètode SPH". Aquest repte és en part perquè a SPH les partícules properes al límit canvien amb el temps. No obstant això, les condicions del límit de la paret per a SPH estan disponibles
- El cost computacional de les simulacions SPH per nombre de partícules és significativament més gran que el cost de les simulacions basades en quadrícula per nombre de cel·les quan la mètrica d'interès no està (directament) relacionada amb la densitat (per exemple, l'espectre d'energia cinètica). Per tant, sense tenir en compte els problemes d'acceleració paral·lela, la simulació de fluxos de densitat constant (per exemple, aerodinàmica externa) és més eficient amb mètodes basats en quadrícula que amb SPH.[5]
Referències
[modifica]- ↑ R.A. Gingold; J.J. Monaghan Mon. Not. R. Astron. Soc., 181, 3, 1977, pàg. 375–89. Bibcode: 1977MNRAS.181..375G. DOI: 10.1093/mnras/181.3.375 [Consulta: lliure].
- ↑ L.B. Lucy Astron. J., 82, 1977, pàg. 1013–1024. Bibcode: 1977AJ.....82.1013L. DOI: 10.1086/112164.
- ↑ Wang, Zhi-Bin; Chen, Rong; Wang, Hong; Liao, Qiang; Zhu, Xun «An overview of smoothed particle hydrodynamics for simulating multiphase flow». Applied Mathematical Modelling, 40, 23, 01-12-2016, pàg. 9625–9655. DOI: 10.1016/j.apm.2016.06.030. ISSN: 0307-904X.
- ↑ Colagrossi Computers and Fluids, 181, 2019, pàg. 345–363. DOI: 10.1016/j.compfluid.2019.01.007.
- ↑ Zhang, Chi; Zhu, Yu-jie; Wu, Dong; Adams, Nikolaus A.; Hu, Xiangyu «Smoothed particle hydrodynamics: Methodology development and recent achievement» (en anglès). Journal of Hydrodynamics, 34, 5, 01-10-2022, pàg. 767–805. DOI: 10.1007/s42241-022-0052-1. ISSN: 1878-0342.
