Johannes Robert Rydberg
| Biografia | |
|---|---|
| Naixement | 8 novembre 1854 Halmstad (Suècia) |
| Mort | 28 desembre 1919 parròquia de la catedral de Lund (Suècia) |
| Sepultura | Cementiri de Norra 55° 42′ 57″ N, 13° 11′ 29″ E / 55.71589°N,13.19139°E |
| Formació | Universitat de Lund |
| Activitat | |
| Camp de treball | Física |
| Ocupació | físic, professor d'universitat, matemàtic |
| Ocupador | Universitat de Lund (1880–1915) |
| Membre de | |
| Obra | |
Obres destacables | |
| Família | |
| Cònjuge | Lydia E. M. Carlsson |
| Pares | Maria Beata Andersson i Sven R. Rydberg |
| Premis | |
| |
Johannes Robert Rydberg (Halmstad, 8 de novembre de 1854 - parròquia de la catedral de Lund, 28 de desembre de 1919), també conegut com a Janne Rydberg, va ser un matemàtic i físic suec[1] destacat pels seus treballs en espectroscòpia, i conegut per haver desenvolupat, el 1888, una fórmula (la fórmula de Rydberg) que relaciona les longituds d'ona de les línies espectrals de certs elements de la Taula periòdica de Mendeleiev.[2]
Biografia
[modifica]Rydberg va néixer el 8 novembre 1854 a Halmstad. El seu pare, comerciant i petit armador, va morir quan ell tenia 4 anys, obligant la seva mare a viure amb pocs mitjans. Així i tot, va acabar els seus estudis, el batxillerat científic, a l'institut de Halmstad i va iniciar els estudis universitaris el 1873. Va començar a estudiar Matemàtiques i Física a la Universitat de Lund i va rebre el seu diploma dos anys més tard.[3] L'any 1879 va defensar la seva tesi doctoral titulada Construcció de seccions còniques amb 3 o 4 punts de contacte.[4] 1873 a la Universitat de Lund en la qual es va doctorar el 1879.[5]
Rydberg va començar la seva carrera com a instructor de treball pràctic a la Universitat de Lund. Va obtenir l'autorització per ensenyar matemàtiques el 1880 i física el 1882. Es va casar amb Eleonora Matilda Carlson el 1886. Van tenir dues filles i un fill.

La universitat de Lund es va convertir en el seu lloc de treball per tota la vida. Entre 1880 i 1882, com a professor de matemàtiques, va estudiar els problemes de l'electricitat per fricció. I així va esdevenir professor de física.[6] El 1901 va ser nomenat director del departament de física de la universitat.[5] El 1915 es va retirar i el 1916 va caure malalt i va ser ingressat a un hospital del qual ja no va sortir fins tres anys més tard en què va morir d'un vessament cerebral.[7][8]
Obra
[modifica]El seu treball de recerca més important, l'espectroscòpia, va estar motivat pel seu desig d'entendre la taula periòdica dels elements. Rydberg volia trobar l'expressió matemàtica que defineix les relacions de freqüència entre les diferents línies de l'espectre de cada element. El 1890 ho va aconseguir definint el concepte de nombre d'ona; la seva formulació expressa el nombre d'ona en termes d'una constant comuna a totes les sèries de línies de l'espectre.[6]
Observa que els pesos atòmics dels elements de la taula de Mendeleieff augmenten d'una manera aparentment irregular. Va començar a buscar una llei que regís la seva distribució.[9]
Aleshores es va interessar per les línies d'emissió o absorció espectral dels elements, pensant a trobar-hi la solució al seu problema.[9] El 1885, un matemàtic suís, Johann Jakob Balmer, va publicar una fórmula matemàtica per relacionar les longituds d'ona de les línies d'hidrogen en l'espectre visible.[10] Rydberg es va inspirar en la fórmula de Balmer per proposar el 1888 una nova manera de relacionar les línies espectrals, no només de l'hidrogen, sinó d'altres elements com els metalls alcalins.[11] Rydberg torna llavors a la seva investigació inútil sobre els pesos atòmics.[9]
El 1897, Rydberg va ser candidat per succeir a Karl Holmgren com a catedràtic de Física a la Universitat de Lund. Va ensenyar durant 15 anys com a ajudant de Holmgren. Entre els tres experts designats per jutjar la seva candidatura, dos van considerar poc interès la seva obra i un va jutjar que «El treball del doctor Rydberg sobre l'anàlisi d'espectres és, sens dubte, d'un gran valor científic i demostra la gran atenció i interès de l'autor pel tractament d'un problema sovint desagraït, però aquests treballs no poden establir plenament la seva competència per al càrrec en qüestió, atès que no es basen en les seves pròpies mesures i investigacions». Rydberg, però, té recomanacions de coneguts químics físics alemanys com Wilhelm Ostwald i Walther Nernst.[12]
Finalment, donada la seva creixent reputació internacional i després de la intervenció del rei Oscar II, Rydberg va ser nomenat professor el 1901 amb estatus especial. Per complementar el seu sou, va treballar a temps parcial com a expert digital a la Caixa d'estalvis de Lund el 1891 i com a actuari a Malmö el 1905.[4] El descobriment de noves sèries espectrals d'hidrogen per Theodor Lyman el 1906 i per Friedrich Paschen el 1908, sèrie que va satisfer la seva equació, va convèncer les autoritats acadèmiques sueques de la necessitat de nomenar Rydberg professor titular de física el 1909.[13]
Rydberg va descobrir una llei que explica les dades experimentals però sense conèixer el seu significat físic. Va ser Niels Bohr qui va justificar teòricament la fórmula de Rydberg el 1913 desenvolupant el seu model de l'àtom d'hidrogen. Malauradament, aquell mateix any, Rydberg va caure greument malalt. Primer ha de frenar les seves activitats, després aturar-se completament el 1915[9] Va morir el 28 desembre 1919. Manne Siegbahn, el seu antic alumne, el nomena[14] com a catedràtic de física a la Universitat de Lund.[4] Rydberg està enterrat al cementiri del nord de Lund. El van sobreviure la seva dona Lydia Carlsson (1856-1925), el seu fill Helge Rydberg (1887-1968) i la seva filla Gerda Rydberg (1891-1983).
Rydberg va romandre subestimat a Suècia malgrat la seva reputació internacional que va portar la Royal Society a donar-li la benvinguda com a membre estranger el 26 juny 1919. Si bé Rydberg no va rebre el Premi Nobel, Niels Bohr, en el seu discurs de recepció del Premi Nobel de Física el 1922, no va deixar de retre homenatge «al difunt professor Rydberg de Lund, el brillant treball del qual sobre les lleis espectrals va ser de gran importància per augmentar el nostre coneixement dels àtoms, i especialment per la contribució especial que vaig tenir el privilegi de fer».[15]
Fórmula de Rydberg
[modifica]
És conegut sobretot per haver ideat la fórmula de Rydberg el 1888 per predir les longituds d'ona dels fotons (de la llum o qualsevol radiació electromagnètica) emesos pels canvis en el nivell d'energia en un àtom.
La constant física coneguda com a constant de Rydberg rep el seu nom en el seu honor, igual que la unitat de Rydberg. Els àtoms excitats amb nombres quàntics principals molt alts, representats per n a la fórmula de Rydberg, s'anomenen àtoms de Rydberg, i un cràter de la Lluna també s'anomena Rydberg en el seu honor.
La teoria de Bohr, però, va demostrar, i més tard mesures més precises ho van confirmar, que la constant de Rydberg és una mica diferent de l'element químic i que el seu valor real és R per a un element donat:
Va ser membre de la Royal Society anglès: Royal Society) del 1919. Un cràter a la Lluna (cràter Rydberg) i un planetoide (10506 Rydberg) van rebre el seu nom.[16] Els àtoms excitats, amb nombres quàntics molt alts, que representen el nombre de la fórmula de Rydberg, s'anomenen àtoms de Rydberg. Les prediccions de Rydberg que les línies espectrals d'hidrogen, que s'obtenen a partir de la fórmula de Rydberg, ajudaran a la comprensió teòrica de l'estructura atòmica, es van utilitzar el 1913. N. Pi i va crear el model de l'àtom de Bohr. L'espectroscòpia utilitza una constant, que es basa en un àtom teòric de massa infinita, i s'anomena Rydberg en el seu honor.
on: - la càrrega elèctrica de l'electró, - la velocitat de la llum, - la constant de Planck.
És costum marcar les línies d'hidrogen amb les lletres inicials de l'alfabet grec, que vénen com a índexs del símbol químic. Els valors recíprocs de les longituds d'ona d'aquestes quatre línies estan donats per l'equació (fórmula de Rydberg)
Fets vivencials sobre espectres
[modifica]




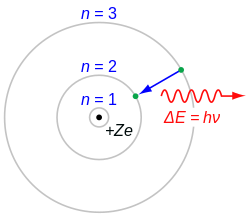




Els sòlids calents emeten llum amb longituds d'ona distribuïdes contínuament (radiació tèrmica). Quina part de l'espectre és la més forta (més intensa) depèn de la temperatura del cos brillant, però des del punt de màxima, la llum s'extingeix gradualment cap a longituds d'ona més curtes i més llargues. En contrast amb l'espectre continu dels cossos sòlids, s'observa una altra cosa en els gasos i el vapor. En el seu espectre apareixen línies discretes, que són característiques de certs elements químics. Tot l'espectre consta d'una sèrie de línies ben definides. És fàcil veure que l'espectre de línies prové dels àtoms. Aquests espectres s'obtenen durant experiments amb raigs catòdics i canals. Una descàrrega elèctrica en un tub de raigs catòdics de baixa pressió sempre fa que un gran nombre d'àtoms emetin llum. Els espectres de línies també són emesos pels gasos nobles, que consisteixen en àtoms purs, no en molècules. Els espectres de línia es poden estudiar en l' espectre d'emissió o d'absorció. Si s'emet llum blanca a través d'alguns vapors o gas, s'observa en l'espectre obtingut que es suprimeixen algunes longituds d'ona. Les línies fosques es troben exactament on es troben les línies d'emissió a l'espectre. Per tant, el gas absorbeix la llum d'aquelles longituds d'ona que d'altra manera emetria. L'espectre d'absorció coincideix completament amb l'espectre d'emissió. Aquesta determinació en l'espectre dels elements químics és una de les lleis fonamentals de la física nuclear.
Tot i que cada element químic té les seves pròpies línies espectrals especials, es poden observar algunes propietats comunes en els seus espectres, que ens permeten posar ordre al vast material espectroscòpic. Les línies espectrals de cada element químic es poden disposar en diverses sèries. Cada sèrie representa una sèrie de línies disposades segons una determinada regla. Sovint és obvi aprimera vista que les línies d'una sèrie pertanyen juntes. Si observeu les línies des de longituds d'ona més llargues fins a altres més curtes, es nota immediatament que la distància entre altres disminueix. Les línies s'amunteguen segons una determinada longitud d'ona, que és el límit d'aquesta sèrie.J. J. Balmer el 1885 va descobrir que l'espectre de l'hidrogen es pot representar mitjançant una equació matemàtica senzilla. Aleshores va ser conscient de 4 línies d'hidrogen visibles amb longituds d'ona.
Per raons que es presentaran més endavant, es va introduir que les equacions espectrals s'estableixen per a freqüències i no per a longituds d'ona. Els experiments, per descomptat, mesuren longituds d'ona (a partir de fenòmens d'interferència, difracció o dispersió), però les lleis de l'anàlisi espectral es fan més clares quan es tenen en compteles freqüències. Cal tenir en compte el següent: la freqüència ν es pot calcular a partir de la longitud d'ona λ segons la relació coneguda:
on: = 3, 4, 5, 6; i és l'anomenada constant de Rydberg. Si s'inclou a l'equació de Balmer per a nombres enters superiors a 7, s'obtenen longituds d'ona que es troben a la regió ultraviolada de l'espectre. De fet, els experiments han trobat unes 30 línies més que coincideixen completament amb l'equació de Balmer. Les línies s'apilen segons la longitud d'ona donada per l'expressió:
Aquest és el límit de la sèrie.
La sèrie Balmer és un tipus ideal de línies espectrals en general. Com es pot veure a la figura, la distància entre les línies adjacents disminueix correctament i les línies s'acumulen cap a un cert límit. Introduint la freqüència, l'equació de Balmer es pot escriure de la forma:
Però la velocitat de la llum no es mesura amb tanta precisió com ho són les mesures de longitud d'ona. La precisió de l'anàlisi espectral és insuperable. Per aquest motiu, totes les dades experimentals encara s'expressen en longituds d'ona en l'anàlisi espectral.
on = 3, 4, 5...
Per tant, les freqüències de les línies espectrals d'hidrogen es poden mostrar com a diferències (diferències) entre dos termes, el primer dels quals és constant i el segon disminueix com a 1/9, 1/16, 1/25, 1/36....
De seguida sorgeix la pregunta: s'ha de prendre sempre com a nombre constant 1/4? És possible pensar que el primer terme constant és qualsevol fracció. El 1908 Friedrich Paschen va trobar a la regió infraroja de les línies espectrals d'hidrogen les longituds d'ona de les quals coincideixen exactament amb les expressions:
Sèrie Liman:
- :
Hi ha, doncs, dos termes d'una sèrie, el terme constant de la qual és /3 ². Aquest terme també determina el límit de la sèrie. Es va trobar un nombre molt gran de línies de l'anomenada sèrie Paschen. El 1916 Lyman va trobar a l'altre costat de la sèrie de Balmer, a les profunditats de la regió ultraviolada, noves línies espectrals, que es poden representar amb la mateixa equació de Balmer, només que el terme constant del denominador hauria de ser el nombre sencer 1. L'espectre de l'hidrogen consta d'aquestes sèries: D'aquest gran nombre de línies, només les 4 primeres línies de la sèrie de Balmer cauen a la regió visible de l'espectre. Això mostra com és d'important examinar tot l'espectre per trobar les lleis bàsiques de la sèrie.
- on: m = 2, 3, 4.... Sèrie Ballmer:
- on: m = 3, 4, 5.... Sèrie Paschen:
- on: = 4, 5, 6.... Sèrie Brackett:
- on: m = 5, 6, 7.... Sèrie Pfund:
- on: m = 6, 7, 8.... Les freqüències de les líniesespectrals d'hidrogen generalment es poden expressar mitjançant l'equació: on: i - nombres enters.
- Les freqüències de les línies d'hidrogen s'obtenen, per tant, per fer totes les possibles diferències positives (diferències) de la seqüència. Així explicat, l'equació de Balmer ens porta al principi general de combinació, que va ser descobert per Walther Ritz el 1908. Segons aquest principi, es poden establir un nombre de membres per a cada element químic,.... de manera que les freqüències del seu espectre vénen donades per les diferències:
- El principi de combinació de Ritzes va confirmar en examinar tots els espectres. És la clau per ordenar les diferents sèries. El principi de combinació conté una llei bàsica de la naturalesa, que només es revela plenament a la física nuclear.[17]
Publicacions de Johannes Rydberg
[modifica]- Article ampliat: Johannes R. Rydberg «Investigació sobre la constitució dels espectres d'emissió d'elements químics». Kongliga Svenska Vetenskaps-Akademiens Handlingar [Actes de la Reial Acadèmia Sueca de Ciències], vol. 23, no 11, 1889, pàg. 1-177. Johannes R. Rydberg «Investigació sobre la constitució dels espectres d'emissió d'elements químics». Kongliga Svenska Vetenskaps-Akademiens Handlingar [Actes de la Reial Acadèmia Sueca de Ciències], vol. 23, no 11, 1889, pàg. 1-177.
- Nota resum Johannes R. Rydberg «On the structure of the line-spectra of the chemical elements» (en anglès). Philosophical Magazine, vol. 29, 1890, pàg. 331-337. Johannes R. Rydberg «On the structure of the line-spectra of the chemical elements» (en anglès). Philosophical Magazine, vol. 29, 1890, pàg. 331-337..
Referències
[modifica]- ↑ «Johannes Robert Rydberg | Swedish physicist». Encyclopedia Britannica. Arxivat de l'original el 2021-02-07. [Consulta: 2 febrer 2021].
- ↑ Šibalić, Nikola. Rydberg Physics. IOP Publishing, 2018. DOI 10.1088/978-0-7503-1635-4. ISBN 9780750316354.
- ↑ Hamilton, Paul Charles. Janne Rydberg: a physicist in 19th-century Sweden, 1992, p. 26–30.
- ↑ 4,0 4,1 4,2 Hamilton, Paul Charles. Janne Rydberg, 1992, p. 26–30.
- ↑ 5,0 5,1 Bigg, 2007, p. 999.
- ↑ 6,0 6,1 Leiter, 2003, p. 259.
- ↑ Martinson, I.; Curtis, L.J. «Còpia arxivada» (en anglès). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 235, 1–4, 2005, pàg. 17–22. Arxivat de l'original el 2023-08-30. Bibcode: 2005NIMPB.235...17M. DOI: 10.1016/j.nimb.2005.03.137 [Consulta: 5 juny 2024].
- ↑ Hamilton. Janne Rydberg: a physicist in 19th-century Sweden, 1992, p. 47–48.
- ↑ 9,0 9,1 9,2 9,3 Litzén, Ulf. Fysik i Lund under 300 år (en suec). Lunds universitetshistoriska sällskap, 2015, p. 71–75. ISBN 978-91-7545-320-0.
- ↑ Magie, William Francis. A Source Book in Physics. Harvard University Press, 1969, p. 360..
- ↑ Rydberg, 1889.
- ↑ «Mikes Sutton, Getting the numbers right - the lonely struggle of Rydberg» (en anglès). www.chemistryworld.com, 1er juliol 2004. [Consulta: 2 setembre 2019].[Enllaç no actiu]
- ↑ «Arvid Leide, Janne Rydberg och hans kamp för professuren» (en suédois). lup.lub.lu.se, 1954. Arxivat de l'original el 31 de maig 2020. [Consulta: 24 agost 2019].
- ↑ Martinson, I.; Curtis, L.J. «Janne Rydberg – his life and work» (en anglès). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 235, 1–4, 2005, pàg. 17–22. Bibcode: 2005NIMPB.235...17M. DOI: 10.1016/j.nimb.2005.03.137.
- ↑ Leide, Arvid «Janne Rydberg och hans kamp för professuren». Lund University Publications, 1954. Arxivat de l'original el 2020-05-31 [Consulta: 29 maig 2024].
- ↑ Rydberg, Johannes Robert , "Hrvatska enciklopedi-ja", Leksikografski zavod Miroslav Krleža, enciklopedija.hr, 2017.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb,1966.
Bibliografia
[modifica]- Bigg, Charlotte. «Rydberg, Johannes Robert». A: Hockey T. et al. (eds). Biographical Encyclopedia of Astronomers (en anglès). Springer, 2007, p. 998-999. ISBN 9780387304007.
- Leiter, Darryl J. «Rydberg, Johannes Robert». A: A to Z of Physicists (en anglès). Facts on File, 2003, p. 259-260. ISBN 0-8160-4798-7.
- Martinson, I.; Curtis, L.J. «Janne Rydberg – his life and work» (en anglès). Nuclear instruments and methods in physics research, Vol. 235, Num. 1-4, 2005, pàg. 17-22. DOI: 10.1016/j.nimb.2005.03.137. ISSN: 0168-583X.
Enllaços externs
[modifica]- O'Connor, John J.; Robertson, Edmund F. «Johannes Robert Rydberg» (en anglès). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland. (anglès)
- Maier, C.L. «Rydberg, Johannes (Janne) Robert». Complete Dictionary of Scientific Biography, 2008. [Consulta: 20 maig 2018]. (anglès)
















