Llei de Metcalfe

Dos telèfons només poden fer una connexió. Cinc, poden fer 10 connexions, i dotze poden fer 66 connexions.

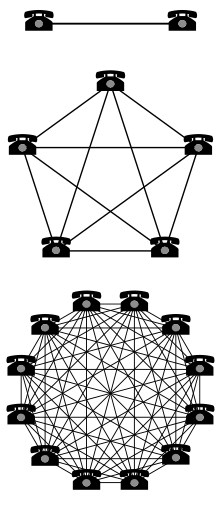
La llei de Metcalfe diu que el valor (utilitat) d'un sistema de comunicacions augmenta proporcionalment al quadrat del nombre d'usuaris del sistema (N²). Car un usuari no pot connectar-se amb ell mateix, la fórmula és:

N(N−1), o N²−N.

Formulada per primer cop per en Robert Metcalfe en relació amb l'Ethernet, la llei de Metcalfe explica molts dels efectes de xarxa de les tecnologies i xarxes de comunicacions, com Internet o la World Wide Web.

La llei sol il·lustrar-se amb l'exemple dels aparells de fax: un sol aparell de fax és inútil, però el valor de cada aparell de fax augmenta amb el nombre total de faxos a la xarxa, ja que el nombre total de gent que pot enviar i rebre documents creix. Això contrasta amb els models tradicionals de l'oferta i demanda on, si augmenta la quantitat d'alguna cosa, el seu valor disminueix.

Aplicacions

La llei de Metcalfe es pot aplicar tant a les telecomunicacions com a gairebé qualsevol sistema que intercanviï informació. Alguns exemples d'aquests sistemes son els telèfons, els fax, els sistemes operatius, les aplicacions de software i les xarxes socials.

Aquesta llei prediu si un producte o estàndard tendirà a dominar el mercat. Això té implicacions per les quals una solució innovadora pot introduir-se en un mercat o bé requereix altres interfícies.

Revisions

Hi ha hagut revisions posteriors al valor afegit estimat: la llei de Metcalfe exagera el benefici. Ja que un usuari no es pot connectar amb ell mateix, el càlcul es redueix al nombre d'artsites d'un graf complet de n vèrtexs.

${\frac {n(n-1)}{2}}$

El març de 2006, Andrew Odlyzko i Benjamin Tilly van publicar un esborrany d'un article que concloïa en que la Llei de Metcalfe sobreestimava significativament el valor de les connexions afegides. La regla diu que el valor d'una xarxa amb n nodes no es el quadrat de n sinó n vegades el logaritme d'n. La seva principal justificació és la idea que no totes les connexions potencials en una xarxa tenen el mateix valor. Per exemple, la majoria de persones truquen més sovint a la seva família que a un ciutadà d'un altre país. A l'IEEE Spectrium de juliol de 2006, Bob Briscoe, Odlyzko i TIlly afirmen que la llei de Metcalfe és errònia. El mateix Robert Metcalfe va respondre l'article defensant la seva llei.

Per altra banda, la llei de Reed demostra que la llei de Metcalfe menysvalora el valor de les connexions afegides. No només és un membre connectat a la xarxa com un tot, sinó que alhora a molts subconjunts d'aquest tot. Aquests subconjunts afegeixen valor independent de l'individu o la xarxa com un tot. Incloure els subconjunts en el càlcul del valor de la xarxa augmenta el seu valor en major velocitat que incloure només els nodes individuals.

Limitacions

A més de la dificultat de quantificar el valor d'una xarxa, la justificació matemàtica de la llei de Metcalfe només mesura el nombre potencial de contactes; el costat tecnològic d'una xarxa. Tanmateix, la utilitat social d'una xarxa depèn del nombre de nodes en contacte. Si hi ha barreres d'idiomes o altres raons per les quals gran part d'una xarxa no està en contracte, l'efecte pot ser menor.

La llei de Metcalfe dona per fet que el valor de cada node n és igual. Però si aquest no és el cas, el valor relatiu d'una connexió addicional disminueix. De la mateixa manera, a les xarxes socials, si els usuaris que s'acaben d'unir a aquestes utilitzen menys les xarxes que els usuaris que fa més temps que s'han unit, el benefici de cada usuari addicional pot disminuir, fent que la xarxa general sigui menys eficient si els costos per usuari són fixes.

Validació amb dades reals

Durant 30 anys no va haver-hi proves reals a favor o en contra de la llei de Metcalfe. No va ser fins al juliol de 2013 quan investigadors holandesos van aconseguir analitzar els patrons d'ús d'Internet a Europa durant un temps suficient i van trobar la proporcionalitat d'$n^{2}$ per valors petits d'n i la proporcionalitat (n log n) per valors grans d'n. Uns mesos després, Metcalfe va aportar proves addicionals: va utilitzar les dades de Facebook dels darrers deu anys per mostrar una bona adaptació a la llei de Metcalfe.

El 2015, Zhang, Liu i Xu van ampliar els resultats de Metcalfe mitjançant dades de Facebook i Tencent, la companyia de xarxes socials més gran de la Xina. El seu treball va demostrar que la llei de Metcalfe es mantenia per a tots dos, malgrat la diferència de públic entre els dos llocs; Facebook atén una audiència mundial i Tencent només serveix els usuaris xinesos. Les funcions de Metcalfe dels dos llocs eren les següents:

$V_{Tencent}=7.39\times 10^{-9}\times n^{2}$

$V_{Facebook}=5.70\times 10^{-9}\times n^{2}$

El 2018, Peterson va aplicar la llei de Metcalfe a la criptomoneda Bitcoin, i va demostrar que la llei de Metcalfe determinava més del 70% del valor de Bitcoin. En un treball encara no publicat, Peterson va proporcionar una derivació matemàtica que va relacionar conceptes tradicionals de valor de diners al valor de Metcalfe, i va utilitzar Bitcoin i Facebook com a exemples numèrics de la prova.