Llibertat asimptòtica

En física, la llibertat asimptòtica és una propietat d'algunes interaccions descrites per teories de gauge on la força entre partícules disminueix a mesura que la seva energia creix o, equivalentment, la seva separació disminueix. La interacció esdevé així asimptòticament nul·la i les partícules no interaccionen, sent "lliures".

Evolució de la "constant" d'acoblament de la QCD (interacció forta) α_s en funció de l'energia (Q). (Ref. Particle Data Group 2015)

La llibertat asimptòtica és una característica de la cromodinàmica quàntica (QCD), la teoria de quàntica de camps que descriu la interacció forta entre quarks i gluons, els constituents fonamentals de la matèria nuclear (protons i neutrons). La força d'acoblament de la QCD (α_s) disminueix amb l'energia i els quarks i gluons interaccionen més feblement quan més energètics són. Aquest fet permet realitzar càlculs teòrics pertorbatius de la QCD, mitjançant una expansió en potències d'α_s. Al contrari, a baixes energies (per sota d'1 GeV, la massa típica d'un protó) la interacció forta creix ràpidament, degut al confinament del color que porta a la formació d'estats lligats compostos de tres quarks (barions, com els protons o neutrons) o dos quarks (mesons, com els pions o kaons).

La llibertat asimptòtica de la QCD va ser descoberta el 1973 per Franc Wilczek i David Gross i, independentment, per David Politzer. Tot tres van compartir el premi Nobel de física el 2004 per aquest treball. La constant d'acoblament de la QCD decreix logarítmicament amb l'energia k com

$\alpha _{s}(k^{2})\ {\stackrel {\mathrm {def} }{=}}\ {\frac {g_{s}^{2}(k^{2})}{4\pi }}\approx {\frac {1}{\beta _{0}\ln(k^{2}/\Lambda ^{2})}},$

on β₀ és el primer terme de la funció-beta de la teoria i Λ≈200 MeV, anomenada escala de QCD, una constant indicant el valor de l'energia per la qual l'acoblament divergeix en càlculs pertorbatius.

Apantallament i antiapantallament del buit

Apantallament de càrrega elèctrica en la QED

La variació d'una constant d'acoblament en funció de l'energia pot ser entesa qualitativament com deguda a l'acció del camp de partícules virtuals que porten la càrrega corresponent a la interacció.

En el cas de la l'electrodinàmica quàntica (QED), el creixement de l'acoblament amb l'energia és conseqüència de l'apantallament degut a parelles partícula-antipartícula carregades, parells electró-positró en aquest cas, al buit. A prop d'una càrrega "central" donada, el buit esdevé polaritzat: partícules virtuals de càrrega oposada són atretes per la càrrega central, i partícules virtuals de la mateixa càrrega que la central són repel·lides. L'efecte net és una cancel·lació parcial del camp a qualsevol distància finita de la càrrega original. Apropant-se més i més a la càrrega central, hom veu cada vegada menys l'efecte del buit polaritzat i, per tant, un creixement de la càrrega central eficaç, que esdevé divergent quan la distància s'apropa a zero, l'anomenat pol de Landau.

Diagrames de polarització del buit en QCD que generen l'antiapantallament d'una càrrega de color donada, a altes energies.

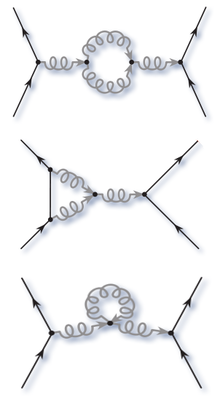
En el cas de la QCD el mateix fenomen té lloc amb parelles virtuals quark-antiquark que tendeixen a apantallar la càrrega de color d'un quark central donat. Tanmateix, la QCD es caracteritza per un detall addicional molt diferent: els bosons portadors de la força, els gluons, són ells també portadors de càrrega de color (a diferència dels fotons de la QED que són neutres). De fet, cada gluó porta dues càrregues de color. L'efecte net de polarització del buit degut als gluons virtuals no condueix a un apantallament del camp, sinó a una augmentació acompanyada d'un canvi de color. Aquest fenomen s'anomena antiapantallament perquè quan hom s'apropa més i més a un quark donat, el núvol de gluons virtuals circumdants disminueix la càrrega eficaç central.

Donat que els quarks i gluons virtuals contribueixen amb efectes oposats, l'efecte net final depén del nombre de tipus diferents (sabors) de quarks. Per a la QCD estàndard amb tres colors i sempre que no n'hi hagi més de 16 sabors de quarks (sense comptar separadament els antiquarks), l'antiapantallament preval i la teoria és asimptòticament lliure. Aquest sembla el cas realitzat a la natura, car només existeixen 6 sabors de quarks coneguts.

La funció-beta i la llibertat asimptòtica de la QCD

La llibertat asimptòtica pot ser derivada a partir de la funció-beta que descriu la variació de la constant d'acoblament de la teoria en el marc d'un grup de renormalitzacio donat. Per distàncies prou curtes o, equivalentment, per grans intercanvis de moment amb alt "poder de resolució" (donada la relació inversa entre moment i longitud d'ona), una teoria asimptòticament lliure és susceptible de ser calculada a partir d'una expansió pertorbativa utilitzat diagrames de Feynman. Aquestes situacions són més tractables teòricament que el cas invers de llarga-distància o acoblament-fort, present també en aquestes teories, que genera el confinament.

Per calcular la funció-beta cal avaluar els diagrames de Feynman que contribueixen a la interacció d'un quark emetent o absorbint un gluó. Essencialment, la funció beta descriu la variació de la constant d'acoblament quan hom escala el sistema $x\rightarrow bx$. El càlcul es pot fer rescalant a l'espai de posicions o a l'espai de moments. En el cas de teories de gauge no-abelianes com la QCD, l'existència de llibertat asimptòtica depén del grup de gauge i del nombre de sabors de les partícules interactuants. A l'ordre més baix no trivial, la funció-beta en una teoria de gauge SU(N) amb n_f sabors de quarks, és

$\beta _{1}(\alpha )={\alpha ^{2} \over \pi }\left(-{11N \over 6}+{n_{f} \over 3}\right)$

on α = g²/(4π) és l'equivalent de la constant d'estructura fina de la teoria (una versió normalitzada de l'acoblament de la QCD, g, típica en física de partícules). Si aquesta funció és negativa, la teoria és asimptòticament lliure. Per SU(N) amb N=3, el requisit $\beta _{1}<0$ dona:

$n_{f}<{33 \over 2}.$

Per això, la QCD és asimptòticament lliure si hi ha n_f=16 o menys sabors de quarks.

Al marge de la QCD, la llibertat asimptòtica pot ser present en altres sistemes com el model-sigma no-lineal en 2 dimensions, que té una estructura similar a la teoria de Yang-Mills invariant SU(N) en 4 dimensions.

Vegeu també

• Confinament de color
• Vincle químic