Moment magnètic anòmal

En electrodinàmica quàntica, el moment magnètic anòmal d'una partícula és una contribució dels efectes de la mecànica quàntica, expressats per diagrames de Feynman amb bucles, al moment magnètic d'aquesta partícula. (El moment magnètic, també anomenat moment dipolar magnètic, és una mesura de la força d'una font magnètica).

Correcció d'un sol bucle al moment dipolar magnètic d' un fermió.

El moment magnètic "Dirac", corresponent als diagrames de Feynman a nivell d'arbre (que es pot considerar com el resultat clàssic), es pot calcular a partir de l'equació de Dirac. Normalment s'expressa en termes del factor g; prediu l'equació de Dirac $g=2$ . Per a partícules com l'electró, aquest resultat clàssic difereix del valor observat en una petita fracció d'un percentatge. La diferència és el moment magnètic anòmal, indicat $a$ i es defineix com$$a={\frac {g-2}{2}}$$

Electró

La contribució d'un sol bucle al moment magnètic anòmal —corresponent a la primera i més gran correcció mecànica quàntica— de l'electró es troba calculant la funció de vèrtex que es mostra al diagrama adjacent. El càlcul és relativament senzill  i el resultat d'un sol bucle és:$$a_{\text{e}}={\frac {\alpha }{2\pi }}\approx 0.001\,161\,4,$$on $\alpha$ és la constant d'estructura fina. Aquest resultat va ser trobat per primera vegada per Julian Schwinger el 1948  i està gravat a la seva làpida. A partir de 2016, els coeficients de la fórmula QED per al moment magnètic anòmal de l'electró es coneixen analíticament fins a $\alpha ^{3}$  i s'han calculat per encàrrec $\alpha ^{5}$: $$a_{\text{e}}=0.001\,159\,652\,181\,643(764)$$La predicció QED coincideix amb el valor mesurat experimentalment a més de 10 xifres significatives, fent que el moment magnètic de l'electró sigui la predicció verificada amb més precisió de la història de la física. (Consulteu Proves de precisió de QED per obtenir més informació). El valor experimental i la incertesa actuals són: $$a_{\text{e}}=0.001\,159\,652\,180\,59(13)$$Segons aquest valor, $a_{\text{e}}$ es coneix amb una precisió d'aproximadament 1 part en 10 mil milions (10¹⁰). Això requeria mesurar $g$ amb una precisió d'aproximadament 1 part en 10 bilions (10¹³).

Muon

Correccions d'un sol bucle del model estàndard supersimètric mínim proposades al muó g −2 que impliquen partícules més enllà del model estàndard: un neutralino i un smuon, i un chargino i un sneutrí muó respectivament.

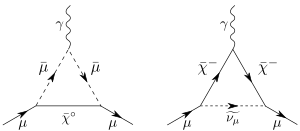
El moment magnètic anòmal del muó es calcula de manera similar a l'electró. La predicció del valor del moment magnètic anòmal del muó inclou tres parts: $${\begin{aligned}a_{\mu }^{\mathrm {SM} }&=a_{\mu }^{\mathrm {QED} }+a_{\mu }^{\mathrm {EW} }+a_{\mu }^{\mathrm {hadron} }\\&=0.001\,165\,918\,04(51)\end{aligned}}$$Dels dos primers components, $a_{\mu }^{\mathrm {QED} }$ representa els bucles de fotons i leptons, i $a_{\mu }^{\mathrm {EW} }$ la W bosó, bosó de Higgs i Z bucles de bosons; tots dos es poden calcular amb precisió a partir dels primers principis. El tercer terme, $a_{\mu }^{\mathrm {hadron} }$, representa bucles hadrons; no es pot calcular amb precisió només a partir de la teoria. S'estima a partir de mesures experimentals de la relació de seccions transversals hadròniques i muòniques (R) en col·lisions electró - antielectró (e ⁻ –e ⁺). A partir de juliol 2017, la mesura no està d'acord amb el model estàndard per 3,5 les desviacions estàndard suggereixen que la física més enllà del model estàndard pot tenir un efecte (o que els errors teòrics/experimentals no estan completament controlats). Aquesta és una de les discrepàncies de llarga data entre el model estàndard i l'experiment.

Tau

La predicció del model estàndard per al moment dipolar magnètic anòmal de tau és $$a_{\tau }=0.001\,177\,21(5),$$mentre que el millor mesurat anava a $a_{\tau }$ és $$-0.052<a_{\tau }<+0.013.$$