Moviment rectilini uniformement accelerat

En física, el moviment rectilini uniformement accelerat (MRUA), també conegut com a moviment rectilini uniformement variat (MRUV), és aquell en el qual un mòbil es desplaça sobre una trajectòria recta estant sotmès a una acceleració constant.

Un exemple d'aquest tipus de moviment és la caiguda lliure vertical, en el qual l'acceleració que hi intervé, i considerada constant, és la que correspon a la gravetat.

Des del punt de vista de la dinàmica, també pot definir-se com el moviment que realitza una partícula que partint del repòs és accelerada per una força constant.

El Moviment Rectilini Uniformement Accelerat (MRUA) és un cas particular del moviment uniformement accelerat (MUA).

Moviment rectilini uniformement accelerat en mecànica "newtoniana"

En mecànica clàssica el moviment rectilini uniformement accelerat (MRUA) presenta dues característiques fonamentals:

1. La trajectòria és rectilínia
2. L'acceleració sobre la partícula és constant

A partir de la segona Llei de Newton es pot expressar:

$\mathbf {F} =m\,\mathbf {a}$

Atès que la massa és una constant, si la força resultant aplicada és constant resultarà que l'acceleració també serà constant.

Per tant, això determina que:

1. La velocitat varia linealment respecte del temps.
2. La posició varia segons una relació quadràtica respecte del temps.

L’acceleració constant es veu com una línia horitzontal, cosa que vol dir que no canvia. Això provoca que la velocitat augmenti de manera lineal, representada per una línia amb pendent. A mesura que la velocitat creix, el desplaçament comença a canviar en forma de paràbola. Al principi, el desplaçament és lent, però després, quan la velocitat augmenta, comença a créixer més ràpidament.

En resum, una acceleració constant provoca un augment lineal de la velocitat, que fa que el desplaçament canviï de manera quadràtica.

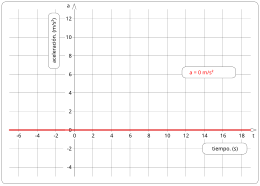
L'acceleració a constant, en l'exemple:

$a=a_{0}$

podem veure la gràfica de la funció de l'acceleració respecte al temps, es veu clarament que són rectes horitzontals.

La velocitat v per a un instant t donat és:

$v(t)=at+v_{0}$

Per a una mateixa velocitat inicial amb diferents acceleracions tenim un feix de rectes de diferent pendent:

amb una mateixa acceleració i diferents velocitats inicials tenim rectes paral·leles com les dels gràfics:

Finalment la posició en funció del temps s'expressa per:

$e(t)={\frac {1}{2}}at^{2}+v_{0}t+e_{0}$

On $e_{0}\,$ és la posició inicial.

La funció de la posició respecte al temps, quan l'acceleració és constant i diferent de zero, forma una paràbola. Si mantenim fixa la velocitat inicial i la posició inicial, veurem que, amb diferents acceleracions, es creen paràboles que passen pel mateix punt i tenen el mateix pendent al principi.

Això significa que, tot i que les formes de les paràboles varien, totes arriben al mateix punt inicial. Una acceleració més gran fa que la corba sigui més pronunciada. És fascinant com, amb canvis en l'acceleració, podem observar com es comporten els moviments de manera tan diferent, però amb un inici comú.