Octets d'hadrons

L'octet dels mesons pseudoescalars. Les partícules al llarg d'una mateixa línia horitzontal comparteixen la mateixa estranyesa, s, mentre que les de les mateixes diagonals inclinades a l'esquerra comparteixen la mateixa càrrega, q (expressada en múltiples de la càrrega elemental).

En física, els octets d'hadrons són esquemes organitzatius utilitzats per a ordenar els diferents hadrons segons els seus nombres quàntics, i que van contribuir al desenvolupament del model de quarks. La idea va ser proposada simultàniament per Murray Gell-Mann i Yuval Ne'eman de forma independent l'any 1961.

Context

Fins a l'any 1947, es creia generalment des de la comunitat física que es tenia ja una bona comprensió de les partícules més elementals. Hi havia principalment electrons, protons, neutrons i fotons, i a més algunes partícules exòtiques inestables (és a dir, que es desintegren radioactivament) necessàries per explicar les observacions de raigs còsmics, com els pions, muons i els neutrins, aquests últims encara una hipòtesi. A més, el descobriment del positró suggeria que podrien existir antipartícules per a cadascun d'ells. Se sabia que havia d'existir una interacció forta per superar la repulsió electroestàtica als nuclis atòmics, i aquesta interaccionava només amb algunes partícules. Les que ho fan, es van anomenar "hadrons", i aquests alhora es van classificar com a mesons (massa mitjana) i barions (major massa).

El descobriment del kaó neutre a finals de 1947 i el posterior descobriment d'un kaó de càrrega positiva el 1949 van ampliar la família dels mesons d'una manera inesperada, i el 1950 va passar el mateix amb la partícula lambda per a la família dels barions. Aquestes partícules es desintegren molt més lentament del que es produeixen, una indicació que hi ha dos processos físics diferents implicats. Aquesta teoria va ser suggerida per primera vegada per Abraham Pais el 1952. L'any 1953, Murray Gell-Mann i una col·laboració al Japó de Tadao Nakano amb Kazuhiko Nishijima, van suggerir de manera independent que existia un nou valor conservat conegut ara com a "estranyesa" durant els seus intents d'entendre el creixent nombre de partícules conegudes. El descobriment de nous mesons i barions va continuar durant la dècada de 1950 i el nombre de partícules "elementals" conegudes creixia ràpidament. Els físics estaven interessats a entendre les interaccions entre hadrons mitjançant la interacció forta. El concepte d'⁣isospin, introduït l'any 1932 per Werner Heisenberg poc després del descobriment del neutró, es va utilitzar per agrupar alguns hadrons en "multiplets", però cap teoria científica reeixida cobria els hadrons en el seu conjunt. Aquest va ser l'inici d'un període caòtic en la física de partícules que informalment es coneix com l'era del "zoo de partícules". Els octets d'hadrons van representar un pas per sortir d'aquesta confusió i dirigir-se cap al model de quarks, que va resultar ser la solució.

Organització

La teoria de representació de grups és la base matemàtica de la classificació en octets, però no és necessari entrar en detall amb la teoria per entendre com ajuda a organitzar les partícules. Les partícules es classifiquen primer en mesons i barions. Dins de cada grup, també es poden separar segons el seu moment angular de spin. Els patrons simètrics apareixen quan d'aquests grups de partícules se'n dibuixa la seva estranyesa representada en funció de la càrrega elèctrica. (Originalment, els físics van utilitzar un parell de propietats equivalents anomenades hipercàrrega i espín isotòpic, el darrer dels quals ara es coneix com a isoespín). La simetria d'aquests patrons és un indici de la simetria subjacent en la interacció forta entre les mateixes partícules.

Mesons

Originàriament, es van organitzar els mesons en octets i singlets. Aquesta classificació va servir com a inspiració per a classificar els mesons en grups de nou partícules en el model de quarks.

Octet de mesons

L'octet de mesons pseudoescalars.

Els primers mesons pseudoescalars (de spin 0) s'organitzen en un octet format per:

• Els kaons $K^{0}$, $K^{+}$, $K^{-}$ i ${\bar {K}}^{0}$.
• Els pions $\pi ^{+}$, $\pi ^{0}$ i $\pi ^{-}$.
• El mesó η.

Les partícules diametralment oposades en el diagrama són antipartícules entre si, mentre que les del centre són la seva pròpia antipartícula.

Mesó singlet

El mesó sense càrrega ni estranyesa $\eta '$ es va classificar originalment com a un grup separat, formant un singlet.

Barions

Octet bariònic

L'octet bariònic, amb J = 1/ 2 .

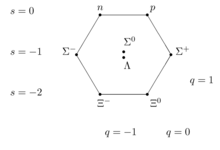
El sistema d'octets agrupa els següents barions de spin 1/2:

• El neutró (n) i el protó (p)
• Els barions sigma $\Sigma ^{-}$, $\Sigma ^{0}$ i $\Sigma ^{+}$.
• El barió lambda $\Lambda ^{0}$.
• Els barions xi $\Xi ^{-}$, $\Xi ^{0}$.

Decuplet bariònic

El decuplet bariònic, amb J = 3/ 2 .

Aquestes regles d'organització també es poden aplicar als barions amb spin 3/2, formant un decuplet o grup de deu:

• Els barions delta $\Delta ^{-}$, $\Delta ^{0}$, $\Delta ^{+}$ i $\Delta ^{++}$.
• Els barions sigma $\Sigma ^{*-}$, $\Sigma ^{*0}$ i $\Sigma ^{*+}$.
• Els barions xi $\Xi ^{*-}$, $\Xi ^{*0}$.
• El barió omega $\Omega ^{-}$.

De les partícules del decuplet, el barió $\Omega ^{-}$ encara no havia estat observat anteriorment quan es va proposar aquesta classificació. Gell-Mann va predir el 1962 que tindria una estranyesa de –3, càrrega elèctrica –1 i una massa al voltant de 1.680 MeV/c². L'any 1964, un grup d'investigació del Brookhaven National Laboratory va descobrir una partícula que coincidia amb aquestes propietats. Gell-Mann va rebre el Premi Nobel de Física l'any 1969 pel seu treball sobre la teoria de les partícules elementals.

Desenvolupament històric

Històricament, els quarks van ser postulats per entendre la simetria de sabor. En primer lloc, es va observar el 1961 que els grups de partícules estan relacionats entre si d'una manera que coincideix amb la teoria de representació de SU(3), indicant que es tracta d'una simetria de l'univers. Posteriorment, l'any 1964 això va portar al descobriment dels tres quarks lleugers (u, d i s), simètrics sota aquestes transformacions SU(3).

Interpretació moderna

Els octets d'hadrons es poden entendre en termes moderns com a una conseqüència de les simetries de sabor entre els diferents tipus de quarks. Ja que la força nuclear forta afecta els quarks de la mateixa manera independentment del seu sabor, substituir un sabor de quark per un altre en un hadró no hauria d'alterar substancialment la seva massa. Això es compleix sempre que les masses respectives dels quarks siguin més petites que l'escala de la interacció forta, fet que compleixen els tres quarks lleugers. Matemàticament, aquesta substitució es pot descriure amb elements del grup SU(3). Els octets i altres arranjaments d'hadrons són representacions d'aquest grup.

Simetria de sabor

SU(3)

Tenim un espai vectorial tridimensional abstracte:

$${\text{u}}\rightarrow {\begin{pmatrix}1\\0\\0\end{pmatrix}},\qquad {\text{d}}\rightarrow {\begin{pmatrix}0\\1\\0\end{pmatrix}},\qquad {\text{s}}\rightarrow {\begin{pmatrix}0\\0\\1\end{pmatrix}}$$

S'observa que les lleis de la física són aproximadament invariants sota una transformació unitària $A$ en aquest espai (a vegades anomenada rotació de sabor):

$${\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto A{\begin{pmatrix}x\\y\\z\end{pmatrix}},\quad A\in SU(3)$$

SU(3) es refereix al grup de Lie de matrius unitàries 3×3 amb determinant 1 (grup unitari especial). Per exemple, la rotació de sabor

$$A={\begin{pmatrix}~\;~0&1&0\\-1&0&0\\~\;~0&0&1\end{pmatrix}}$$

és una transformació que converteix simultàniament tots els quarks u de l'univers en quarks d i viceversa. Més concretament, aquestes rotacions de sabor són simetries exactes si només es consideren les interaccions fortes, però no són realment simetries exactes de l'univers perquè els tres quarks tenen diferents masses i diferents interaccions electrofebles.

Aquesta simetria aproximada s'anomena simetria de sabor, o més específicament, simetria de sabor SU(3).

Connexió amb la teoria de representacions

Suposem que tenim una partícula determinada, per exemple, un protó, en estat quàntic $|\psi \rangle$. Si apliquem una de les rotacions de sabor $A$ a la nostra partícula, aquesta entra en un nou estat quàntic que podem anomenar $A|\psi \rangle$. Depenent de $A$, aquest nou estat podria ser un protó, o un neutró, o una superposició d'un protó i un neutró, o diverses altres possibilitats. El conjunt de tots els estats quàntics possibles abasta un espai vectorial.

La teoria de la representació és una teoria matemàtica que descriu la situació en què els elements d'un grup (que serien les rotacions de sabor $A$ del grup SU(3)) són automorfismes d'un espai vectorial (en aquest cas, el conjunt de tots els estats quàntics possibles que s'obté d'aplicar una rotació de sabor a un protó). Per tant, estudiant la teoria de la representació de SU(3), es pot saber com podria ser l'espai vectorial i com es veurà afectat per la simetria de sabor.

Com que les rotacions de sabor $A$ són simetries aproximades, no exactes, cada estat ortogonal de l'espai vectorial correspon a una espècie de partícules diferent. A l'exemple anterior, quan un protó es transforma per totes les possibles rotacions de sabor $A$, resulta que es mou al voltant d'un espai vectorial de 8 dimensions. Aquestes 8 dimensions corresponen a les 8 partícules de l'octet bariònic (protó, neutró, $\Sigma ^{-}$, $\Sigma ^{0}$, $\Sigma ^{+}$, $\Xi ^{-}$, $\Xi ^{0}$ i $\Lambda$). Això correspon a una representació de 8 dimensions del grup SU(3). Com que $A$ és una simetria aproximada, totes les partícules d'aquest octet tenen massa similar.

Cada grup de Lie té una àlgebra de Lie corresponent, i cada representació de grup del grup de Lie es pot associar a una representació d'àlgebra de Lie corresponent al mateix espai vectorial. L'àlgebra de Lie ${\mathfrak {su}}$(3) es pot representar com el conjunt de matrius hermítiques 3×3 de traça 0. Normalment, s'estudia la teoria de la representació de l'àlgebra de Lie ${\mathfrak {su}}$(3) en comptes del grup de Lie SU(3), ja que el primer és més simple i ambdós són essencialment equivalents.