Operació bit a bit

Una operació bit a bit (en anglès bitwise operation) opera sobre nombres binaris a nivell dels seus bits individuals. És una acció primitiva ràpida i és suportada directament pels processador. En processadors simples de baix cost, les operacions de bit a bit, juntament amb els d'addició i subtracció, són substancialment més ràpides que la multiplicació i la divisió, mentre que en els moderns processadors d'alt rendiment usualment les operacions es realitzen a la mateixa velocitat.

Tipus d'operacions

Es poden distingir fins a tres tipus diferents d'operacions a nivell de bit:

Operacions bit a bit: Executen les operacions lògiques AND, OR, XOR, NOT, etc., sobre els bits individuals dels operands.
Operacions de desplaçament: Desplacen els bits dels operands cap a la dreta o cap a l'esquerra una o més posicions.
Operacions de rotació: Roten els bits de l'operand cap a la dreta o cap a l'esquerra una o més posicions. Es pot, o no, usar el flag de ròssec com un bit addicional en la rotació.

Operacions bit a bit

NOT

El NOT bit a bit, o bitwise, o complement, és una operació unaria que realitza la negació lògica a cada bit, invertint els bits del nombre, de tal manera que els zeros es converteixen en 1 i viceversa. Per exemple:

NOT 0111 (decimal 7)
= 1000 (decimal 8)

El NOT forma el complement a u d'un valor binari donat.

En un nombre enter amb signe en complement a dos, el NOT dona com a resultat l'invers additiu del nombre menys 1, és a dir NOT x =-x - 1 . Per obtenir el complement a dos d'un nombre, s'ha de sumar 1 al resultat, donant el negatiu del nombre. Això equival a un canvi de signe del nombre: +5 esdevé -5, i -5 esdevé +5.
Per als sencers sense signe, el complement bit a bit és la "reflexió de mirall" del nombre a través del punt mitjà del rang del sencer. Per exemple, per als enters sense signe de 8 bits, NOT x = 255 - x , per als enters sense signe de 16 bits, NOT x = 65535 - x , i en general, per als enters sense signe de n bits, NOT x = (2 ⁿ - 1) - x .

AND

El AND bit a bit, o bitwise, presa dos nombres enters i realitza l'operació AND lògica a cada parell corresponent de bits. El resultat en cada posició és 1 si el bit corresponent dels dos operands és 1, i 0 en cas contrari, per exemple:

0101 (decimal 5)
AND 0011 (decimal 3)
= 0001 (decimal 1)

El AND pot ser usat per filtrar determinats bits, permetent que uns bits passin i els altres no.

OR

Una operació OR de bit a bit, o bitwise, presa dos nombres enters i realitza l'operació OR inclusiu a cada parell corresponent de bits. El resultat en cada posició és 1 si el bit corresponent d'una dels dos operands és 1, i 0 si tots dos bits són 0, per exemple:

0101
OR 0011
= 0111

XOR

El XOR bit a bit, o bitwise, presa dos nombres enters i realitza l'operació OR exclusiu a cada parell corresponent de bits. El resultat en cada posició és 1 si el parell de bits són diferents i zero si el parell de bits són iguals.

0101
XOR 0011
= 0110

Operacions de desplaçament

Les operacions de desplaçament i rotació són:

Desplaçament lògic
Desplaçament aritmètic
Rotació
Rotació a través del bit de ròssec

Desplaçaments de bits

Els desplaçaments de bit (bitshifts) són de vegades considerats operacions bit a bit, perquè operen en la representació binària d'un nombre enter en lloc de sobre el seu valor numèric, però, els desplaçaments de bits no operen en parells de bits corresponents, i per tant no poden ser anomenats pròpiament com "bit a bit" (bit d'adreça). En aquestes operacions els dígits (bits) són moguts, o desplaçats, cap a l'esquerra o cap a la dreta. Els registres en un processador d'ordinador tenen una amplada fixa, així que alguns bits "seran desplaçats cap a fora" ("shifted out"), és a dir, "surten" del registre per un extrem, mentre que el mateix nombre de bits són "desplaçats cap a dintre" ("shifted in"), és a dir, "entren" per l'altre extrem, les diferències entre els operadors de desplaçament de bits estan en com aquests determinen els valors dels bits que entren al registre (desplaçament cap a dins) (shifted-in).

Desplaçament lògic

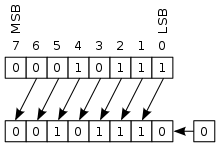
Hi ha dos desplaçaments lògics (logical shifts). El desplaçament lògic cap a l'esquerra (left shift) i el desplaçament lògic cap a la dreta (right shift). En el desplaçament lògic els bits d'un registre són desplaçats (moguts) una o més posicions cap a la dreta o cap a l'esquerra. Els bit que surten del registre per un extrem es perden i en l'altre extrem del registre s'omple amb un bit zero per cada bit desplaçat. Aquesta operació s'efectua mitjançant registres de desplaçament.

Per exemple. Si es té en un registre de 8 bits el valor 10110011, i es fa un desplaçament cap a l'esquerra d'un bit, tots els bits es mouen una posició cap a l'esquerra, el bit de l'esquerra es perd i entra un bit zero de farciment pel costat dret. En un desplaçament d'un bit cap a la dreta passa alguna cosa semblant, el bit de la dreta es perd i el de l'esquerra s'omple amb un zero:

10110011 10110011 <-- Bits abans del desplaçament
1 <-- 0110011 <-- 0 0 --> 1011001 --> 1 <-- Desplaçament
01100110 01011001 <-- Bits després del desplaçament
desplaçament desplaçament
 cap a l'esquerra cap a la dreta

En determinats processadors, queda emmagatzemat l'últim bit que va sortir amb el desplaçament del registre. En la sèrie dels processadors x86 aquest bit queda emmagatzemat en el flag del ròssec.

Movent bits

El desplaçament lògic s'usa per moure bits cap a l'esquerra o cap a la dreta per col·locar en la posició adequada.

Per exemple, suposem que tenim, en dos registres de la mida d'un byte, a dos dígits hexadecimals (en representació binària de 4 bits cada un), i es vol empaquetar en un sol byte, on els 4 bits superiors és l'hexadecimal més significatiu i els 4 bits inferiors és l'hexadecimal menys significatiu:

0000 1001 <-- Dígit hexadecimal més significatiu (hexadecimal 9)
0000 1010 <-- Dígit hexadecimal menys significatiu (hexadecimal A)

Per empaquetar en un sol byte, primer cal desplaçar l'hexadecimal més significatiu 4 posicions cap a l'esquerra. (Això es fa amb el desplaçament lògic cap a l'esquerra):

1001 0000 <-- hexadecimal 9, desplaçat 4 bits cap a l'esquerra per posar-lo a la posició correcta dins del byte

Després, es fa un OR dels dos valors que contenen els dígits hexadecimals perquè quedin combinats en un sol byte:

0000 1010 <-- Hexadecimal menys significatiu A
OR 1001 0000 <-- OR amb l'hexadecimal més significatiu 9, el qual ja està en la seva posició
1001 1010 <-- Byte amb els dos hexadecimals empaquetats (hexadecimal 9A)

Ara tenim un byte amb el valor de 1001 1010, el qual té els dos dígits hexadecimals empaquetats.

Multiplicació i divisió per 2ⁿ, d'enters sense signe

En nombres enters sense signe, el desplaçament lògic cap a l'esquerra equival a una multiplicació per 2 i el desplaçament lògic cap a la dreta equival a una divisió per 2. A la divisió (desplaçament cap a la dreta), es perd el bit menys significatiu, donant com a resultat un truncament del resultat (arrodoniment cap avall, cap a menys infinit). Així, 6/2 és igual a 3, però 7/2 és igual a 3,5, però el 0,5 es perd quedant el resultat en 3.

Els programadors de llenguatge assemblador usen aquesta propietat per fer multiplicacions i divisions ràpides, d'enters sense signe, per una potència de 2, on n desplaçaments equivalen a multiplicar o dividir per 2ⁿ. També, si el processador no té operacions de multiplicació i divisió d'enters, o si aquestes són molt lentes, es pot multiplicar o dividir usant desplaçaments i sumes per multiplicar i desplaçaments i restes per dividir. Per exemple, per multiplicar un enter per 10, es procedeix de la manera següent (en el llenguatge assemblador del x86):

Es vol multiplicar el contingut del registre EAX per 10:

En les instruccions de sota, EAX i EBX són registres del processador, SHL (shift left), desplaça el registre indicat una posició (un bit) cap a l'esquerra (que equival a multiplicar per 2), MOV copia el registre de la dreta sobre el registre de l'esquerra, i ADD afegeix el registre de la dreta al registre de l'esquerra.

SHL EAX, 1; EAX = EAX * 2 EAX = 2n, desplaça a l'esquerra el contingut del registre EAX una posició,
                                               ; (Multiplica EAX per 2)
MOV EBX, EAX; EBX = EAX EBX = 2n, còpia el registre EAX en EBX, ara els dos registres tenen 2n
SHL EBX, 1; EBX = EBX * 2 EBX = 4n; multiplica EBX per 2, obtenint 4n
SHL EBX, 1; EBX = EBX * 2 EBX = 8n; torna a multiplicar EBX per 2, obtenint 8n
ADD EAX, EBX; EAX = EAX + EBX EAX = 2n + 8n = 10n; suma EBX (8n) a EAX (2n),
                                                         ; (Ara EAX té el valor original multiplicat per 10)

Desplaçament aritmètic

Els desplaçaments aritmètics són similars als desplaçaments lògics, només que els aritmètics estan pensats per treballar sobre nombres enters amb signe en representació de complement a dos en lloc d'enters sense signe. Els desplaçaments aritmètics permeten la multiplicació i la divisió per dos, de nombres enters amb signe, per una potència de dos. Desplaçar n bits cap a l'esquerra o a la dreta equival a multiplicar o dividir per 2 ⁿ, (assumint que el valor no fa desbordament (overflow o underflow)).

El desplaçament aritmètic a l'esquerra és exactament igual al desplaçament lògic cap a l'esquerra. De fet són dos noms diferents per exactament la mateixa operació. En desplaçar els bits una posició cap a l'esquerra és equivalent a una multiplicació per 2 independentment de si és un nombre enter amb signe o sense signe. En els processadors x86, el assemblador té dos pnemònics per al desplaçament lògic i l'aritmètic cap a l'esquerra, però quan el programa és ensamblat, només hi ha un opcode per tots dos a les instrucció en llenguatge de màquina.

El desplaçament aritmètic cap a la dreta és diferent al desplaçament lògic cap a la dreta. En els sencers sense signe, per dividir per 2, s'ha d'usar el desplaçament lògic, el qual sempre afegeix un 0 a l'extrem esquerre per cada desplaçament d'un bit a la dreta. En canvi, en els enters amb signe, s'ha d'usar el desplaçament aritmètic cap a la dreta, el qual copia el bit del signe (el bit més significatiu (MSB)) en l'espai buit que queda a l'extrem esquerre cada vegada que es fa un desplaçament d'un bit a la dreta. D'aquesta manera, es divideix efectivament per 2 a l'enter amb signe.

Si el sencer amb signe és positiu, (amb el bit del signe igual a 0), s'inserirà el bit 0 del signe a l'extrem esquerre en desplaçar un bit cap a la dreta (com el desplaçament lògic cap a la dreta), però si és un enter negatiu, (amb el bit del signe igual a 1), s'inserirà el bit 1 del bit del signe a l'extrem esquerre. D'aquesta manera, el signe del nombre es preserva amb la divisió per 2 i el nombre resultant té sentit. Si es inserir un 0 a l'esquerra a un nombre negatiu (com ho faria el desplaçament lògic cap a la dreta), en primer lloc, aquest nombre negatiu canviaria de signe a positiu, i en segon lloc, la interpretació dels bits restants no tindrien sentit.

Aquests exemples utilitzen un registre de 8 bits:

00010111 (Decimal 23) (Desplaçament aritmètic cap a l'esquerra d'un nombre positiu)
= 00101110 (Decimal 46) (El bit de l'esquerra es perd i un bit 0 s'afegeix a la dreta)

11010111 (Decimal -41) (Desplaçament aritmètic cap a l'esquerra d'un nombre negatiu)
= 10101110 (Decimal -82) (El bit de l'esquerra es perd i un bit 0 s'afegeix a la dreta)

00010111 (Decimal 23) (Desplaçament aritmètic cap a la dreta d'un nombre positiu)
= 00001011 (Decimal 11) (El bit de la dreta es perd i el bit del signe anterior conserva en el resultat)

11010111 (Decimal -41) (Desplaçament aritmètic cap a la dreta d'un nombre negatiu)
= 11101011 (Decimal -21) (El bit de la dreta es perd i el bit del signe anterior es conserva en el resultat)

Si el nombre binari és tractat com complement a u, llavors la mateixa operació de desplaçament cap a la dreta és en una divisió per 2 ⁿ arrodonint cap al zero.

Operacions de Rotació

Rotació

Una altra forma de desplaçament és el desplaçament circular o rotació de bits. En aquesta operació, els bits d'un registre són "rotats" d'una manera circular com si els extrems esquerre i dret del registre estiguessin connectats. En la rotació cap a l'esquerra, el bit que surt per l'extrem esquerre entrarà per l'extrem dret, i viceversa amb la rotació cap a la dreta. Aquesta operació és útil si és necessari conservar tots els bits existents, i és freqüentment usada en criptografia digital.

Rotació mitjançant el bit de ròssec

Rotar a través del bit de l'implico és similar a l'operació de girar anterior (rotació sense implico). La diferència està en el fet que els dos extrems del registre estan units entre si a través del flag de ròssec, el qual queda enmig d'ells. El bit que surt per un extrem va al flag del implico, i el bit original que estava en el flag de l'implico entra al registre per l'extrem oposat.

Si es fixa el flag del implico per endavant, una rotació simple a través del implico pot simular un desplaçament lògic o aritmètic d'una posició. Per exemple, si el flag del implico conté 0, després d'una rotació cap a la dreta a través del flag de l'implico, equival a un desplaçament lògic cap a la dreta, i si el flag del ròssec conté una còpia del bit del signe, equival a un desplaçament aritmètic cap a la dreta. Per això, alguns microcontroladors com ara els PIC només tenen les funcions de girar i girar a través de l'implico, i no es preocupen de tenir instruccions de desplaçament aritmètic o lògic.

Rotar a través del implico és especialment útil quan es fan desplaçaments en nombres més grans que la mida natiu de la paraula del processador, perquè si, per ara, un nombre gran és emmagatzemat en dos registres i es vol desplaçar cap a la dreta un bit, el bit que surt de l'extrem dret del registre de l'esquerra ha d'entrar per l'extrem esquerre del registre de la dreta. Amb rotació a través del implico, aquest bit és "emmagatzemat" al flag de l'implico durant el primer desplaçament cap a la dreta sobre el registre de l'esquerra, a punt per ser desplaçat al registre de la dreta usant una simple rotació amb implico cap a la dreta i sense utilitzar cap preparació extra.

Vegeu també