Operador tensor

En matemàtiques pures i aplicades, mecànica quàntica i gràfics per ordinador, un operador tensor generalitza la noció d' operadors que són escalars i vectors. Una classe especial d'aquests són els operadors de tensors esfèrics que apliquen la noció de la base esfèrica i els harmònics esfèrics. La base esfèrica està estretament relacionada amb la descripció del moment angular en mecànica quàntica i funcions harmòniques esfèriques. La generalització lliure de coordenades d'un operador tensor es coneix com a operador de representació.^[1]

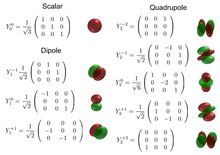
La noció general d'operadors escalar, vectorial i tensor

En mecànica quàntica, els observables físics que són escalars, vectors i tensors s'han de representar mitjançant operadors escalar, vectorial i tensor, respectivament. Que una cosa sigui un escalar, un vector o un tensor depèn de com ho veuen dos observadors els marcs de coordenades dels quals estan relacionats entre si mitjançant una rotació. Alternativament, es pot preguntar com, per a un únic observador, una magnitud física es transforma si es gira l'estat del sistema. Considerem, per exemple, un sistema format per una molècula de massa $M$ , viatjant amb un centre de masses definit, $p{\mathbf {\hat {z}} }$ , a la $z$ direcció. Si fem girar el sistema $90^{\circ }$ sobre l'eix $y$ , l'impuls canviarà a $p{\mathbf {\hat {x}} }$ , que es troba a la $x$ direcció. Tanmateix, l'energia cinètica del centre de massa de la molècula es mantindrà inalterada $p^{2}/2M$ . L'energia cinètica és un escalar i el moment és un vector, i aquestes dues magnituds s'han de representar per un escalar i un operador vectorial, respectivament. Amb aquest últim en particular, ens referim a un operador els valors esperats del qual en els estats inicial i girat són $p{\mathbf {\hat {z}} }$ i $p{\mathbf {\hat {x}} }$ . L'energia cinètica, en canvi, s'ha de representar mitjançant un operador escalar, el valor esperat del qual ha de ser el mateix en els estats inicial i girat.^[2]

De la mateixa manera, les magnituds tensorials s'han de representar mitjançant operadors tensorials. Un exemple de magnitud tensor (de rang dos) és el moment quadripolar elèctric de la molècula anterior. Així mateix, els moments octupol i hexadecapol serien tensors de rang tres i quatre, respectivament.

Altres exemples d'operadors escalars són l'operador d'energia total (més comunament anomenat Hamiltonià), l'energia potencial i l'energia d'interacció dipol-dipol de dos àtoms. Exemples d'operadors vectorials són el moment, la posició, el moment angular orbital, ${\mathbf {L} }$ , i el moment angular de spin, ${\mathbf {S} }$ . (Letra petita: el moment angular és un vector pel que fa a les rotacions, però a diferència de la posició o el moment, no canvia de signe sota inversió espacial, i quan es vol proporcionar aquesta informació, es diu que és un pseudovector).

Els operadors escalars, vectorials i tensorials també es poden formar per productes d'operadors. Per exemple, el producte escalar ${\mathbf {L} }\cdot {\mathbf {S} }$ dels dos operadors vectorials, ${\mathbf {L} }$ i ${\mathbf {S} }$ , és un operador escalar, que ocupa un lloc destacat en les discussions sobre la interacció espín-òrbita. De la mateixa manera, el tensor de moment quadripolar de la nostra molècula d'exemple té els nou components

$Q_{ij}=\sum _{\alpha }q_{\alpha }\left(3r_{\alpha ,i}r_{\alpha ,j}-r_{\alpha }^{2}\delta _{ij}\right).$ Aquí, els índexs $i$ i $j$ pot prendre independentment els valors 1, 2 i 3 (o $x$ , $y$ , i $z$ ) corresponent als tres eixos cartesians, l'índex $\alpha$ recorre totes les partícules (electrons i nuclis) de la molècula, $q_{\alpha }$ és la càrrega de la partícula $\alpha$ , i $r_{\alpha ,i}$ és el $i$ -è component de la posició d'aquesta partícula. Cada terme de la suma és un operador tensor. En particular, els nou productes $r_{\alpha ,i}r_{\alpha ,j}$ junts formen un tensor de segon rang, format prenent el producte exterior de l'operador vectorial ${\mathbf {r} }_{\alpha }$ amb si mateix.^[3]