Oscil·lació amortida
Una oscil·lació amortida, o esmorteïda, és un tipus d'oscil·lació, no aïllada, en què l'amplitud de l'oscil·lació decreix exponencialment amb el temps. A diferència de l'harmònica, que oscil·laria de forma indefinida, acaba aturant-se a causa de l'amortiment. És un fenomen comú que es pot observar a moltes situacions del món real, pèndols, molles… Aquest descens de l'amplitud i l'energia de l'oscil·lació, que es converteix en energia tèrmica, sol ser causada pel fregament del cos oscil·lant amb el medi d'oscil·lació o per les mateixes característiques de la força impulsora.

La forma més simple d'expressar aquests factors que fan disminuir l'energia mecànica del cos és mitjançant la introducció d'una força de fregament proporcional a la velocitat de desplaçament, , que a nivell teòric representa totes les forces que fan aturar el cos. Aquesta força, com es pot comprovar, s'oposa al moviment, és negativa, i depèn de b, una constant positiva anomenada constant de proporcionalitat o coeficient de fricció.
Equació de moviment
[modifica]Per deduir l'equació del moviment, en cas que la partícula oscil·li diverses vegades, es parteix de la segona llei de Newton, la llei fonamental de la dinàmica:
Aleshores, si ens imaginem una molla simple lligada a una massa que oscil·la horitzontalment podem imaginar-nos que les forces que actuen sobre el cos són la força recuperadora (que sempre és negativa) i la força d'amortiment (originada pel contacte amb el terra i l'aire, i que s'oposa al moviment, sent també negativa). I, substituint per les variables, ens queda:
D'on, passant les forces a l'altra banda de l'equació i dividint-la tota per m, es pot extreure que l'equació del moviment és:
Que també es pot escriure amb els següents termes:
on és la freqüència natural d'oscil·lació (la freqüència amb la qual oscil·laria el sistema si fos una oscil·lació harmònica aïllada sense fregament) i la beta és la constant d'amortiment.
I si se n'extreu la solució queda l'expressió simple que quantifica l'amplitud següent:
On és la freqüència real d'oscil·lació, que es pot quantificar amb la fórmula: .
Els elements cosinus de l'equació es poden simplificar a 1 en segons quins exercicis, com els de pèrdua d'energia o amplitud, ja que així només es considera el punt de màxima amplitud. I si ens fixem en aquesta equació simplificada veiem clarament que l'amplitud decreix exponencialment a mesura que passa el temps.
Aquesta equació és vàlida pel tipus d'oscil·lació anomenada subamortida, que s'explica a continuació.
Tipus d'oscil·lació amortida
[modifica]Hi ha tres tipus d'oscil·lació amortida segons la seva evolució temporal:
- Sobreamortida, en aquest cas el sistema no pot oscil·lar i retorna lentament al punt d'equilibri.
- Amortida críticament, la freqüència d'oscil·lació és zero i torna gradualment a la posició d'equilibri. Aquest tipus d'esmorteïment és especialment útil per a sistemes on es volen reduir les oscil·lacions perquè retorna
- Subamortida, l'amplitud de les oscil·lacions va disminuint de mica en mica.
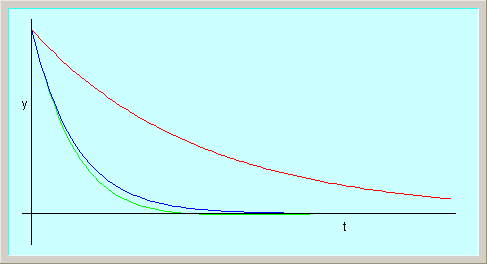
| Corba blava: amortiment crític. |
| Corba vermella: moviment sobreamortit, el doble del crític. |
| Corba verda: moviment subamortit, d'amortiment igual a 90% de l'amortiment crític. |
Oscil·lació sobreamortida
[modifica]És el fenomen que s'esdevé quan l'amortiment és molt alt (per exemple, un pèndol que oscil·la en melassa). En aquest cas, l'oscil·lador no pot completar ni una sola oscil·lació i es mou cap a la posició d'equilibri amb una velocitat baixa, respecte als altres tipus, que tendeix a zero quan s'acosta al punt d'equilibri.
Oscil·lació amortida críticament
[modifica]En aquest cas el sistema retorna a la seva posició d'equilibri el màxim de ràpid possible. En aquesta situació l'amortiment és el mínim necessari per evitar que es creï el moviment oscil·latori.
Oscil·lació subamortida
[modifica]També anomenada oscil·lació amortida simplement, és el moviment que s'esdevé quan l'amortiment que s'aplica al cos és feble i l'amplitud i l'energia decreixen lentament en el temps. Aquest tipus de moviment, a diferència dels anteriors, sí que realitza més d'una oscil·lació completa.
Pot arribar a ser molt i molt semblant a un moviment harmònic simple, si el seu amortiment és feble. Aquest cas es coneix com a les oscil·lacions poc amortides on .
On:
- és la massa de l'oscil·lador.
- és la freqüència angular real.
- és la freqüència angular que tindria si fos un MHS.
Energia de l'oscil·lació poc amortida
[modifica]L'energia mecànica total a un moviment oscil·latori esmorteït no es manté constant. En els casos sobreamortit i amortit críticament l'energia del moviment es dissipa ràpidament perquè no hi ha oscil·lació, en canvi en el cas de l'oscil·lació subamortida oscil·la i va perdent aquesta energia de mica en mica a cada cicle. L'energia mecànica total serà igual a la potència consumida per la força de fricció, matemàticament:
Aquesta potència és negativa perquè perd l'energia en forma de calor. Considerant que la pèrdua d'energia a cada cicle és petita es pot substituir pel seu valor mitjà:
Que indica un decreixement exponencial, com en el cas de l'amplitud, de l'energia del sistema. Així:
on C és una constant d'integració. Aleshores, aplicant l'exponencial a les dues bandes de l'equació obtenim:
On és la constant d'energia a l'instant inicial. D'aquesta equació en podem concloure que l'energia d'un moviment oscil·latori amortit disminueix el doble de ràpid que l'amplitud en aquest mateix moviment.
El temps de relaxació
[modifica]De vegades per determinar les pèrdues d'energia es fa servir un concepte anomenat temps de relaxació simbolitzat amb el caràcter grec (). Aquest terme quantifica el temps que tarda l'amplitud o l'energia a reduir-se a un 37% de la inicial. Així doncs, matemàticament es pot expressar l'energia també en funció d'aquest terme:
I en el cas de l'energia, com que disminueix el doble de ràpid que l'amplitud és:
On és el temps de relaxació de l'amplitud, és el temps de relaxació de l'energia i l'última fórmula és l'energia expressada amb el temps de relaxació.
El factor de qualitat
[modifica]Normalment per determinar la pèrdua d'energia d'un oscil·lador s'usa el factor de qualitat Q, definit per:
On és l'energia perduda en un cicle.
Finalment, amb el factor de qualitat es pot relacionar la freqüència natural amb la real mitjançant la fórmula:
Aplicacions
[modifica]El coneixement de les oscil·lacions amortides és important per al disseny i construcció de molts components de l'enginyeria moderna. Per exemple els amortidors dels cotxes, el tren d'aterratge dels avions, suports per a màquines a la indústria... També serveix a enginyeria estructural per a millorar les estructures contra perills com terratrèmols o altres moviments que poden patir les estructures.
Suspensió de vehicles
[modifica]A un vehicle serveix per calcular com han de ser els amortidors. Un amortidor òptim per a un vehicle és el que segueix la corba d'amortiment crítica, perquè retorna a l'estabilitat al més ràpidament possible fent així que el vehicle s'estabilitzi ràpidament. Això millora la comoditat i la seguretat al conduir gràcies a la reducció de les pertorbacions. Sense amortidors el vehicle trontollaria a cada desnivell.

Ferrocarrils
[modifica]Els trens incorporen un amortidor transversal, anomenat amortidor de guinyada, que ajuda a evitar que els vagons es belluguin de banda a banda. Són presents a la majoria de trens, ja siguin de mercaderies o de passatgers, i també són útils perquè són un element que ajuda a evitar descarrilaments.
Referències
[modifica]- Tipler, Paul A. Física per a la ciència i la tecnologia. Vol.1. Editorial Reverté, 2011. ISBN 9788429144321.
- «Teoria d'Oscil·lacions». Universitat Pompeu Fabra. Arxivat de l'original el 2016-03-03. [Consulta: 19 gener 2013].
- Serway, R.A.. Física, Volúmenes 1 y 2, 3ª edición. Editorial Thomson Paranimfo, 2003.





























