Paraboloide
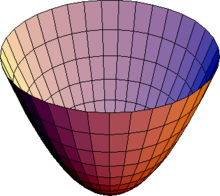

Un paraboloide és la superfície quàdrica tal que en cada un dels seus punts de la superfície hi podem fer passar un pla de manera que la secció de la superfície per aquest pla sigui una paràbola.[1] De vegades el terme paraboloide es fa servir per referir-se específicament al paraboloide de revolució.
Segons les seccions que es poden obtenir en altres direccions tenim diferents tipus de paraboloide.
Un paraboloide de revolució[2] és la superfície il·limitada formada pels punts que equidisten d'un punt fix anomenat focus i un pla anomenat director.
Aquesta és l'equació del paraboloide de distància p del focus al pla director, amb el pla director perpendicular a l'eix x i el focus a l'origen de coordenades:
y² + z² = 2 · p · x
Es pot entendre com format per la revolució d'una paràbola al voltant del seu eix.[2] És un cas particular del paraboloide el·líptic on les el·lipses tenen iguals els dos eixos i són cercles (paraboloide circular).
Referències
[modifica]- ↑ «paraboloide». Gran Enciclopèdia Catalana.
- ↑ 2,0 2,1 «paraboloide de revolució». Gran Enciclopèdia Catalana.
