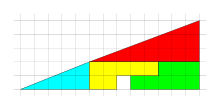
Paradoxa del quadrat perdut

Animació de la paradoxa del quadrat perdut

La paradoxa del quadrat perdut o trencaclosques del quadrat perdut és una il·lusió òptica utilitzada en matemàtiques per a raonar sobre les figures geomètriques. La paradoxa té en compte un triangle compost de quatre peces, com en un trencaclosques. En la paradoxa es presenten dos triangles formats per les mateixes peces però distribuïdes de manera diferent. En els dos casos els triangles presenten les mateixes dimensions, 13 de base i 5 d'alçada, però en un dels casos hi ha un quadrat buit. D'acord amb Martin Gardner, aquest trencaclosques va ser inventat per un mag de la ciutat de Nova York, Paul Curry, l'any 1953. Tot i això, els principis de les paradoxes de dissecció es coneixen des del segle xvi.

Les peces

Les quatre peces que constitueixen el trencaclosques tenen una forma i superfície concreta i invariable. L'àrea de cada peça és:

La peça vermella

La peça vermella és un triangle rectangle de base 8 i alçada 3, i per tant la seva àrea serà:

$A_{ro}={\cfrac {8\cdot 3}{2}}=12$

La peça blava

La peça blava també és un triangle rectangle, però, en aquest cas presenta una base 5 i una alçada 2, i per tant la seva àrea serà:

$A_{az}={\cfrac {5\cdot 2}{2}}=5$

La peça verda

La peça verda és un rectangle de base 5 i alçada 2 al qual li manca un rectangle de dimensions 2x1; l'àrea de la peça verda és:

$A_{ve}=5\cdot 2-2\cdot 1=8$

La peça groga

La peça groga és un rectangle de base 5 i alçada 2 al qual li manca un rectangle de dimensions 3x1; l'àrea de la peça groga és:

$A_{am}=5\cdot 2-3\cdot 1=7$

La paradoxa

Les quatre peces (groga, vermella, verda i blava) ocupen una superfície de:

${\begin{array}{lcr}A_{ro}&=&12\\A_{az}&=&5\\A_{ve}&=&8\\A_{am}&=&7\\\hline total&=&32\end{array}}$

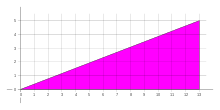
però el triangle té unes dimensions de 13 de base i 5 d'alçada, per tant la seva àrea serà:

$A_{T}={\cfrac {13\cdot 5}{2}}=32,5$

La solució de la paradoxa és simple: la figura presentada com un triangle no ho és en realitat, ja que presenta quatre costats i no tres com qualsevol triangle; la seva suposada hipotenusa no és completament recta, sinó que presenta dos pendents lleugerament diferents.

Passa pels punts sense alinear (0,0) (8,3) i (13,5).	Passa pels punts sense alinear (0,0) (5,2) i (13,5).
La superfície és de 32 quadrats.	La superfície és de 32 quadrats.

Si comparem els angles d'inclinació de la hipotenusa respecte a la base dels triangles vermells i blaus veuren que difereixen. L'angle del triangle vermell és:

$\tan(\alpha _{ro})={\frac {3}{8}}\;\longrightarrow \quad \alpha _{ro}=20^{\circ }33^{\prime }21.76^{\prime \prime }$

mentre que en el blau és:

$\tan(\alpha _{az})={\frac {2}{5}}\;\longrightarrow \quad \alpha _{az}=21^{\circ }48^{\prime }5.05^{\prime \prime }$

i en el triangle total és:

$\tan(\alpha _{T})={\frac {5}{13}}\;\longrightarrow \quad \alpha _{T}=21^{\circ }2^{\prime }15.04^{\prime \prime }$

Els punts (0,0), (5,2), (8,3) i (13,5) no es troben alineats, tot i que la diferència és petita, les dues figures representades en la paradoxa són quadrilàters i no triangles; l'angle en (5,2) és còncau mentre que el de (8,3) és convex. I la diferència entre les dues figures és el quadrat que suposadament apareix a la part superior.

Si des del punt (0,0) tracem els tres angles prolongant les rectes, la diferència geomètrica és molt evident.

La solució

Aquesta diferència pot semblar petita per l'espessor, però degut a la seva longitud la seva superfície és igual al quadrat unitari que manca en la paradoxa.

Enllaços externs

• Versió imprimible de la paradoxa del quadrat perdut amb un vídeo de demostració.
• Curry's Paradox: How Is It Possible?
• Triangles and Paradoxes
• Paradoxa aplicada a una rajola de xocolata Arxivat 2016-03-04 a Wayback Machine..
• The Triangle Problem or What's Wrong with the Obvious Truth Arxivat 2007-06-21 a Wayback Machine.