Vés al contingut

Parell de Tussí

De la Viquipèdia, l'enciclopèdia lliure
(S'ha redirigit des de: Parell de Tusi)
Model animat del parell de Tussí.

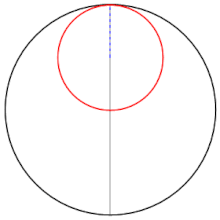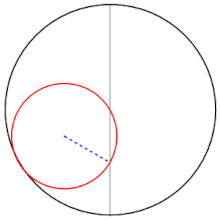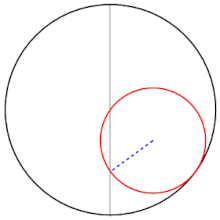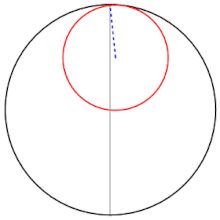
El parell de Tussí és una construcció geomètrica dissenyada per l'astrònom persa Nassir-ad-Din at-Tussí (1201-1274) que consisteix en la substitució dels epicicles de Claudi Ptolemeu per un petit cercle que gira dins la circumferència d'un altre cercle de radi doble.[1] La rotació dels dos cercles origina un punt en la circumferència del cercle petit que oscil·la avant i enrere i causa un moviment lineal sobre el diàmetre del cercle gran.

Definició

[modifica]

Al parell de Tusí se'l descriu de vegades com un petit cercle que rutlla per l'interior d'un altre cercle més gran que està fixe. L'astrònom Tussí el descrivia, però, de forma diferent:

«Si dos cercles en un mateix pla, el diàmetre d'un dels quals és igual a la meitat del de l'altre, se situen de manera que siguin internament tangents a un punt, i si un punt agafat del cercle menor que coincideixi amb el punt de tangència, i si els dos cercles es mouen en moviment simple però en sentits oposats de manera que el moviment del menor sigui el doble que el del gran, per tant el petit completarà dues rotacions per cada rotació del gran, llavors aquell punt serà vist en moviment sobre el diàmetre del cercle més gran que inicialment passava pel punt tangencial, oscil·lant entre dos extrems.»

—[2]

Creació

[modifica]
dibuixos del moviment del parell de Tussí, en una còpia del segle xiv del manuscrit original.[3]

Aquesta construcció geomètrica va ser proposada per primera vegada per un astrònom i matemàtic del segle xiii anomenat Nassir-ad-Din at-Tussí, el qual va escriure el 1247 una obra titulada Tahrir al-Majisti (‘Comentari a Almagest’) on va incloure aquesta idea com a solució al moviment latitudinal dels planetes inferiors,[4] i més endavant la va aplicar com a substitució de l'equant, un concepte presentat uns mil anys abans en l'Almagest de Claudi Ptolemeu.[5][6]

Nassir-ad-Din at-Tussí, nascut a la ciutat de Tus el 1201, és conegut en la cultura islàmica com un dels grans savis. Tussí va ser el primer astrònom que va cercar una solució per definir el moviment latitudinal dels astres sense fer servir un component longitudinal. Per fer això va proposar en un treball anomenat Tahrlr al-Majisti, que va acabar el 1247, que el moviment oscil·latori està produït pels moviments circulars uniformes combinats de dos cercles idèntics, un voltant dins la circumferència de l'altre. Tussí simplement estableix que si un d'aquests cercles s'hagués de moure a una velocitat uniforme igual al de l'altre i en una direcció cap a ell, llavors qualsevol punt de la circumferència del primer cercle oscil·larà en línia recta sobre un dels diàmetres del segon cercle.[7]

Llibres en què és descrit

[modifica]

L'expressió "parell de Tussí" és de creació moderna, proposada per Edward Kennedy el 1966.[8] És una de diverses construccions astronòmiques de la cultura islàmica que té una sorprenent semblança amb el model emprat per Nicolau Copèrnic en De revolutionibus, aplicat al planeta Mercuri i a la seva teoria de la trepidació. Els historiadors sospiten que Copèrnic o algun altre autor europeu va tenir accés al text de Tussí, i com a possibles transmissors s'han suggerit: Guillaume Postel un home del segle xvi que coneixia l'àrab i el grec i va viatjar a Constantinoble,[9][10] o Gregori Coniades que va viatjar a Pèrsia al segle xiii per aprendre astronomia, va conèixer en persona a Tussí, i en va fer diverses traduccions al grec.[11]

Atès que el parell de Tussí fou emprat per Copèrnic en l'explicació matemàtica de la seva teoria astronòmica, hi ha un creixent consens que ell tenia coneixement d'aquesta idea, ja formulada anteriorment. S'ha suggerit[12] que la idea del parell de Tussí podria haver arribat a Europa a través d'uns pocs manuscrits sense que hi hagués cap traducció directa de l'àrab al llatí. Una possible ruta de transmissió podria ser a través de Trebisonda on hi havia una escola d'astronomia. Alguns manuscrits d'astronomia escrits en grec medieval, en els quals es descriu el parell de Tussí, es conserven a Itàlia.[13]

Hi ha altres obres en les quals s'ha aplicat aquest model per explicar el moviment circular en relació al moviment lineal recíproc. Es pot trobar en el Commentari al primer llibre d'Euclides, escrit per Procle[14] i el concepte era conegut a París a mitjan segle xiv. El francès Nicolau Oresme, en la seva obra Qüestions sobre l'esfera (escrita abans del 1362), va descriure com combinar el moviment circular per tal de produir un moviment lineal recíproc d'un planeta dins el radi del seu epicicle. La descripció que en va fer Oresme no és gaire clara i no està clar si la idea va ser pròpia o si va ser el resultat de traduir amb poca manya un text àrab.[15]

Hipotrocoide

[modifica]
Article principal: Hipotrocoide

Una propietat del parell de Tusi és que assenyala que el punt del cercle interior que no es troba a la circumferència de traça el·lipses). Aquests el·lipses i la recta traçada pel clàssic parell de Tusi són casos especials d'hipotrocoides.[16]

Referències

[modifica]
  1. ↑ Gingerich, Owen «Islamic Astronomy» (en anglès). Scientific American, 254, 4, 1986, pàg. 74–83. Bibcode: 1986SciAm.254d..74G. DOI: 10.1038/scientificamerican0486-74. JSTOR: 24975932.
  2. ↑ Ragep, 1993, p. 194-196.
  3. ↑ Biblioteca Vaticana, arxiu vaticà 319 foli 28 verso math19 NS.15
  4. ↑ Saliba, 1995, p. 152-155.
  5. ↑ Kennedy, 1966, p. 365-378.
  6. ↑ Fraser, 2006, p. 39.
  7. ↑ Saliba i Kennedy, 2007, p. 285-291.
  8. ↑ Kennedy, 1966, p. 370.
  9. ↑ Saliba, 1996, p. 709-718.
  10. ↑ George Saliba, Whose Science is Arabic Science in Renaissance Europe?, Columbia University
  11. ↑ Pingree, 1964, p. 135-160.
  12. ↑ Kren, 1971, p. 497.
  13. ↑ George Saliba, Islamic Science and Europe, The Library of Congress
  14. ↑ Veselovsky, 1973, p. 128-130.
  15. ↑ Kren, 1971, p. 490-492.
  16. ↑ Brande, p. 1875.

Bibliografia

[modifica]
  • Brande, W.T.. A Dictionary of Science, Literature, & Art (en anglès). Longmans, Green, and Company, 1875. 
  • Di Bono, Mario «Copernicus, Amico, Fracastoro and Tusi's Device: Observations on the Use and Transmission of a Model». Journal for the History of Astronomy, 26, 1995, pàg. 133-154.
  • Fraser, Craig G. The cosmos: a historical perspective. Greenwood Publishing Group, 2006. 
  • Kennedy, E. S. «Late Medieval Planetary Theory». Isis, 57, 3, 1966.
  • Kren, Claudia «The Rolling Device of Naṣir al-Dīn al-Ṭūsī in the De spera of Nicole Oresme». Isis, 62, 1971.
  • Pingree, David «Gregory Chioniades and Palaeologan Astronomy». Dumbarton Oaks Papers, 18, 1964.
  • Ragep, F. J.. Nasir al-Din al-Tusi's "Memoir on Astronomy", Sources in the History of Mathematics and Physical Sciences. 12. 2. Nova York: Springer, 1993. ISBN 3-540-94051-0. 
  • Ragep, F. J.. «The Two Versions of the Tusi Couple». A: From Deferent to Equant: A Volume of Studies in the History of Science in Ancient and Medieval Near East in Honor of E. S. Kennedy (Annals of the New York Academy of Sciences, 500). New York Academy of Sciences, 1987. ISBN 0-89766-396-9. 
  • Saliba, George. A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam, 1995. 
  • Saliba, George «Writing the History of Arabic Astronomy: Problems and Differing Perspectives». Journal of the American Oriental Society, 116, 4, 1996.
  • Saliba, George; Kennedy, E. S.. Arabic Sciences and Philosophy. Springer, 2007. 
  • Veselovsky, I. N. «Copernicus and Nasir al-Din al-Tusi». Journal for the History of Astronomy, 4, 1973.
A Wikimedia Commons hi ha contingut multimèdia relatiu a: Parell de Tussí
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Parell_de_Tussí&oldid=33024661»