Problema de dos cossos en relativitat general

El problema de dos cossos en la relativitat general (o problema relativista de dos cossos) és la determinació del moviment i el camp gravitatori de dos cossos tal com es descriu per les equacions de camp de la relativitat general. Resoldre el problema de Kepler és essencial per calcular la flexió de la llum per gravetat i el moviment d'un planeta que orbita el seu sol. Les solucions també s'utilitzen per descriure el moviment de les estrelles binàries unes al voltant de les altres i estimar la seva pèrdua gradual d'energia a través de la radiació gravitatòria.

La relativitat general descriu el camp gravitatori mitjançant l'espai-temps corbat; les equacions de camp que regeixen aquesta curvatura són no lineals i per tant difícils de resoldre en forma tancada. No s'han trobat solucions exactes del problema de Kepler, però sí una solució aproximada: la solució de Schwarzschild. Aquesta solució correspon quan la massa M d'un cos és aclaparadorament més gran que la massa m de l'altre. Si és així, la massa més gran es pot considerar estacionària i l'únic que contribueix al camp gravitatori. Aquesta és una bona aproximació per a un fotó que passa per una estrella i per a un planeta que orbita el seu sol. El moviment del cos més lleuger (anomenat "partícula" a continuació) es pot determinar a partir de la solució de Schwarzschild; el moviment és un geodèsic ("camí més curt entre dos punts") en l'espai-temps corbat. Aquestes solucions geodèsiques expliquen la precessió anòmala del planeta Mercuri, que és una evidència clau que recolza la teoria de la relativitat general. També descriuen la flexió de la llum en un camp gravitatori, una altra predicció famosa com a prova de la relativitat general.

Si es considera que ambdues masses contribueixen al camp gravitatori, com en les estrelles binàries, el problema de Kepler només es pot resoldre aproximadament. El primer mètode d'aproximació que es va desenvolupar va ser l'expansió post-newtoniana, un mètode iteratiu en el qual una solució inicial es corregeix gradualment. Més recentment, s'ha fet possible resoldre l'equació de camp d'Einstein utilitzant un ordinador en comptes de fórmules matemàtiques. Quan els dos cossos orbiten entre si, emeten radiació gravitatòria; això fa que perdin energia i moment angular gradualment, tal com il·lustra el púlsar binari PSR B1913+16.

Per als forats negres binaris, la solució numèrica del problema dels dos cossos es va aconseguir després de quatre dècades d'investigació el 2005, quan tres grups van idear tècniques innovadores.

Context històric

Figura 1. Trajecte el·líptic típic d'una massa més petita m que orbita una massa molt més gran M. La massa més gran també es mou en una òrbita el·líptica, però és massa petita per ser vista perquè M és molt més gran que m. Els extrems del diàmetre indiquen els absides, els punts de distància més propera i més llunyana.

Problema clàssic de Kepler

El problema de Kepler deriva el seu nom de Johannes Kepler, que va treballar com a assistent de l' astrònom danès Tycho Brahe. Brahe va prendre mesures extraordinàriament precises del moviment dels planetes del Sistema Solar. A partir d'aquestes mesures, Kepler va poder formular les lleis de Kepler, la primera descripció moderna del moviment planetari:

1. L' òrbita de cada planeta és una el·lipse amb el Sol en un dels dos focus.
2. Una línia que uneix un planeta i el Sol escombra àrees iguals durant intervals de temps iguals.
3. El quadrat del període orbital d'un planeta és directament proporcional al cub del semieix major de la seva òrbita.

Kepler va publicar les dues primeres lleis el 1609 i la tercera llei el 1619. Van substituir els models anteriors del Sistema Solar, com els de Ptolemeu i Copèrnic. Les lleis de Kepler només s'apliquen en el cas limitat del problema dels dos cossos. Voltaire i Émilie du Châtelet van ser els primers a anomenar-les "lleis de Kepler".

Gairebé un segle més tard, Isaac Newton havia formulat les seves tres lleis del moviment. En particular, la segona llei de Newton estableix que una força F aplicada a una massa m produeix una acceleració a donada per l'equació F = ma. Llavors Newton va plantejar la pregunta: quina ha de ser la força que produeix les òrbites el·líptiques vistes per Kepler? La seva resposta va venir en la seva llei de gravitació universal, que estableix que la força entre una massa M i una altra massa m ve donada per la fórmula $$F=G{\frac {Mm}{r^{2}}},$$ on r és la distància entre les masses i G és la constant gravitatòria. Tenint en compte aquesta llei de forces i les seves equacions de moviment, Newton va ser capaç de demostrar que dues masses puntuals que s'atreuen entre elles seguirien cadascuna òrbites perfectament el·líptiques. La relació de mides d'aquestes el·lipses és m / M, amb la massa més gran movent-se en una el·lipse més petita. Si M és molt més gran que m, llavors la massa més gran semblarà estacionària al focus de l'òrbita el·líptica de la massa més lleugera m. Aquest model es pot aplicar aproximadament al Sistema Solar. Com que la massa del Sol és molt més gran que la dels planetes, la força que actua sobre cada planeta es deu principalment al Sol; la gravetat dels planetes entre si es pot descuidar en primera aproximació.

En absència de cap altra força, una partícula que orbita una altra sota la influència de la gravetat newtoniana segueix eternament la mateixa el·lipse perfecta. La presència d'altres forces (com la gravitació d'altres planetes), fa que aquesta el·lipse giri gradualment. La velocitat d'aquesta rotació (anomenada precessió orbital) es pot mesurar amb molta precisió. La velocitat també es pot predir coneixent les magnituds i direccions de les altres forces. Tanmateix, les prediccions de la gravetat newtoniana no coincideixen amb les observacions, tal com es va descobrir el 1859 a partir d'observacions de Mercuri.

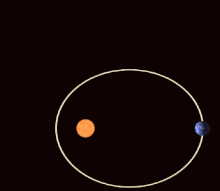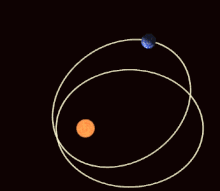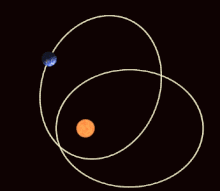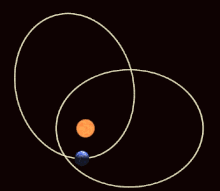
Precessió absidal

Si l'energia potencial entre els dos cossos no és exactament el potencial 1/ r de la llei gravitatòria de Newton, però només difereix lleugerament, aleshores l'el·lipse de l'òrbita gira gradualment (entre altres possibles efectes). Aquesta precessió absidal s'observa per a tots els planetes que orbiten al voltant del Sol, principalment a causa de l'oblat del Sol (no és perfectament esfèric) i les atraccions dels altres planetes entre si. Els absides són els dos punts de distància més propera i més llunyana de l'òrbita (el periapsi i l'apoapsis, respectivament); La precessió absidal correspon a la rotació de la línia que uneix els absids. També correspon a la rotació del vector Laplace–Runge–Lenz, que apunta al llarg de la línia dels àbsides.

La llei de la gravitació de Newton aviat es va acceptar perquè donava prediccions molt precises del moviment de tots els planetes. Aquests càlculs van ser realitzats inicialment per Pierre-Simon Laplace a finals del segle XVIII, i refinats per Félix Tisserand a finals del segle XIX. Per contra, si la llei de la gravitació de Newton no prediria les precessions absidals dels planetes amb precisió, s'hauria de descartar com a teoria de la gravitació. Una precessió tan anòmala es va observar a la segona meitat del segle XIX.

Precessió anòmala de Mercuri

El 1859, Urbain Le Verrier va descobrir que la precessió orbital del planeta Mercuri no era del tot el que hauria de ser; l'el·lipse de la seva òrbita girava (processava) una mica més ràpid del que prediria la teoria tradicional de la gravetat newtoniana, fins i tot després que s'haguessin comptat amb tots els efectes dels altres planetes. L'efecte és petit (aproximadament 43 segons d'arc de rotació per segle), però molt per sobre de l'error de mesura (aproximadament 0,1 segons d'arc per segle). Le Verrier es va adonar de la importància del seu descobriment immediatament i va desafiar tant als astrònoms com als físics a explicar-ho. Es van proposar diverses explicacions clàssiques, com la pols interplanetària, l'oblat no observat del Sol, una lluna no detectada de Mercuri o un nou planeta anomenat Vulcà. Després de descartar aquestes explicacions, alguns físics es van veure conduïts a la hipòtesi més radical que la llei de gravitació del quadrat invers de Newton era incorrecta. Per exemple, alguns físics van proposar una llei de potència amb un exponent que era lleugerament diferent de 2.

Les mesures de 1919 d' Eddington de la flexió de la llum de les estrelles per la gravetat del Sol van portar a l'acceptació de la relativitat general a tot el món.

Teoria de la relativitat general d'Einstein

Al voltant de 1904–1905, els treballs de Hendrik Lorentz, Henri Poincaré i, finalment, la teoria especial de la relativitat d'Albert Einstein, exclouen la possibilitat de propagació de qualsevol efecte més ràpid que la velocitat de la llum. Va seguir que la llei de la gravitació de Newton s'hauria de substituir per una altra llei, compatible amb el principi de relativitat, tot obtenint el límit newtonià per a circumstàncies en què els efectes relativistes són insignificants. Aquests intents els van fer Henri Poincaré (1905), Hermann Minkowski (1907) i Arnold Sommerfeld (1910). El 1907 Einstein va arribar a la conclusió que per aconseguir-ho era necessari un successor de la relativitat especial. De 1907 a 1915, Einstein va treballar cap a una nova teoria, utilitzant el seu principi d'equivalència com a concepte clau per guiar el seu camí. Segons aquest principi, un camp gravitatori uniforme actua per igual sobre tot el que hi ha dins i, per tant, no pot ser detectat per un observador en caiguda lliure. Per contra, tots els efectes gravitatoris locals haurien de ser reproduïbles en un marc de referència d'acceleració lineal, i viceversa. Així, la gravetat actua com una força fictícia com la força centrífuga o la força de Coriolis, que resulten d'estar en un marc de referència accelerat; totes les forces fictícies són proporcionals a la massa inercial, igual que la gravetat. Per efectuar la reconciliació de la gravetat i la relativitat especial i per incorporar el principi d'equivalència, calia sacrificar alguna cosa; que alguna cosa era l'assumpció clàssica de llarga durada que el nostre espai obeeix les lleis de la geometria euclidiana, per exemple, que el teorema de Pitàgores és cert experimentalment. Einstein va utilitzar una geometria més general, la geometria pseudo-riemanniana, per permetre la curvatura de l'espai i el temps que era necessària per a la reconciliació; després de vuit anys de treball (1907–1915), va aconseguir descobrir la manera precisa en què s'havia de corbar l'espai-temps per tal de reproduir les lleis físiques observades a la natura, especialment la gravitació. La gravetat és diferent de les forces fictícies, la força centrífuga i la força de coriolis, en el sentit que la curvatura de l'espai-temps es considera físicament real, mentre que les forces fictícies no es consideren forces. Les primeres solucions de les seves equacions de camp van explicar la precessió anòmala de Mercuri i van predir una flexió inusual de la llum, que es va confirmar després de la publicació de la seva teoria. Aquestes solucions s'expliquen a continuació.

Relativitat general, relativitat especial i geometria

En la geometria euclidiana normal, els triangles obeeixen al teorema de Pitàgores, que estableix que la distància quadrada ds ² entre dos punts de l'espai és la suma dels quadrats de les seves components perpendiculars. $$ds^{2}=dx^{2}+dy^{2}+dz^{2}$$ on dx, dy i dz representen les diferències infinitesimals entre les coordenades x, y i z de dos punts en un sistema de coordenades cartesianes. Ara imagineu-vos un món en què això no sigui del tot cert; un món on la distància ve donada per $$ds^{2}=F(x,y,z)\,dx^{2}+G(x,y,z)\,dy^{2}+H(x,y,z)\,dz^{2}$$ on F, G i H són funcions arbitràries de posició. No és difícil imaginar un món així; vivim d'un. La superfície de la terra és corba, per això és impossible fer un mapa pla de la terra perfectament precís. Els sistemes de coordenades no cartesianes ho il·lustren bé; per exemple, a les coordenades esfèriques ( r, θ, φ ), la distància euclidiana es pot escriure $$ds^{2}=dr^{2}+r^{2}\,d\theta ^{2}+r^{2}\sin ^{2}\theta \,d\varphi ^{2}$$Una altra il·lustració seria un món en què els governants que solien mesurar la longitud eren poc fiables, governants que canviaven la seva longitud amb la seva posició i fins i tot la seva orientació. En el cas més general, cal tenir en compte termes creuats en calcular la distància ds $$ds^{2}=g_{xx}\,dx^{2}+g_{xy}\,dx\,dy+g_{xz}\,dx\,dz+\cdots +g_{zy}\,dz\,dy+g_{zz}\,dz^{2}$$ on les nou funcions g _xx, g _xy,... , g _zz constitueixen el tensor mètric, que defineix la geometria de l'espai en la geometria riemanniana. A l'exemple de coordenades esfèriques anterior, no hi ha termes creuats; els únics components tensors mètrics diferents de zero són g _rr = 1, g _θθ = r ² i g _φφ = r ² sin ² θ.

En la seva teoria especial de la relativitat, Albert Einstein va demostrar que la distància ds entre dos punts espacials no és constant, sinó que depèn del moviment de l'observador. Tanmateix, hi ha una mesura de separació entre dos punts de l'espai-temps —anomenada “temps propi” i denotada amb el símbol dτ — que és invariant; és a dir, no depèn del moviment de l'observador. $$c^{2}\,d\tau ^{2}=c^{2}\,dt^{2}-dx^{2}-dy^{2}-dz^{2}$$ que es pot escriure en coordenades esfèriques com $$c^{2}\,d\tau ^{2}=c^{2}\,dt^{2}-dr^{2}-r^{2}\,d\theta ^{2}-r^{2}\sin ^{2}\theta \,d\varphi ^{2}$$Aquesta fórmula és l'extensió natural del teorema de Pitàgores i de la mateixa manera només s'aplica quan no hi ha curvatura en l'espai-temps. En la relativitat general, però, l'espai i el temps poden tenir curvatura, de manera que aquesta fórmula de distància s'ha de modificar a una forma més general. $$c^{2}\,d\tau ^{2}=g_{\mu \nu }dx^{\mu }\,dx^{\nu }$$ de la mateixa manera que vam generalitzar la fórmula per mesurar la distància a la superfície de la Terra. La forma exacta de la mètrica g _μν depèn de la massa gravitatòria, el moment i l'energia, tal com descriuen les equacions de camp d'Einstein. Einstein va desenvolupar aquestes equacions de camp per coincidir amb les lleis de la natura conegudes aleshores; tanmateix, van predir fenòmens inèdits (com la flexió de la llum per la gravetat) que es van confirmar més tard.