Producte de Hadamard de matrius

El producte de Hadamard opera únicament sobre matrius de la mateixa mida, produint una tercera matriu que també té les mateixes dimensions.

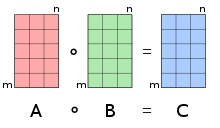
En matemàtiques, el producte de Hadamard (també conegut com a producte element a element o producte de Schur) és una operació binària que pren dues matrius de les mateixes dimensions i produeix una altra matriu de la mateixa dimensió, on cada element i, j és el producte dels elements i, j de les dues matrius originals. No s'ha de confondre amb el producte de matrius habitual. El producte de Hadamard és atribuït al matemàtic francès Jacques Hadamard i al matemàtic alemany Issai Schur, dels quals rep el nom.

El producte de Hadamard és associatiu i distributiu. A diferència del producte matricial, també és commutatiu.

Definició

Donades dues matrius A i B, ambdues de mida m × n, es defineix el producte de Hadamard $A\circ B$ (o $A\odot B$) com la matriu m × n que té per elements el producte dels elements corresponents de A i Bː

$(A\circ B)_{ij}=(A\odot B)_{ij}=(A)_{ij}(B)_{ij}.$

Si A i B són matrius de dimensions diferents (és a dir, A és una matriu m × n i B és una matriu p x q, on m ≠ p o n ≠ q), aleshores el producte de Hadamard

$A\circ B$ no està definit.

Exemple

Per exemple, el producte de Hadamard de dues matrius A i B de dimensions 3 × 3 és

${\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}\circ {\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix}}={\begin{bmatrix}a_{11}\,b_{11}&a_{12}\,b_{12}&a_{13}\,b_{13}\\a_{21}\,b_{21}&a_{22}\,b_{22}&a_{23}\,b_{23}\\a_{31}\,b_{31}&a_{32}\,b_{32}&a_{33}\,b_{33}\end{bmatrix}}.$

Propietats

• El producte de Hadamard és commutatiu (sempre que els elements de les matrius formin part d'un anell commutatiu), associatiu i distributiu respecte la suma. És a dir, si A, B, i C són matrius de la mateixa mida, i k és un escalar, es compleix que

  ${\begin{aligned}{A}\circ {B}&={B}\circ {A},\\{A}\circ ({B}\circ {C})&=({A}\circ {B})\circ {C},\\{A}\circ ({B}+{C})&={A}\circ {B}+{A}\circ {C},\\\left(k{A}\right)\circ {B}&={A}\circ \left(k{B}\right)=k\left({A}\circ {B}\right),\\{A}\circ {0}&={0}\circ {A}={0}.\end{aligned}}$

• La matriu identitat sota el producte de Hadamard de dues matrius m × n és una matriu m × n on tots els elements són iguals a 1. Així doncs, és diferent de la matriu identitat sota el producte de matrius habitual, on només els elements de la diagonal principal són iguals a 1. A més a més, tenim que una matriu té invers sota el producte de Hadamard si i només si cap dels seus elements és igual a zero.
• Donats dos vectors x i y, i les matrius diagonals corresponents D_x i D_y que tenen aquests vectors com a diagonals principals, es compleix la identitat següent:

  $\mathbf {x} ^{*}({A}\circ {B})\mathbf {y} =\operatorname {tr} \left({D}_{\mathbf {x} }^{*}{A}{D}_{\mathbf {y} }{B}^{\mathsf {T}}\right),$ on x^* denota el conjugat transposat de x. En particular, prenent x i y com a vectors d'uns, la fórmula anterior ens indica que la suma de tots els elements del producte de Hadamard $A\circ B$ és la traça d'AB^T, on el superíndex T denota la matriu transposada. Per matrius A i B quadrades tenim un resultat relacionat, que és que les sumes per fila del producte de Hadamard són iguals als elements diagonals d'AB^T:

  $\sum _{i}(A\circ B)_{ij}=\left(B^{\mathsf {T}}A\right)_{jj}=\left(AB^{\mathsf {T}}\right)_{ii}.$

  Similarment,

  $\left(\mathbf {y} \mathbf {x} ^{*}\right)\circ {A}={D}_{\mathbf {y} }{A}{D}_{\mathbf {x} }^{*}$

• El producte de Hadamard és una submatriu principal del producte de Kronecker.
• El producte de Hadamard satisfà la desigualtat de rang

  $\operatorname {rang} ({A}\circ {B})\leq \operatorname {rang} ({A})\operatorname {rang} ({B})$

• Si A i B són matrius definides positives, llavors la desigualtat següent és vàlida:

  $\prod _{i=k}^{n}\lambda _{i}({A}\circ {B})\geq \prod _{i=k}^{n}\lambda _{i}({A}{B}),\quad k=1,\ldots ,n,$ on λ_i(A) és el i-èssim valor propi més gran d'A.

• Si D i E són matrius diagonals, aleshores

  ${\begin{aligned}{D}({A}\circ {B}){E}&=({D}{A}{E})\circ {B}=({D}{A})\circ ({B}{E})\\&=({A}{E})\circ ({D}{B})={A}\circ ({D}{B}{E}).\end{aligned}}$

• El producte de Hadamard de dos vectors $\mathbf {a}$ i $\mathbf {b}$ és el mateix que el producte de matrius habitual d'un dels vectors per la matriu diagonal corresponent de l'altre vector:

  $\mathbf {a} \circ \mathbf {b} =D_{\mathbf {a} }\mathbf {b} .$

La propietat del producte mixt

$(A\otimes B)\circ (C\otimes D)=(A\circ C)\otimes (B\circ D)$, on $\otimes$ denota el producte de Kronecker.

$(A\bullet B)\circ (C\bullet D)=(A\circ C)\bullet (B\circ D)$, on $\bullet$ denota el producte de Khatri-Rao per files.

$(A\bullet B)(C\ast D)=(AC)\circ (BD)$, on $\ast$ denota el producte de Khatri–Rao per columnes.

Teorema del producte de Schur

El producte de Hadamard de dues matrius semidefinides positives dona com a resultat una altra matriu semidefinida positiva. Aquest resultat es coneix com el teorema del producte de Schur, en honor del matemàtic rus Issai Schur. Per dues matrius semidefinides positives A i B, també es sap que el determinant del seu producte de Hadamard és més gran o igual que el producte dels seus determinants respectius:

$\det({A}\circ {B})\geq \det({A})\det({B}).$

En llenguatges de programació

El producte de Hadamard ve implementat a alguns llenguatges de programació sota diversos noms. A MATLAB, Octave, GAUSS i HP Prime, rep el nom de producte d'arrays, i a Julia s'anomena producte d'expansió, amb el símbol .*. A Fortran, R, APL, J i Wolfram (Mathematica), el producte de Hadamard es representa amb l'operador *, mentre que el producte matricial habitual es representa amb la funció matmul, i els operadors %*%, +.×, +/ .* i ., respectivament. A Python, dins de la llibreria NumPy, al multiplicar dos arrays amb a*b obtenim el producte de Hadamard, mentre que a@b representa el producte matricial habitual. Amb la llibreria simbòlica SymPy, el producte de dos arrays tant mitjançant a*b com amb a@b dona el producte matricial, i el producte de Hadamard s'obté amb a.multiply_elementwise(b). A C++, la llibreria Eigen conté la funció cwiseProduct per a la classe Matrix (per exemple, a.cwiseProduct(b)), mentre que la llibreria Armadillo utilitza l'operador % per obtenir l'expressió compacte a%b (a*b és el producte habitual de matrius). El paquet informàtic matrixcalc de R introdueix la funció hadamard.prod() per a realitzar el producte de Hadamard de matrius i vectors numèricament.

Aplicacions

El producte de Hadamard s'utilitza en algoritmes de compressió amb pèrdues com el JPEG. El pas de descodificació implica un producte element a element, és a dir, el producte de Hadamard .

També s'utilitza en el camp de l'aprenentatge automàtic, per exemple per descriure l'arquitectura de xarxes neuronals recurrents com GRUs o LSTMs.

Operacions anàlogues

A la literatura matemàtica també apareixen altres operacions anàlogues al producte de Hadamard com l'arrel de Hadamard o la potència de Hadamard (que de fet són el mateix, ja que una arrel es pot entendre com una potència amb exponent fraccionari). Igual que el producte de Hadamard, aquestes operacions actuen sobre una matriu element a elementː

Potència de Hadamardː

${B}={A}^{\circ 2}\iff B_{ij}={A_{ij}}^{2}$

Arrel de Hadamardː

${B}={A}^{\circ {\frac {1}{2}}}\iff B_{ij}={A_{ij}}^{\frac {1}{2}}$

De la mateixa manera, podem definir la inversa de Hadamard:

${\begin{aligned}{B}&={A}^{\circ -1}\\B_{ij}&={A_{ij}}^{-1}\end{aligned}}$

I també la divisió de Hadamard:

${\begin{aligned}{C}&={A}\oslash {B}\\C_{ij}&={\frac {A_{ij}}{B_{ij}}}\end{aligned}}$

Producte de Hadamard per blocs

El producte de Hadamard per blocs

Segons la definició de Vadym Slyusar, el producte de Hadamard per blocs (en anglès, penetrating face product) és una generalització del producte de Hadamard entre una matriu $A$ de mida p×g i una matriu $B$ que es pot dividir en n blocs de mida p×g ($B=[B_{1}\vert B_{2}\vert \dots \vert B_{n}]$)ː

${A}[\circ ]{B}=\left[{\begin{array}{c | c | c | c }{A}\circ {B}_{1}&{A}\circ {B}_{2}&\cdots &{A}\circ {B}_{n}\end{array}}\right].$

Exemple

Si

${A}={\begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix}},\quad {B}=\left[{\begin{array}{c | c | c }{B}_{1}&{B}_{2}&{B}_{3}\end{array}}\right]=\left[{\begin{array}{c c c | c c c | c c c }1&4&7&2&8&14&3&12&21\\8&20&5&10&25&40&12&30&6\\2&8&3&2&4&2&7&3&9\end{array}}\right]$

aleshores

${A}[\circ ]{B}=\left[{\begin{array}{c c c | c c c | c c c }1&8&21&2&16&42&3&24&63\\32&100&30&40&125&240&48&150&36\\14&64&27&14&32&18&49&24&81\end{array}}\right].$

Propietats principals

${A}[\circ ]{B}={B}[\circ ]{A}$,

${M}\bullet {M}={M}[\circ ]\left({M}\otimes \mathbf {1} ^{\textsf {T}}\right)$,

on $\bullet$ denota el producte de Khatri-Rao per files,

$\mathbf {c} \bullet {M}=\mathbf {c} [\circ ]{M}$, on $\mathbf {c}$ és un vector.

Aplicacions

El producte de Hadamard per blocs s'utilitza en la teoria tensor-matriu de les agrupacions d'antenes digitals. També s'utilitza en models de xarxes neuronals artificials, especialment en capes convolucionals.

Vegeu també

• Producte Kronecker