Segon moment d'àrea

En enginyeria estructural, el segon moment d'àrea, també anomenat segon moment d'inèrcia o moment d'inèrcia d'àrea, és una propietat geomètrica de la secció transversal d'elements estructurals. Físicament el segon moment d'inèrcia està relacionat amb les tensions i deformacions màximes que apareixen per flexió en un element estructural i, per tant, juntament amb les propietats del material determina la resistència màxima d'un element estructural sota flexió.

El segon moment d'àrea és una magnitud les dimensions de la qual són longitud a la quarta potència, normalment cm⁴ i no s'ha de confondre amb el concepte físic relacionat d'inèrcia rotacional, on les unitats són massa per longitud al quadrat). Per evitar confusions, alguns enginyers denominen "moment d'inèrcia de massa" al moment amb unitats de massa descrit en aquell article.

Definició

Donada una secció plana transversal Σ d'un element estructural, el segon moment d'inèrcia es defineix per a cada eix de coordenades contingut en el pla de la secció Σ mitjançant la següent fórmula:

(1) $I_{\rm {eix}}=\iint _{\Sigma }r^{2}dA$

On:

I_eix, és el segon moment d'inèrcia al voltant de l'eix escollit.
dona, és el diferencial d'àrea, de la secció Σ.
r, és la mínima distància de l'element dona a l'eix escollit.

Moments d'inèrcia principals

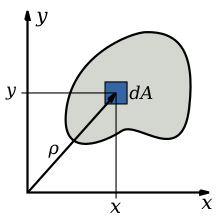
Si considerem novament una secció transversal plana Σ i la parametritzem mitjançant coordenades rectangulars (x,y), llavors podem definir dos moments d'inèrcia associats a la flexió segons x o segons y a més del moment d'inèrcia mitjançant:

(2) ${\begin{cases}I_{x}=\iint _{\Sigma }y^{2}\ dxdy\\I_{y}=\iint _{\Sigma }x^{2}\ dxdy\\I_{xy}=-\iint _{\Sigma }xy\ dxdy=I_{yx}\end{cases}}$

Aquests moments defineixen les components d'un tensor de segon ordre:

(3) $\mathbf {I} ={\begin{bmatrix}I_{x}&I_{xy}\\I_{yx}&I_{y}\end{bmatrix}},\quad \det(\mathbf {I} )>0$

Els eixos es diu que són eixos principals d'inèrcia si $I_{xy}=0$ i en aquest cas podem escriure la tensió perpendicular associada a la flexió desviada simple de l'element estructural sobre cada punt de la secció Σ estudiada com:

(4) $\sigma (x,y)=-{\frac {M_{x}\cdot y}{I_{x}}}+{\frac {M_{y}\cdot x}{I_{y}}}$

Sent M_x i M_y les components del moment flector total sobre la secció Σ. Les unitats en el Sistema Internacional d'Unitats per al segon moment d'inèrcia són longitud a la quarta potència, en la pràctica la majoria de seccions d'ús en enginyeria es donen en (cm⁴). Si els eixos de referència emprats no necessàriament són eixos principals l'expressió completa de la tensió en qualsevol punt genèric ve donada per:

(5) $\sigma (x,y)={\frac {xI_{x}-yI_{xy}}{I_{y}I_{x}-I_{yx}^{2}}}M_{i}+{\frac {yI_{i}-xI_{yx}}{I_{y}I_{x}-I_{xy}^{2}}}M_{x}$

Teorema d'eixos paral·lels

El teorema de Steiner o d'eixos paral·lels permet, coneguts els moments respecte a eixos que passin pel centre de gravetat, calcular molt fàcilment els moments d'inèrcia respecte a eixos paral·lels que no passin pel centre de gravetat. Aquest "trasllat" del segon moment d'inèrcia, es fa mitjançant la fórmula:

(6) $I_{\rm {eix}}=I_{\rm {eix}}^{(CM)}+Ad_{\rm {eix}}^{2}\,$

On:

I_eix - Segon moment d'inèrcia respecte a l'eix que no passa pel centre de massa.

I^(CM)_eix - Segon moment d'inèrcia per a l'eix que passa pel centre de gravetat.

A - Àrea de la secció transversal.

d - Distància entre el nou eix i l'eix que passa pel centre de gravetat.

El resultat anterior es pot generalitzar a totes les components del tensor d'inèrcia :

(7) $I_{ij}=I_{ij}^{(CM)}+Ad_{i}d_{j}\,$

On: $\mathbf {d} =(d_{x},d_{y},d_{z})$ són les coordenades del punt P, on passa el nou eix a recalcular, respecte al centre de masses (CM).

Vegeu també

Llista de moments d'inèrcia d'àrees

Enllaços externs

Apunts de física p.42. Jordi Farjas Silva PDF(català)
Explicació i resolució de problemes Arxivat 2013-07-17 a Wayback Machine. PDF(castellà)