Superfície de fluència

Comparació de les superfícies de fluència per als criteris de Von Mises i Tresca a usant les tensions principals com coordenades.

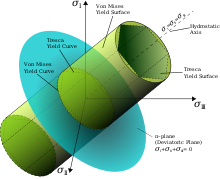
La superfície de fluència d'un material és una construcció abstracta que permet visualitzar el conjunt de tensions possibles o admissibles dins d'un sòlid deformable elastoplàstic.

Introducció

L'estat tensional d'un cos pot caracteritzar mitjançant tres valors de tensió segons tres direccions perpendiculars conegudes com a tensions principals de tensió, sent els tres valors de tensió les trucades tensions principals. Per això així l'estat tensional en aquest punt pot representar-se per un espai tridimensional $\mathbb {R} ^{3}$. La superfície de fluència és una superfície bidimensional en aquest espai de tensions.

Quan un sòlid deformable se sotmet a tensions progressivament grans, l'energia potencial elàstica s'incrementa fins a cert punt el qual es produeixen transformacions termodinàmiques irreversibles en superar aquesta energia de cert valor. El conjunt de punts per sota dels quals no es produeixen transformacions termodinàmiques irreversibles és el conjunt de tensions admissibles. És una regió connexa de l'espai de tensions. La frontera de la regió de tensions admissibles és precisament superfície de fluència.

Plasticitat perfecta

Un material elastoplàstic es diu que presenta plasticitat perfecta, sigui quin sigui el valor de les tensions en un punt, la superfície de fluència no canvia de forma ni de posició en l'espai abstracte de tensions. Quan un material presenta plasticitat perfecta, les equacions constitutives no necessiten incloure variables internes ni esforços conjugats associats i el problema elastoplàstic és més senzill.

Els experimentals en canvi presenten gairebé sempre plasticitat imperfecta, i la superfície de fluència pot patir desplaçaments, tal com succeeix en l'efecte Bauschinger. Els canvis de forma, generalment estan associats al comportament d'enduriment, augmentant en aquest cas el volum tancat a la superfície de fluència.

Propietats de la superfície de fluència

• Convexitat : Sota arguments termodinàmics pot provar-se que, la superfície de fluència és convexa.
• Compacitat : La superfície de fluència es considera tancada i per tant tanca un volum finit. I per tant el conjunt de tensions assolibles és sempre un conjunt compacte.
• Continuïtat : La superfiecie de fluència es considera que és Lipshitz-contínua.
• Unicitat del problema elastopolàstic ': Quan la superfície no és diferenciable el problema elastoplàstic pot ser tractat mitjançant mètodes variacionals. Sota condicions prou regulars pot provar que la solució del problema elastoplàstic, encara que la superfície no sigui diferenciable, és única.

Bibliografia

• Weimin Han & B. Daya Reddy: Plasticity: Mathematical Theory and Numerical Analysis , Springer-Verlag, Nova York, 1999, ISBN 0-387-98704-5.