Teorema de Sylvester-Gallai
El teorema de Sylvester-Gallai estableix que donat un conjunt finit de punts no alineats en el pla euclidià, existeix una recta que conté exactament dos dels punts.[1]
Aquest enunciat el va proposar el matemàtic anglès James Joseph Sylvester el 1893. Ho va fer en forma de problema a una columna de la revista Educational Times. Uns quaranta anys després, Tibor Gallai, un matemàtic hongarès, va demostrar el teorema.[1]
Demostració
[modifica]Hi ha hagut altres demostracions posteriors a la de Gallai, d'entre les quals destaca per la seva senzillesa la del matemàtic nord-americà Leroy Milton Kelly,[1] que s'explica a continuació.
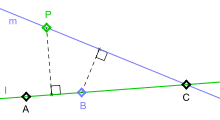
Sigui K el conjunt de punts donat. Anomenem L el conjunt de totes les rectes que passen per un mínim de dos punts de K. D'entre totes les parelles formades per un punt i una recta d'aquests conjunts tals que el punt no pertany a la recta, n'escollim la parella (P,l) tal que la distància entre P i l sigui la més petita. Anomenem P' la projecció del punt P sobre la recta l, que és el punt d'intersecció entre l i una recta perpendicular a l que passa per P.
Suposem que la recta l conté un mínim de tres punts de K: A, B i C. Com a mínim dos d'ells han d'estar cap al mateix costat de P'; els podem anomenar B i C de més proper a més llunyà. També pot ser que B coincideixi amb P', però això no suposa cap complicació afegida. Considerem la recta m que passa per P i C i que, per definició, pertany a K. Es pot demostrar que la distància entre B i m és més petita que la distància entre P i l, cosa que suposa una contradicció amb l'elecció de la parella (P,l), que havia de tenir la distància més petita. Així doncs, la suposició que hem fet no pot ser certa, perquè ens porta a una contradicció. La recta l conté, per tant, exactament dos dels punts de K. Això demostra el teorema.
Referències
[modifica]- ↑ 1,0 1,1 1,2 Aigner, Martin; Ziegler, Günter M. «Capítulo 9: Rectas en el plano y descomposicion de grafos». A: El Libro de las demostraciones (en castellà). Editorial Nivola. ISBN 84-95599-95-3 [Consulta: 22 maig 2010].
