Teoria del cable

Figura. 1: visió simplificada de la teoria del cable d'una fibra neuronal

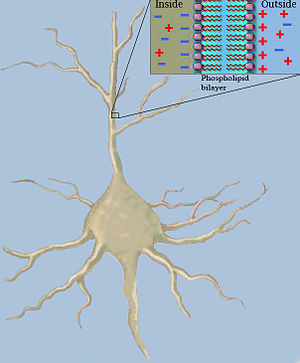
La teoria clàssica del cable utilitza models matemàtics per calcular el corrent elèctric (i la tensió que l'acompanya) al llarg de les neurites passives, particularment les dendrites que reben entrades sinàptiques en diferents llocs i moments. Les estimacions es fan modelant dendrites i axons com a cilindres composts per segments amb capacitats. $c_{m}$ i resistències $r_{m}$ combinats en paral·lel (vegeu la figura 1). La capacitat d'una fibra neuronal es produeix perquè les forces electroestàtiques actuen a través de la bicapa lipídica molt prima (vegeu la figura 2). La resistència en sèrie al llarg de la fibra $r_{l}$ es deu a la important resistència de l'axoplasma al moviment de la càrrega elèctrica.

Història

La teoria del cable en la neurociència computacional té arrels que es remunten a la dècada de 1850, quan el professor William Thomson (més tard conegut com Lord Kelvin) va començar a desenvolupar models matemàtics de decadència del senyal en cables telegràfics submarins (submarins). Els models s'assemblaven a les equacions diferencials parcials utilitzades per Fourier per descriure la conducció de calor en un cable.

Figura. 2: Capacitat de fibra

La dècada de 1870 va veure els primers intents de Hermann de modelar els potencials electrotònics neuronals també centrant-se en analogies amb la conducció de calor. Tanmateix, va ser Hoorweg qui va descobrir per primera vegada les analogies amb els cables submarins de Kelvin el 1898 i després Hermann i Cremer els qui van desenvolupar de manera independent la teoria del cable per a fibres neuronals a principis del segle XX. Cole i Hodgkin (1920-1930), Offner et al. van desenvolupar altres teories matemàtiques de la conducció de fibres nervioses basades en la teoria del cable. (1940) i Rushton (1951).

Derivació de l'equació del cable

Tingueu en compte que existeixen diverses convencions de r_m. Aquí r_m i c_m, tal com s'ha introduït anteriorment, es mesuren per unitat de longitud de membrana (per metre (m)). Així, r_m es mesura en ohm ·metres (Ω·m) i c_m en farads per metre (F/m). Això contrasta amb R_m (en Ω·m ² ) i C_m (en F/m ² ), que representen la resistència específica i la capacitat, respectivament, d'una unitat d'àrea de membrana (en m²). Així, si es coneix el radi, a, de l'axó, aleshores la seva circumferència és 2 πa, i la seva r_m, i els seus valors c _m es poden calcular com:

$r_{m}={\frac {R_{m}}{2\pi a\ }}$

(1)

$c_{m}=C_{m}2\pi a\$

(2)

Aquestes relacions tenen sentit intuïtivament, perquè com més gran és la circumferència de l'axó, més gran és l'àrea de càrrega per escapar a través de la seva membrana i, per tant, menor és la resistència de la membrana (dividint R_m per 2 πa); i més membrana disponible per emmagatzemar càrrega (multiplicant C_m per 2 πa). La resistència elèctrica específica, ρ _l, de l'axoplasma permet calcular la resistència intracel·lular longitudinal per unitat de longitud, r_l, (en Ω·m ⁻¹ ) per l'equació:

$r_{l}={\frac {\rho _{l}}{\pi a^{2}\ }}$

(3)

Per entendre millor com es deriva l'equació del cable, primer simplifiqueu encara més la neurona teòrica i pretengueu que té una membrana perfectament segellada (r_m =∞) sense pèrdua de corrent cap a l'exterior i sense capacitat (c_m = 0). Un corrent injectat a la fibra a la posició x = 0 es mourà per l'interior de la fibra sense canvis. Allunyant-se del punt d'injecció i utilitzant la llei d'Ohm (V = IR ) podem calcular el canvi de tensió com:

$\Delta V=-i_{l}r_{l}\Delta x\$

(4)

Si deixem que Δ x vagi cap a zero i tenint increments infinitament petits de x, es pot escriure (4 ) com:

${\frac {\partial V}{\partial x}}=-i_{l}r_{l}\$

(5)

o

${\frac {1}{r_{l}}}{\frac {\partial V}{\partial x}}=-i_{l}\$

(6)

Si i _m és el corrent que escapa a través de la membrana per unitat de longitud, m, aleshores el corrent total que escapa al llarg de y unitats ha de ser y·i _m . Així, el canvi de corrent a l'axoplasma, Δ i _l, a distància, Δ x, des de la posició x =0 es pot escriure com:

$\Delta i_{l}=-i_{m}\Delta x\$

(7)

o, utilitzant increments continus i infinitesimament petits:

${\frac {\partial i_{l}}{\partial x}}=-i_{m}\$

(8)

$i_{m}$ es pot expressar amb una altra fórmula, incloent la capacitat. La capacitat provocarà un flux de càrrega (un corrent) cap a la membrana del costat del citoplasma. Aquest corrent es coneix normalment com a corrent de desplaçament (aquí es denota $i_{c}$). El flux només es produirà mentre no s'hagi arribat a la capacitat d'emmagatzematge de la membrana. $i_{c}$ llavors es pot expressar com:

$i_{c}=c_{m}{\frac {\partial V}{\partial t}}\$

(9)

on $c_{m}$ és la capacitat de la membrana i ${\partial V}/{\partial t}$ és el canvi de tensió al llarg del temps. El corrent que passa per la membrana ($i_{r}$ ) es pot expressar com:

$i_{r}={\frac {V}{r_{m}}}$

(10)

i perquè $i_{m}=i_{r}+i_{c}$ la següent equació per $i_{m}$ es pot derivar si no s'afegeix cap corrent addicional des d'un elèctrode:

${\frac {\partial i_{l}}{\partial x}}=-i_{m}=-\left({\frac {V}{r_{m}}}+c_{m}{\frac {\partial V}{\partial t}}\right)$

(11)

on ${\partial i_{l}}/{\partial x}$ representa el canvi per unitat de longitud del corrent longitudinal.

La combinació de les equacions (6) i (11) dona una primera versió d'una equació de cable:

${\frac {1}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}{\frac {\partial V}{\partial t}}+{\frac {V}{r_{m}}}$

(12)

que és una equació diferencial parcial de segon ordre (PDE).

Mitjançant una simple reordenació de l'equació (12) és possible fer aparèixer dos termes importants, és a dir, la constant de longitud (de vegades anomenada constant espacial) denotada $\lambda$ i la constant de temps indicada $\tau$.

${\frac {r_{m}}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}r_{m}{\frac {\partial V}{\partial t}}+V$

(19)

i reconèixer $\lambda ^{2}={r_{m}}/{r_{l}}$ al costat esquerre i $\tau =c_{m}r_{m}$ al costat dret. L'equació del cable ara es pot escriure en la seva forma potser més coneguda:

$\lambda ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}=\tau {\frac {\partial V}{\partial t}}+V$

(20)

Aquesta és una equació de calor 1D o equació de difusió per a la qual s'han desenvolupat molts mètodes de solució, com ara les funcions de Green i els mètodes de Fourier.

També és un cas especial degenerat de l'equació del telègraf, on la inductància $L$ s'esvaeix i la velocitat de propagació del senyal $1/{\sqrt {LC}}$ és infinit.