Trajectòria terrestre

Una trajectòria terrestre (de l'anglès ground track) és la trajectòria a la superfície d'un planeta directament per sota de la trajectòria d'una aeronau o satèl·lit. En el cas dels satèl·lits, també se'l coneix com a pista suborbital, i és la projecció vertical de l'òrbita del satèl·lit sobre la superfície de la Terra (o qualsevol cos que estigui orbitant el satèl·lit).^[1]

Es pot pensar que una trajectòria terrestre de satèl·lit és un camí al llarg de la superfície terrestre que traça el moviment d'una línia imaginària entre el satèl·lit i el centre de la Terra. En altres paraules, la trajectòria terrestre és el conjunt de punts on el satèl·lit passarà directament per sobre, o creuarà el zenit, en el sistema de referència d'un observador terrestre.^[2]

Trajectòries terrestres d'avions

En la navegació aèria, les pistes terrestres solen aproximar-se a un arc d'un gran cercle, sent aquesta la distància més curta entre dos punts de la superfície terrestre. Per seguir una pista de terra especificada, un pilot ha d'ajustar el seu rumb per compensar l'efecte del vent. Les rutes d'avions estan planejades per evitar l'espai aeri restringit i les zones perilloses, i per passar prop de les balises de navegació.

Trajectòries terrestres per satèl·lit

La trajectòria terrestre d'un satèl·lit pot adoptar diverses formes, depenent dels valors dels elements orbitals, paràmetres que defineixen la mida, la forma i l'orientació de l'òrbita del satèl·lit. (Aquest article tracta sobre òrbites tancades o òrbites amb excentricitat inferior a una i, per tant, exclou les trajectòries parabòliques i hiperbòliques).

Moviment directe i retrògrad

Normalment, els satèl·lits tenen una trajectòria terrestre aproximadament sinusoïdal. Es diu que un satèl·lit amb una inclinació orbital entre zero i noranta graus es troba en el que s'anomena directa o òrbita prògrada, és a dir, orbita en la mateixa direcció que la rotació del planeta. Es diu que un satèl·lit amb una inclinació orbital entre 90° i 180° (o, de manera equivalent, entre 0° i −90°) es troba en una òrbita retrògrada. (Les òrbites directes són, amb diferència, les més comunes per als satèl·lits artificials, ja que la velocitat inicial impartida per la rotació de la Terra en el llançament redueix el delta-v necessari per aconseguir l'òrbita).

Un satèl·lit en òrbita directa amb un període orbital inferior a un dia tendirà a moure's d'oest a est al llarg de la seva trajectòria terrestre. Això s'anomena moviment "directe aparent". Un satèl·lit en òrbita directa amb un període orbital superior a un dia tendirà a moure's d'est a oest al llarg de la seva trajectòria terrestre, en el que s'anomena moviment "aparent retrògrad". Aquest efecte es produeix perquè el satèl·lit orbita més lentament que la velocitat a la qual gira la Terra per sota d'ell. Qualsevol satèl·lit en una òrbita retrògrada veritable es mourà sempre d'est a oest al llarg de la seva ruta terrestre, independentment de la durada del seu període orbital.

Com que un satèl·lit en una òrbita excèntrica es mou més ràpidament prop del perigeu i més lentament prop de l'apogeu, és possible que un satèl·lit segueixi cap a l'est durant una part de la seva òrbita i cap a l'oest durant una altra part. Aquest fenomen permet trajectòries terrestres que es creuen sobre si mateixes en una única òrbita, com en les òrbites geosincròniques i Molniya que s'analitzen a continuació.

Efecte del període orbital

Una òrbita geoestacionària vista des de dalt del pol nord

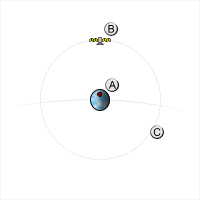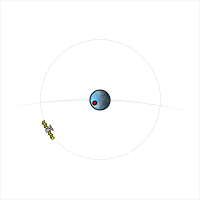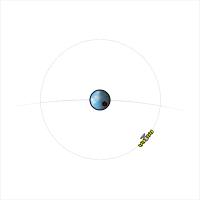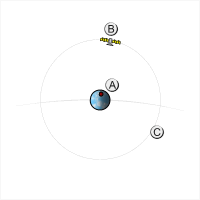
Un satèl·lit el període orbital del qual és una fracció sencera d'un dia (per exemple, 24 hores, 12 hores, 8 hores, etc.) seguirà aproximadament la mateixa trajectòria terrestre cada dia. Aquesta trajectòria terrestre es desplaça cap a l'est o l'oest segons la longitud del node ascendent, que pot variar amb el temps degut a les pertorbacions de l'òrbita. Si el període del satèl·lit és una mica més llarg que una fracció sencera del dia, la trajectòria terrestre es desplaçarà cap a l'oest amb el temps; si és una mica més curt, la trajectòria terrestre es desplaçarà cap a l'est.^[2]^[3]

A mesura que augmenta el període orbital d'un satèl·lit, apropant-se al període de rotació de la Terra (és a dir, a mesura que la seva velocitat orbital mitjana s'alenteix cap a la velocitat de rotació de la Terra), la seva pista terrestre sinusoidal es comprimirà longitudinalment, el que significa que els "nodes". "(els punts en què creua l'equador) s'acostaran, fins que a l'òrbita geosincrònica es troben directament l'un sobre l'altre. Per a períodes orbitals més llargs que el període de rotació de la Terra, un augment del període orbital correspon a un estirament longitudinal de la trajectòria terrestre (aparent retrògrada).

Es diu que un satèl·lit el període orbital del qual és "igual" al període de rotació de la Terra està en una òrbita geosíncrona. La seva trajectòria terrestre tindrà una forma de "figura vuit" sobre una ubicació fixa a la Terra, creuant l'equador dues vegades al dia. Seguirà cap a l'est quan estigui a la part de la seva òrbita més propera al perigeu, i cap a l'oest quan estigui més a prop de l'apogeu.

Un cas especial de l'òrbita geosíncrona, l'òrbita geoestacionària, té una excentricitat de zero (és a dir que l'òrbita és circular) i una inclinació de zero en el sistema de coordenades geocèntriques centrat a la Terra i fix a la Terra (és a dir, el pla orbital no està inclinat en ralació a l'equador terrestre). La "trajectòria terrestre" en aquest cas consisteix en un únic punt de l'equador de la Terra, per sobre del qual es troba el satèl·lit en tot moment. Tingueu en compte que el satèl·lit encara està en òrbita al voltant de la Terra; la seva aparent falta de moviment es deu al fet que la Terra gira al voltant del seu propi centre de massa a la mateixa velocitat que el satèl·lit està en òrbita.

Efecte de la inclinació

La inclinació orbital és l'angle format entre el pla d'una òrbita i el pla equatorial de la Terra. Les latituds geogràfiques cobertes per la trajectòria terrestre aniran de –i a i, on i és la inclinació orbital.^[3] En altres paraules, com més gran sigui la inclinació de l'òrbita d'un satèl·lit, més al nord i al sud passarà la seva trajectòria terrestre. Es diu que un satèl·lit amb una inclinació de 90° exactament està en una òrbita polar, és a dir, passa per sobre dels pols nord i sud de la Terra.

Els llocs de llançament a latituds més baixes són sovint preferits en part per la flexibilitat que permeten en la inclinació orbital; la inclinació inicial d'una òrbita es limita a ser superior o igual a la latitud de llançament. Els vehicles llançats des de Cap Canaveral, per exemple, tindran una inclinació orbital inicial d'almenys 28°27′, la latitud del lloc de llançament, i per assolir aquest mínim cal llançar-se amb un azimut cap a l'est, cosa que pot no ser sempre factible donat altres limitacions de llançament. En els extrems, un lloc de llançament situat a l'equador es pot llançar directament a qualsevol inclinació desitjada, mentre que un lloc de llançament hipotètic al pol nord o sud només podria llançar-se a òrbites polars. (Tot i que és possible realitzar una maniobra de canvi d'inclinació orbital un cop a l'òrbita, aquestes maniobres solen estar entre les més costoses, en termes de combustible, de totes les maniobres orbitals, i normalment s'eviten o minimitzen en la mesura que sigui possible).

A més de proporcionar una gamma més àmplia d'inclinacions inicials de l'òrbita, els llocs de llançament a latituds baixes ofereixen l'avantatge de requerir menys energia per fer l'òrbita (almenys per a òrbites prògrades, que comprenen la gran majoria de llançaments), a causa de la velocitat inicial proporcionada per la rotació terrestre. El desig de llocs de llançament equatorials, juntament amb realitats geopolítiques i logístiques, ha fomentat el desenvolupament de plataformes de llançament flotants, sobretot el Sea Launch.

Efecte de l'argument del perigeu

La trajectòria terrestre d'una òrbita de Molniya

Si l'argument del perigeu és zero, el que significa que el perigeu i l'apogeu es troben en el pla equatorial, aleshores la trajectòria terrestre del satèl·lit apareixerà igual per sobre i per sota de l'equador (és a dir, mostrarà 180° de la simetria rotacional sobre els nodes orbitals). Tanmateix, si l'argument del perigeu és diferent de zero, el satèl·lit es comportarà de manera diferent als hemisferis nord i sud. L'òrbita Molniya, amb un argument de perigeu prop de -90°, és un exemple d'aquest cas. En una òrbita Molniya, l'apogeu es produeix a una latitud elevada (63°), i l'òrbita és molt excèntrica (e = 0,72). Això fa que el satèl·lit es "mantingui" per sobre d'una regió de l'hemisferi nord durant molt de temps, mentre passa molt poc temps sobre l'hemisferi sud. Aquest fenomen se'l coneix com "apogeu" i és desitjable per a comunicacions per a regions de latituds altes.^[3]

Repetició d'òrbites

Com que sovint es requereixen operacions orbitals per supervisar una ubicació específica a la Terra, sovint s'utilitzen òrbites que cobreixen la mateixa trajectòria terrestre periòdicament. A la Terra, aquestes òrbites s'anomenen habitualment òrbites de repetició terrestre. Aquestes òrbites utilitzen l'efecte de precessió nodal per desplaçar l'òrbita de manera que la trajectòria terrestre coincideixi amb la d'una òrbita anterior, de manera que això equilibra essencialment el desplaçament de la revolució del cos orbitat. La rotació longitudinal després d'un període determinat d'un planeta ve donada per:

\Delta L_{1}=-2\pi {\frac {T}{T_{E}}}

where

$T$ és el temps transcorregut
$T_{E}$ és el moment d'una revolució completa del cos en òrbita, en el cas de la Terra un dia sideral

L'efecte de la precessió nodal es pot quantificar com:

\Delta L_{2}=-{\frac {3\pi J_{2}R_{e}^{2}cos(i)}{a^{2}(1-e^{2})^{2}}}

on

$J_{2}$ és el segon factor de forma dinàmica del cos
$R_{e}$ és el radi del cos
$i$ és la inclinació orbital
$a$ és el semieix major de l'òrbita
$e$ és l'excentricitat orbital

Aquests dos efectes s'han de cancel·lar després d'un conjunt de revolucions orbitals $j$ i $k$ dies (siderals). Per tant, equiparant el temps transcorregut amb el període orbital del satèl·lit i combinant les dues equacions anteriors s'obté una equació que val per a qualsevol òrbita que sigui una òrbita repetida:

j\left|\Delta L_{1}+\Delta L_{2}\right|=j\left|-2\pi {\frac {2\pi {\sqrt {\frac {a^{3}}{\mu }}}}{T_{E}}}-{\frac {3\pi J_{2}R_{e}^{2}cos(i)}{a^{2}(1-e^{2})^{2}}}\right|=k2\pi

on

$\mu$ és el paràmetre gravitacional estàndard per al cos que està orbitant
$j$ és el nombre de revolucions orbitals després del qual es cobreix la mateixa trajectòria terrestre
$k$ és el nombre de dies siderals després dels quals es cobreix la mateixa trajectòria terrestre

Referències

↑ [1]
↑ ^2,0 ^2,1 Curtis, Howard D. Orbital Mechanics for Engineering Students. 1a. Amsterdam: Elsevier Ltd., 2005. ISBN 978-0-7506-6169-0.
↑ ^3,0 ^3,1 ^3,2 Montenbruck, Oliver; Gill, Eberhard. Springer. Satellite Orbits: Models, Methods, and Applications. 1a, 2000. ISBN 3-540-67280-X.

Bibliografia

Lyle, S.; Capderou, Michel. Springer. Satellites: Orbits and Missions, 2006, p. 175–264. ISBN 9782287274695.

Vegeu també

Estació terrestre
Terminador, la línia mòbil que separa el costat diürn il·luminat i el costat fosc nocturn d'un cos planetari

Enllaços externs

Satellite Tracker at eoPortal.org
satview.org

[1] [1]

[curtis-2] 2,0 ^2,1 Curtis, Howard D. Orbital Mechanics for Engineering Students. 1a. Amsterdam: Elsevier Ltd., 2005. ISBN 978-0-7506-6169-0.

[monty-3] 3,0 ^3,1 ^3,2 Montenbruck, Oliver; Gill, Eberhard. Springer. Satellite Orbits: Models, Methods, and Applications. 1a, 2000. ISBN 3-540-67280-X.

[1]

[2]

[3]