Usuari:Enricbraso/proves/deltaedre

Un deltaedre és un políedre on totes les seves cares són triangles equilàters iguals[1]. S'anomenen així per la lletra grega delta que en majúscules s'escriu com un triangle (Δ). Hi ha infinits deltaedres, però sols vuit són convexos, d'aquests, sols 3 són regulars.
Cares, vèrtexs i arestes als deltaedres
[modifica]Del fet que les cares siguin sempre triangles, es dedueix que el nombre d'arestes és , on és el nombre de cares. Això implica que no hi ha deltaedres amb un nombre senar de cares[2]. La fórmula d'Euler també dona el nombre de vèrtexs en funció de les cares
Analitzant els deltaedres succeeix que apareixen cares contigües coplanars, per exemple si a un vèrtex coincideixen 6 cares. Aquests poliedres amb cares no triangulars o desiguals que es poden subdividir en triangles no es consideren deltaedres en sentit estricte.
Els vuit deltaedres convexos
[modifica]Sols hi ha vuit deltaedres convexos[3][4]: tres són poliedres regulars i cinc sòlids de Johnson.
| Deltaedres regulars | ||||||
|---|---|---|---|---|---|---|
| Imatge | Nom | Cares | Arestes | Vèrtexs | Configuració dels vèrtexs | Grup de simetria |

|
tetraedre | 4 | 6 | 4 | 4 vèrtexs d'ordre 3 (on coincideixen 3 cares) | Td, [3,3] |

|
octaedre | 8 | 12 | 6 | 6 vèrtexs d'ordre 4 (on coincideixen 4 cares) | Oh, [4,3] |

|
icosaedre | 20 | 30 | 12 | 12 vèrtexs d'ordre 5 (on coincideixen 5 cares) | Ih, [5,3] |
| Deltaedres de Johnson | |||||||
|---|---|---|---|---|---|---|---|
| Imatge | Nom | Número de Johnson | Cares | Arestes | Vèrtexs | Configuració dels vèrtexs | Grup de simetria |

|
bipiràmide triangular | J12 | 6 | 9 | 5 | 2 vèrtexs d'ordre 3 3 vèrtexs d'ordre 4 |
D3h, [3,2] |

|
bipiràmide pentagonal | J13 | 10 | 15 | 7 | 5 vèrtexs d'ordre 4 2 vèrtexs d'ordre 5 |
D5h, [5,2] |

|
bisfenoide xato
(dodecàedre siamès) |
J84 | 12 | 18 | 8 | 4 vèrtexs d'ordre 4 4 vèrtexs d'ordre 5 |
D2d, [2,2] |

|
prisma triangular triaugmentat | J51 | 14 | 21 | 9 | 3 vèrtexs d'ordre 4 6 vèrtexs d'ordre 5 |
D3h, [3,2] |

|
bipiàmide quadrada giroallargada | J17 | 16 | 24 | 10 | 2 vèrtexs d'ordre 4 8 vèrtexs d'ordre 5 |
D4d, [4,2] |
Aquests cinc darrers deltaedres no són regulars, ja que tot i tenir totes les cares com a triangles equilàters iguals tenen vèrtexs de diferents tipus. Per exemple la bipiràmide triangular té dos vèrtexs d'ordre 3 on coincideixen tres cares i tres vèrtexs d'ordre 4 on coincideixen 4 cares. Es classifiquen per això dins el grup dels sòlids de Johnson.
Els deltaedres mantenen sempre la seva forma, són rígids. Construïts com a esquelets és a dir sols amb les arestes, no es poden deformar. Aquesta propietat no sempre es compleix, l'esquelet d'un cub, per exemple, es pot deformar com a prisma de base ròmbica o fins i tot quedar aplanat.
Els deltaedres no convexos o còncaus
[modifica]Hi ha infinits deltaedres no convexos, per veure això sols cal imaginar els poliedres que es poden aconseguir enganxant tetraedres iguals.
Alguns dels més simples són els que es mostren a continuació, les possibles cadenes i ramificacions de poliedres enganxats són infinites

|

|

|
| |
| Unió de 3 tetraedres,
8 cares |
Unió de 4 tetraedres,
10 cares |
Unió de 5 tetraedres,
12 cares |
Unió de 8 octaedres,
48 cares |
|---|
Són coneguts els deltaedres generats a partir dels poliedres regulars construint piràmides fetes amb triangles equilàters, enganxades sobre les seves cares

|

|
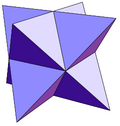
|

|

|
| Poliedre construït amb un tetraedre com a nucli, enganxant 4 tetraedres a les seves cares | Poliedre construït amb un cub de nucli, enganxant 6 piràmides quadrades a les cares | Estel octangle construït amb un octaedre de nucli, enganxant 8 tretraedres a les cares |
Poliedre construït amb un dodecaedre regular de nucli, enganxant 12 piràmides pentagonals a les cares | Poliedre construït amb un icosaedre regular de nucli, enganxant 20 tetraedres a les cares |
|---|---|---|---|---|
| 12 triangles | 24 triangles | 60 triangles | ||
En lloc d'enganxar piràmides a les cares podem extreure-les com el següent exemple
 |
| Poliedre format a partir d'un dodecaedre del qual s'han extret de cada cara les piràmides |
|---|
| 60 triangles |
Referències
[modifica]- ↑ «Deltaedre IEC».
- ↑ «The Convex Deltahedra». [Consulta: 22 maig 2021].
- ↑ O. Rausenberger, Konvexe pseudoreguläre Polyeder. Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht 46(1915), 135 – 142. Jahrbuch über die Fortschritte der Mathematik 45, page 735.
- ↑ H. Freudenthal and B. L. van der Waerden, On an assertion of Euclid. (Dutch) Simon Stevin 25(1947), 115 – 121. Math Review 9, page 99c




